A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
√14πε0qQmR
√14πε0qQmR2
√14πε0qQmR3
√14πε0mqQ
The correct Answer is:C
To solve the problem of finding the angular frequency of a particle of mass m and charge −q moving diametrically through a uniformly charged sphere of radius R with total charge Q, we can follow these steps:
Step 1: Understand the System
We have a uniformly charged sphere of radius R with total charge Q. A particle with mass m and charge −q is moving through the sphere along its diameter.
Step 2: Determine the Electric Field Inside the Sphere
Using Gauss's law, the electric field E at a distance r from the center of a uniformly charged sphere (for r<R) is given by:
E=Q4πϵ0⋅rR3
This shows that the electric field inside the sphere is linearly proportional to the distance r from the center.
Step 3: Calculate the Force on the Particle
The force F acting on the particle due to the electric field is given by:
F=qE
Substituting the expression for E:
F=−q⋅(Q4πϵ0⋅rR3)
This simplifies to:
F=−qQ4πϵ0R3r
Step 4: Recognize the Form of Simple Harmonic Motion
The force can be rewritten in the form:
F=−kr
where k=qQ4πϵ0R3. This indicates that the particle is undergoing simple harmonic motion (SHM) about the center of the sphere.
Step 5: Relate the Force Constant to Angular Frequency
For SHM, the relationship between the force constant k and the angular frequency ω is given by:
F=−mω2r
Setting the two expressions for F equal gives:
−qQ4πϵ0R3r=−mω2r
Step 6: Solve for Angular Frequency
By equating the coefficients of r:
qQ4πϵ0R3=mω2
Rearranging gives:
ω2=qQ4πϵ0mR3
Taking the square root yields:
ω=√qQ4πϵ0mR3
Final Answer
Thus, the angular frequency of the particle's simple harmonic motion is:
ω=√qQ4πϵ0mR3
---
We have a uniformly charged sphere of radius R with total charge Q. A particle with mass m and charge −q is moving through the sphere along its diameter.
Using Gauss's law, the electric field E at a distance r from the center of a uniformly charged sphere (for r<R) is given by:
The force F acting on the particle due to the electric field is given by:
The force can be rewritten in the form:
For SHM, the relationship between the force constant k and the angular frequency ω is given by:
By equating the coefficients of r:
Thus, the angular frequency of the particle's simple harmonic motion is:
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Comprehension
Explore 25 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View Solution
Knowledge Check
A particle of mass m and charge q travels from rest through a potential difference V. Its final energy is
Aq VBmq VCq V/mDmq/VA particle of mass 'm' and charge 'q' is accelerated through a potential difference of V volt, its energy will be
AqVBmqVC(qm)VDqmVA particle of mass 'm' and charge 'q' is accelerated through a potential difference of V volt, its energy will be
AqVBmqVC(qm)VDqmV
A charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
View SolutionA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
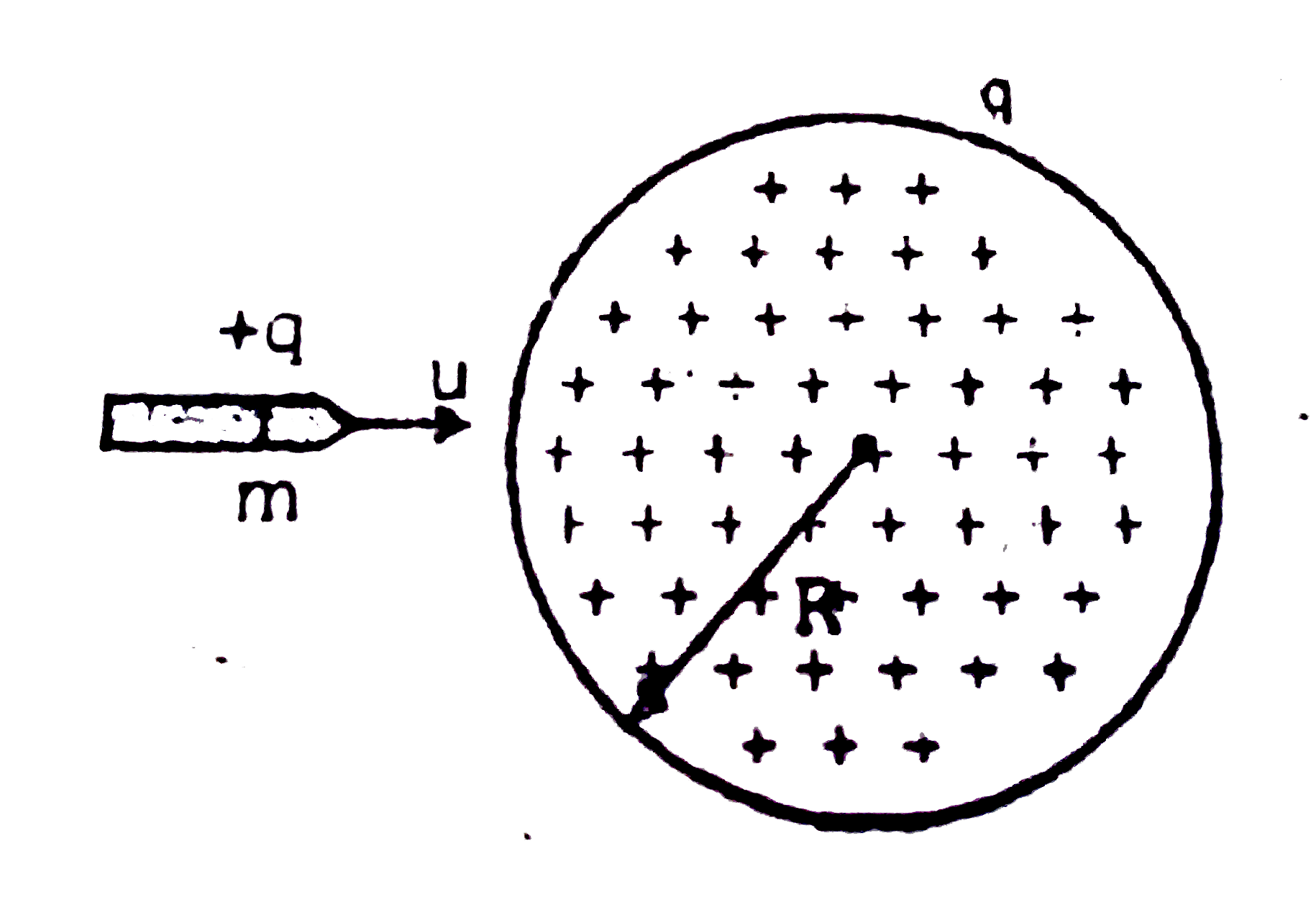
View SolutionA particle A of mass m and charge Q moves directly towards a fixed particle B, which has charge Q. The speed of A is a v when it is far away from B. The minimum separtion between the particles is not proportional to
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a unifrom magnetic fiels of strenght b the frequency of revolution is
View SolutionA metallic sphere of radius R having charge Q is connected to an uncharged sphere of radius 3R. The amount of charge flown through connecting wire is
View Solution