A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
The correct Answer is:12π√qQ4πɛ0mR3
F=qE
FR=−qQ4π∈0R3.x

FR=−Q4∈0R3x compare whith FR=−Kx and
put in n12π√Km
n=12π√Qq4π∈0R3m .
Similar Questions
A charge particle of charge q & mass m is projected towards the center of uniformly charged ring of radius R& carrying a charge Qfrom a distance of √3R from the center along the axis,find the minimum value of velocity of projection (in ms ) so that particle reaches to x=−∞ where x - axis is along the axis of ring & center of ring is at origin.(given Q=6μc,q=3μc,m= 2gm,R=1m )
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View Solution
Knowledge Check
A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
A√14πε0qQmRB√14πε0qQmR2C√14πε0qQmR3D√14πε0mqQA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
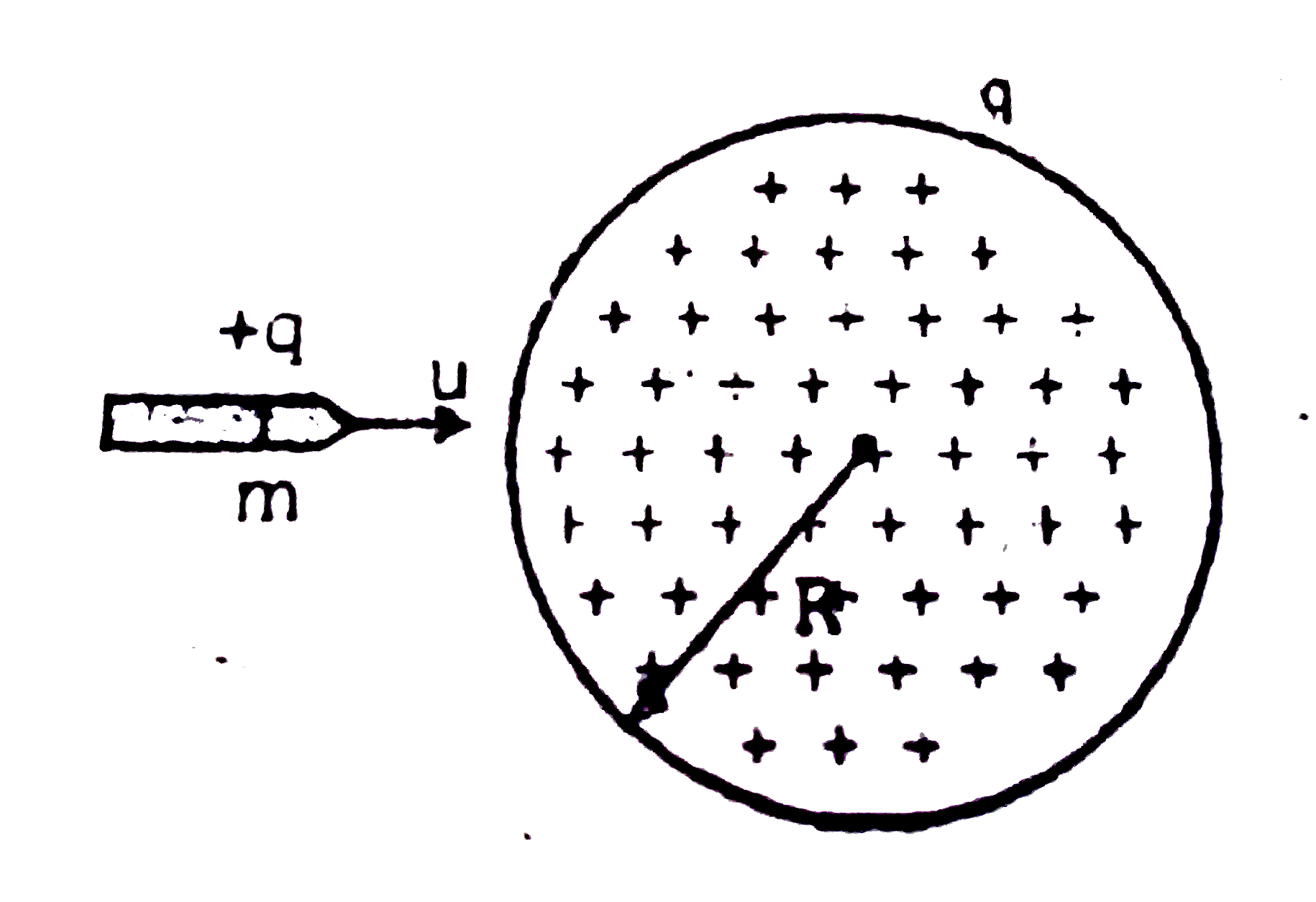 Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mR
Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mRA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of these
A particle of mass 1 mg and charge q is lying at the mid-point of two stationary particles kept at a distance '2 m' when each is carrying same charge 'q'. If the free charged particle is displaced from its equilibrium position through distance 'x' (x<<1 m). The particle executes SHM. Its angular frequency of oscillation will be __________ ×105 rad/s if q2=10C2
View SolutionA charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionA particle having charge + q is fixed at a point O and a second particle of mass m and having charge −q0 moves with constant speed in a circle of radius r about the charge +q. the energy required to be supplied to the moving charge to increase radius of the path to 2r is qq0nπε0r. Find the value of n.
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View Solution
