A particle A of mass m and charge Q moves directly towards a fixed particle B, which has charge Q. The speed of A is a v when it is far away from B. The minimum separtion between the particles is not proportional to
Q2
1v2
1v
1m
The correct Answer is:C
12mv2=14πε0Q2rmin or rmin.=2Q3(4πε0)mv2
Clearly rmin∝Q2∝1m∝1v2
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section B - Assertion Reasoning
17 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIPMTNEET Questions
38 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor Circuits
52 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A uniformly charged sphere has radius R and charge Q on it. A negatively charged particle having mass m and charge – q shoots out of the surface of the sphere with speed V. The minimum speed (V0) for which the particle escapes the attraction of the sphere may be called as escape speed. Will the value of V0 depend on magnitude of q? [Recall that escape speed of a body from the surface of the earth does not depend on its mass].
View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View Solution
Knowledge Check
A particle of mass m and charge q travels from rest through a potential difference V. Its final energy is
Aq VBmq VCq V/mDmq/VA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
AAways circularBcircular, If v×B=0Ccircular,If v.B=0DNone of theseA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/Bq
A charged particle +q of mass m is placed at a distance d from another charge particle −2q of mass 2m in a uniform magnetic field of induction vectro B as shown in the fig.If the particles are projected towards each other with equal speeds v.(Neglect the interaction between the particles)
(a)Find the maximum value of the projection speed Vmax so that the two particles do not collide.
b)Find the time interval after which collision occurs between the particles if projection speed equals 2Vmax
(c)In the previous part,assuming that the particles stick after the collision find the radius of the circular path of the particle in subsequent motion.

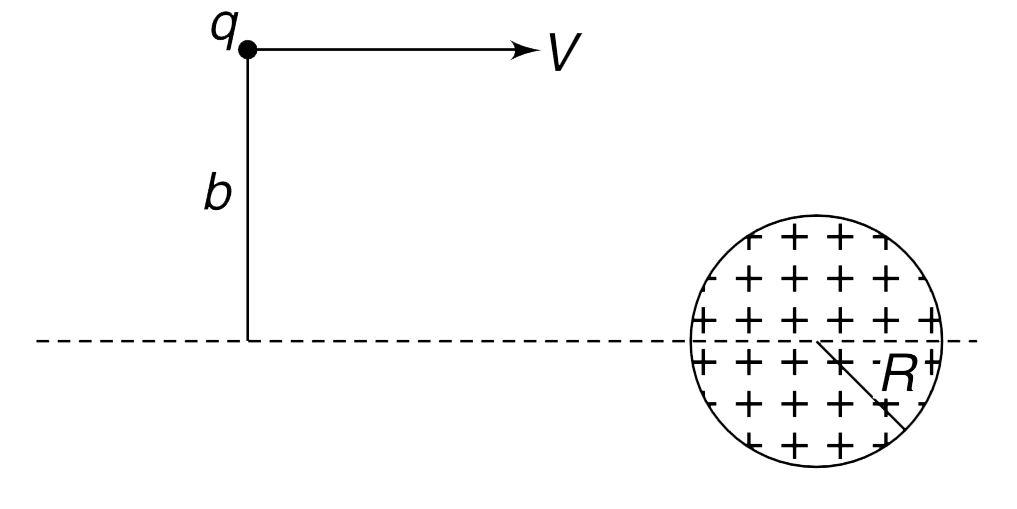
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionA particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
View SolutionA particle of charges Q and mass m travels through a potential difference V from rest. The final momentum of the particle is
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View Solution
