A basket ball of radius is spun with an angular. and its moves with a speed . Find aerodynamic lift experienced by the ball. Assume density of air.
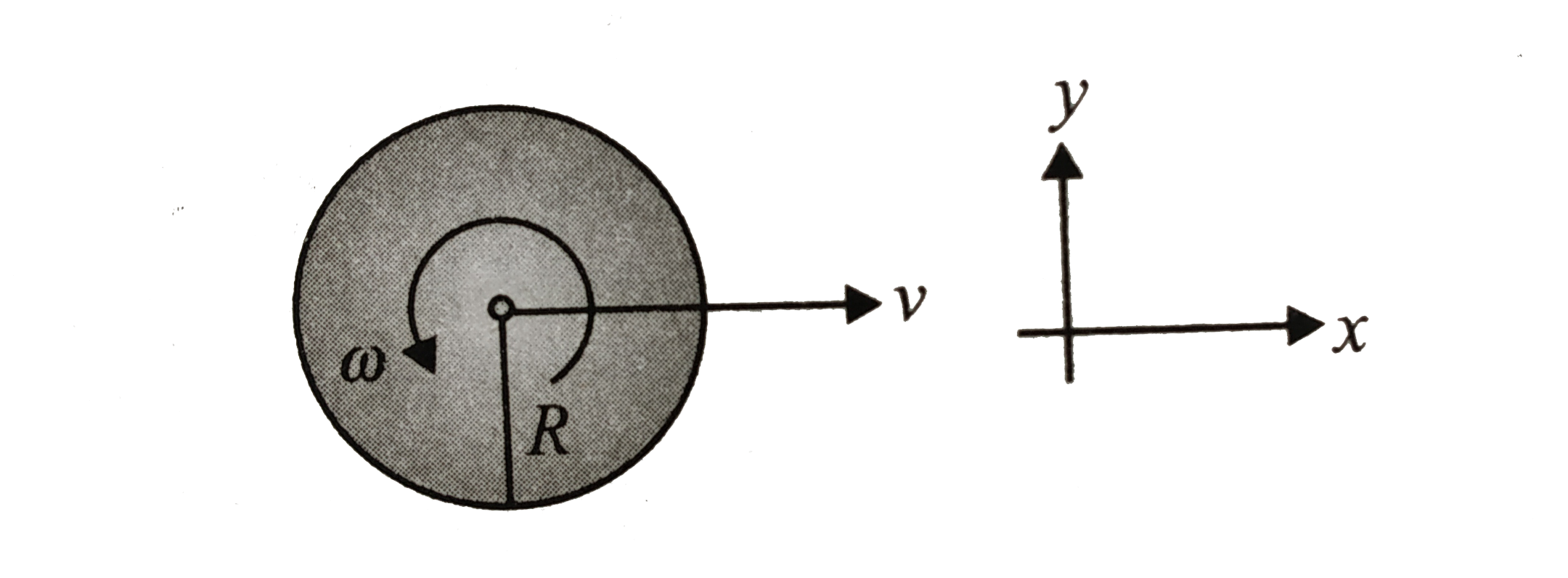
The correct Answer is:
where and
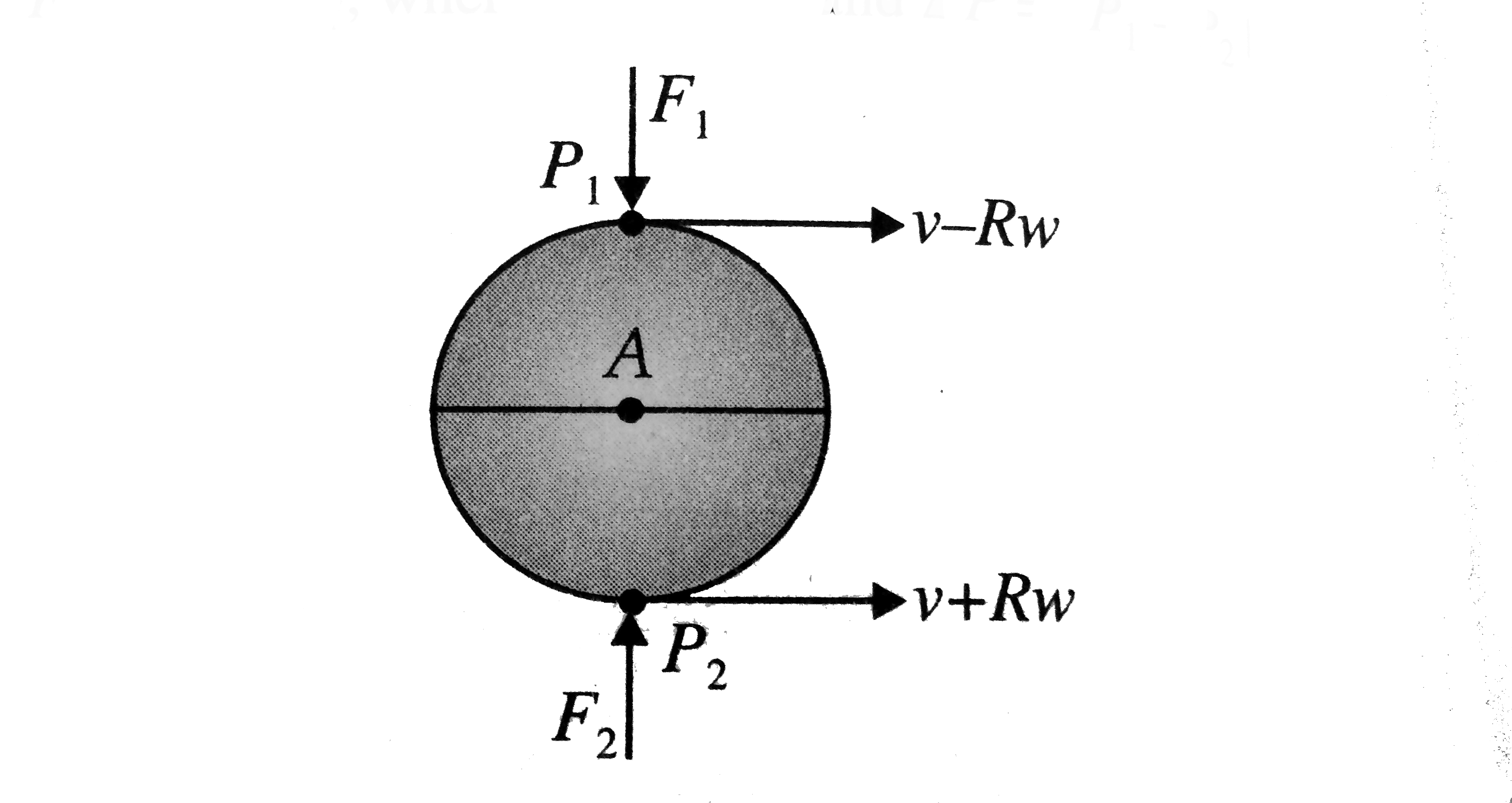
Then
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.4
Explore 10 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A ball of radius r hits a cushion with a pure rolling motion and rebounds, with a pure rolling motion. Find the ratio of the height h of the cushion to the radius r of the ball. Assume that the foce exerted on the ball by the cushion is horizontal during the impact and that the ball hits the cushion normally.
View SolutionA ball of mass m is projected vertically up from a smooth horizontal floor with a speed v. Find the total momentum delivered by the ball to the surface during impact assuming e as the cofficient of restitution of impact.

View Solution
Knowledge Check
A copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
A1.2×10−2JB2.4×10−2JC3.6×10−2JD4.8×10−2JA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsin.ωt2A particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsinωt2
A small charged ball is in state of equilibrium at a height h above a large horizontal uniformly charged dielectric plate having surface charge density of σC/m2. (a) Find the acceleration of the ball if a disc of radius r (ltlt h) is removed from the plate directly underneath the ball. (b) Find the terminal speed (V0) acquired by the falling ball. Assume that mass of the ball is m, its radius is x and coefficient of viscosity of air is η. Neglect buoyancy and assume that the ball acquires terminal speed within a short distance of its fall.
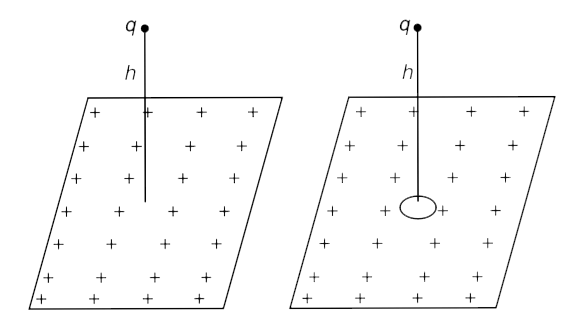
View SolutionA massive ball moving with speed v collides with a tiny ball by negligible mass. The collision is elastic. Find the speed with which the second tiny ball will move.
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View SolutionA ball of mass m is thrown in air with speed v1 from a height h1 and it is at a height h2(>h1) when its speed becomes v2 . Find the work done on the ball the air resistance.
View SolutionA ball of mass m moving with speed v towards the right strikes a wall moving towards the left with speed u. Find the change in the K.E. of the ball if the collision is elastic.
View Solution

