A cup ABC is kept in a liquid of density ρ as shown in the figure. Find the vertical thrust on the cup by the liquid present in region 2, if the maximum volume of the liquid that can be kept in the cup is equal to V.
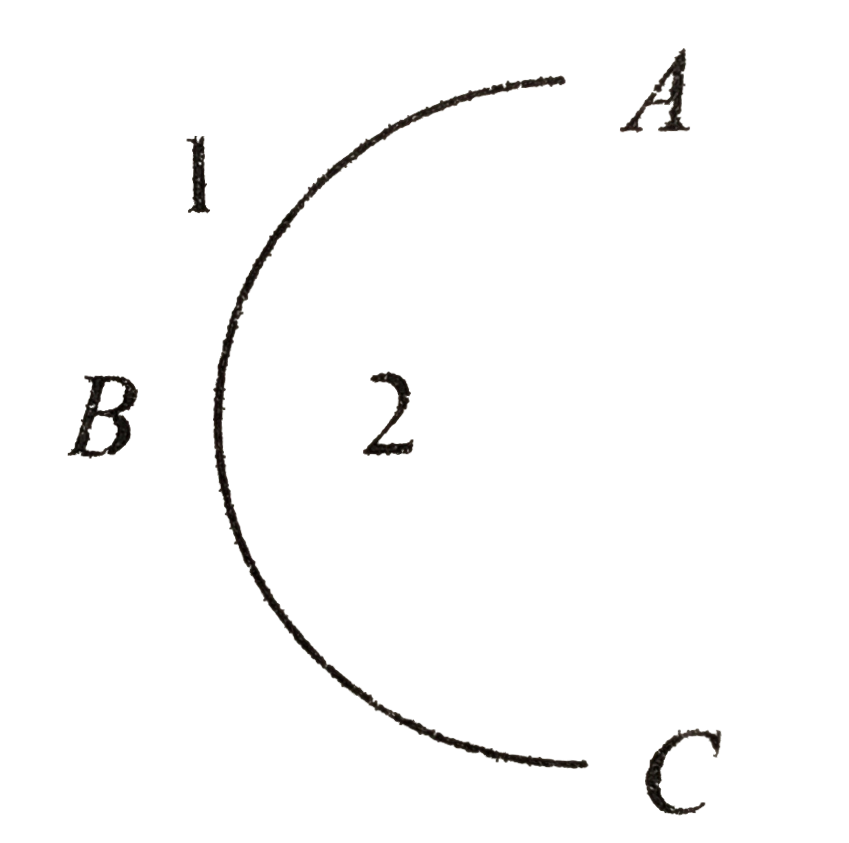
The correct Answer is:Vρg
Let us divide the cup into two parts AB and BC. Liquid pushes the curved surface AB upwards and BC downwards.
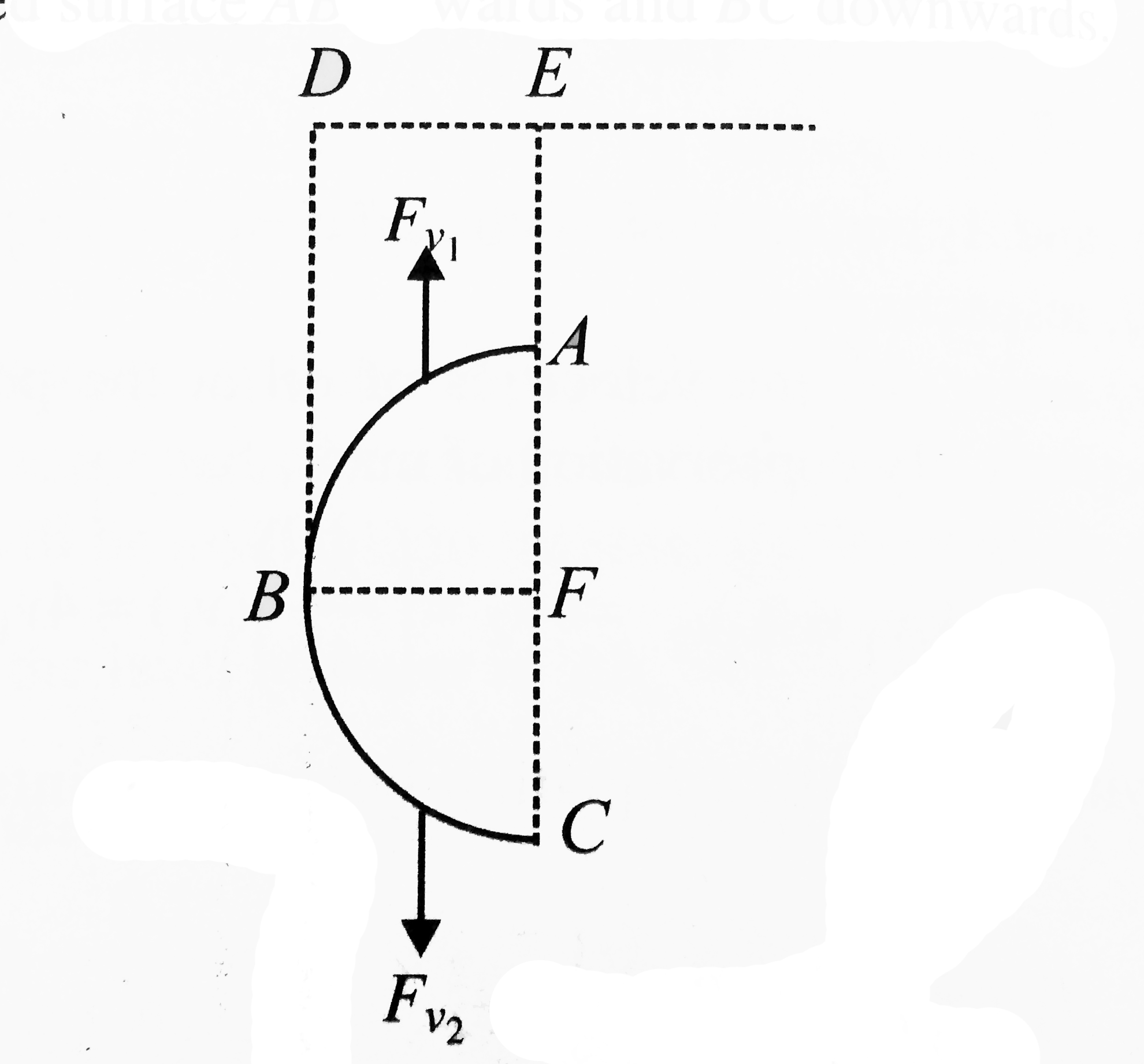
Vertical of the liquid on AB is Fv1=V1ρg
where V1= volume of the portion ABDE above AB similarly, the vertical thrust of liquid on BC is Fv2=V2ρg where V2= volume of the potion ABCDE above BC.
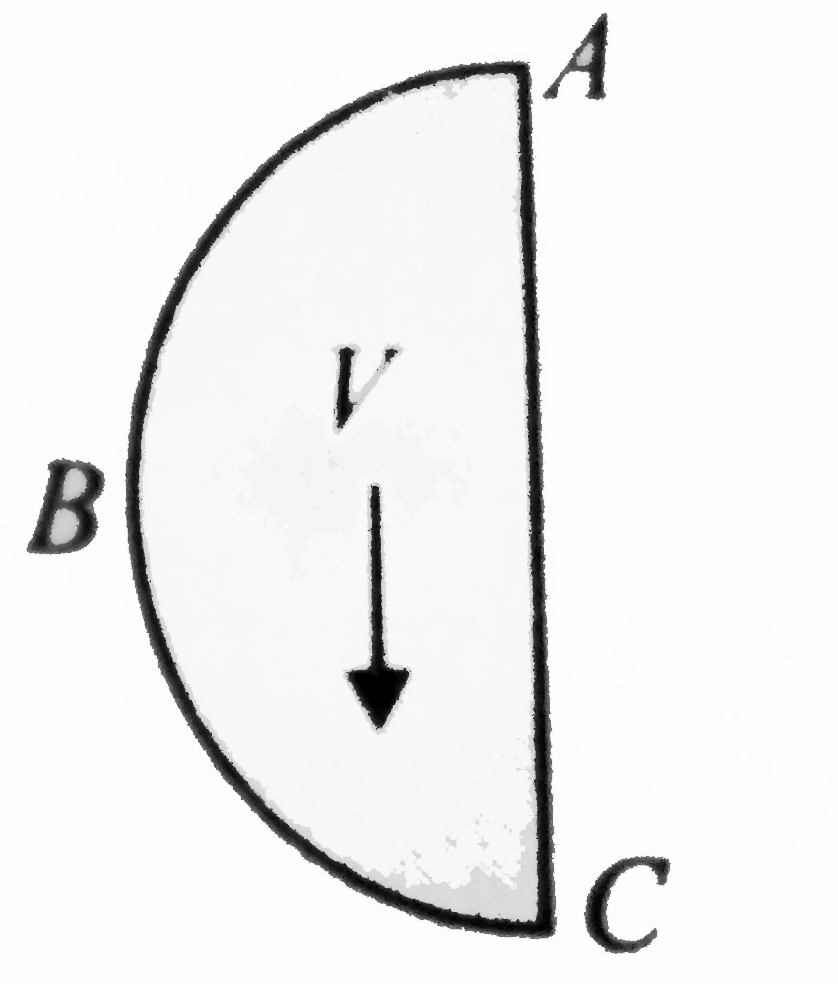
Hence the net vertical force on the curved surface ABC of the cup is Fv=Fv2=Fv1=V2ρg−V1ρg=(V2−V1)ρg=Vρg
Where V= volume of liquid in the cup shown as shaded portion.
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.4
Explore 10 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
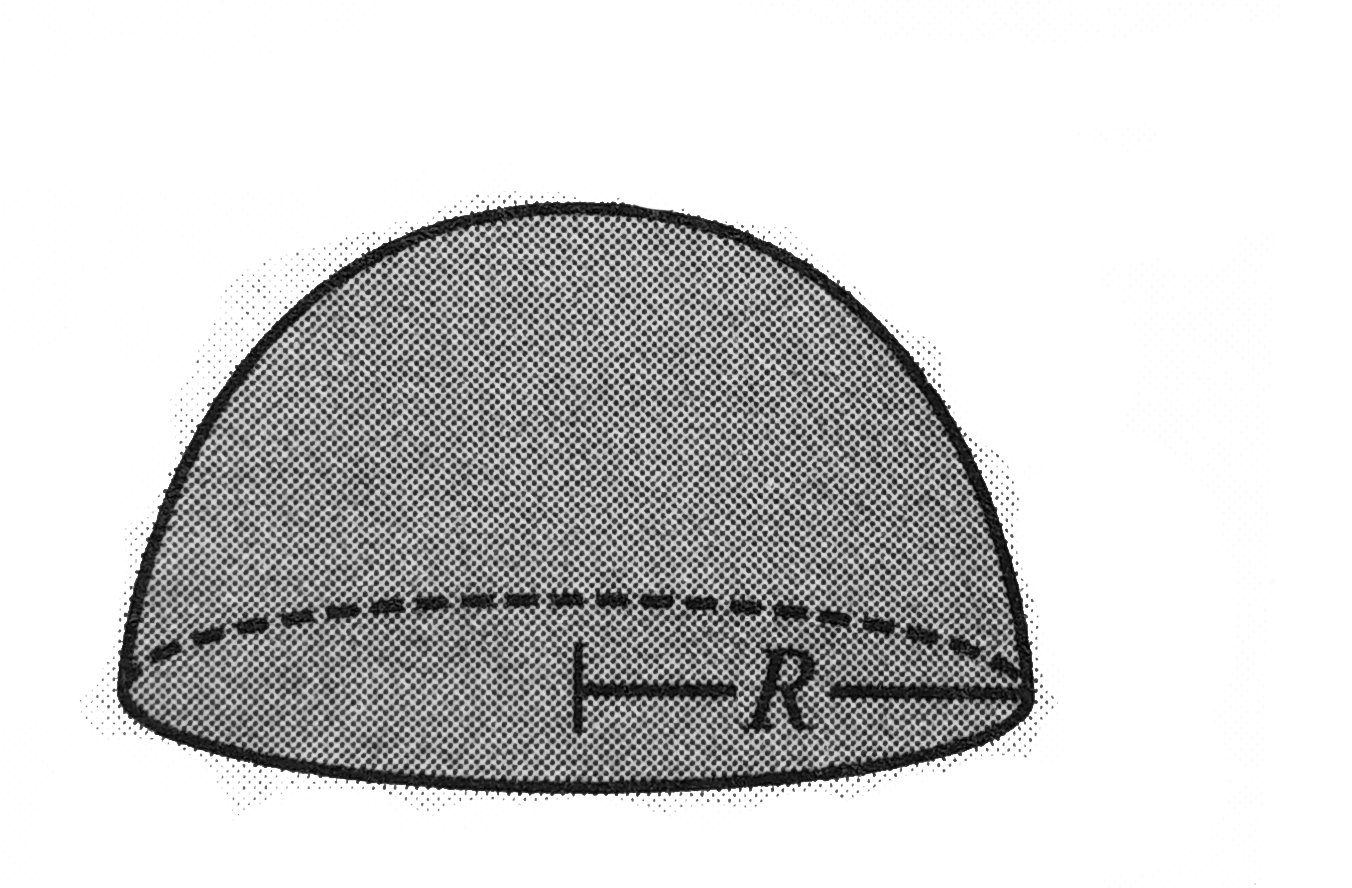
A solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View Solution
Knowledge Check
A solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
AdDBDdCDD+dDD+dDTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
A2ρ3Bρ2C8ρ5D4ρ5A vertical U-tube contains a liquid of densityρ and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are R1 and R2 find the difference in the liquid column in the limbs.
AΔh=T(R1−R2)ρgR1R2BΔh=2T(R1−R2)ρgR1R2CΔh=2T(R1+R2)ρgR1R2DΔh=4T(R1−R2)ρgR1R2
A liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
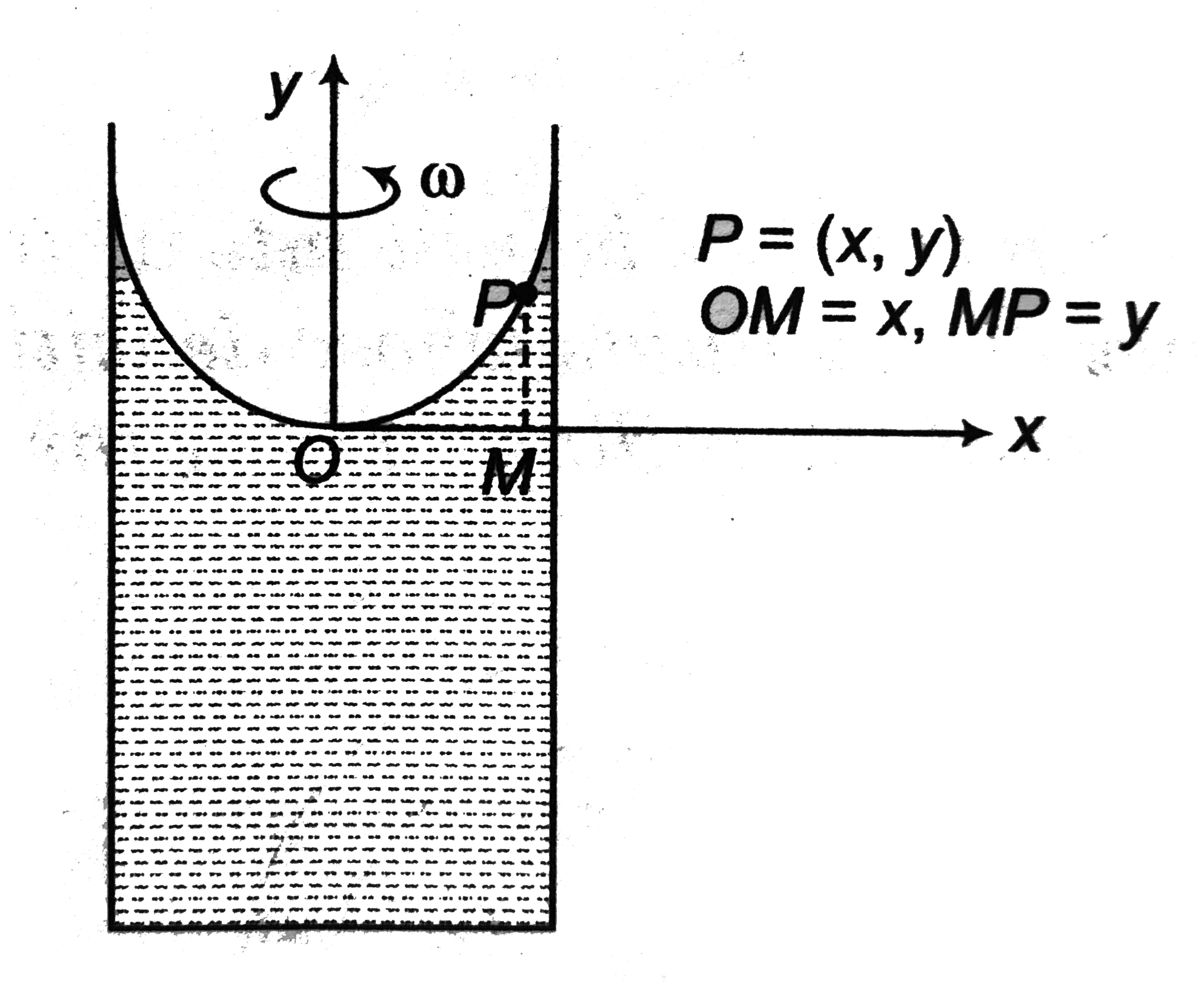 .
.
View SolutionA liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
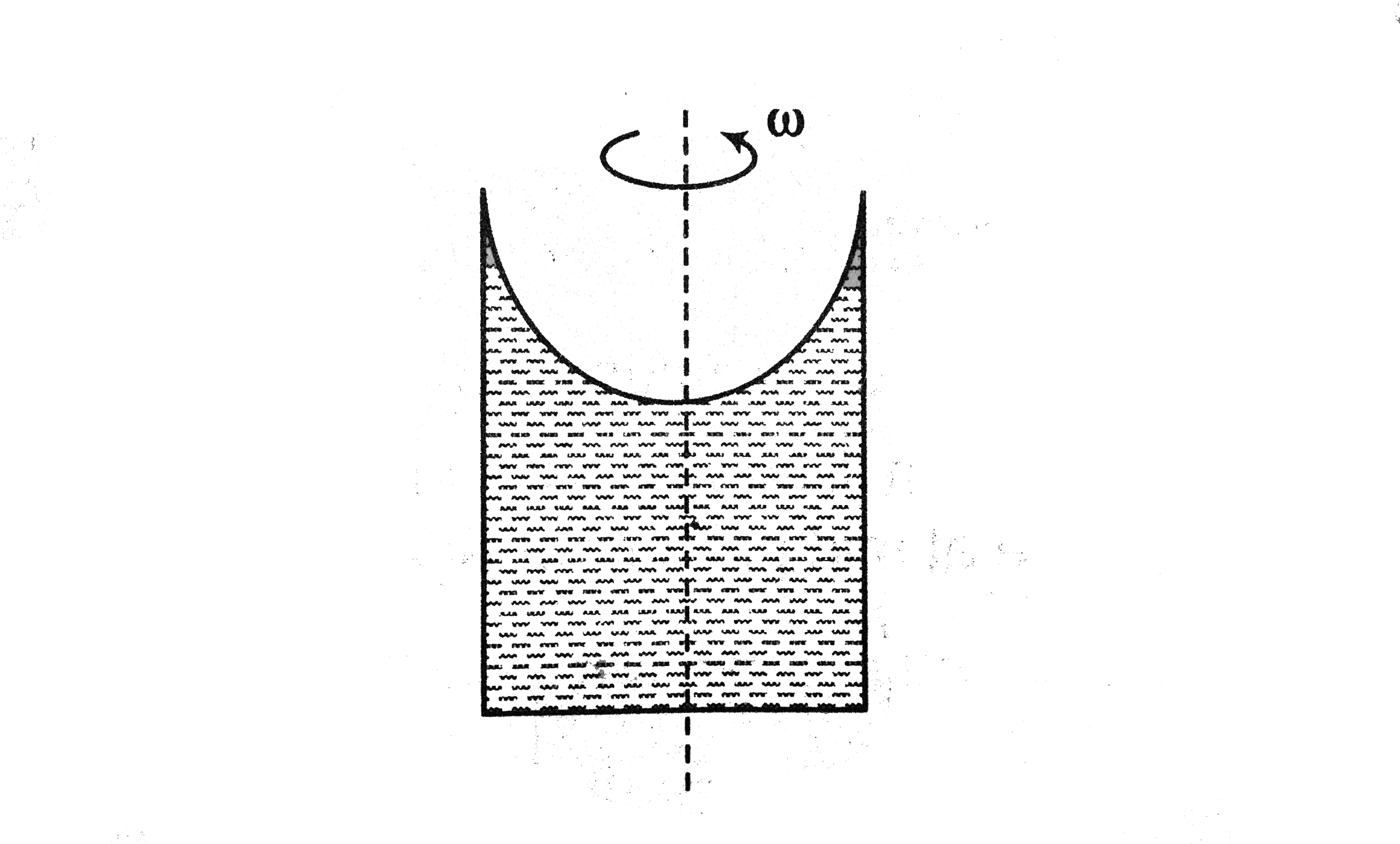 .
.
View SolutionA solid of density D is floating in a liquid of density d. If v is the volume of solid submerged in the liquid and V is the total volume of the solid, then (v)/(V) is equal to
View SolutionA solid of density D is floating in a liquid of density d. If V is the volume of solid submerged in the liquid and V is the total volume of the solid, then V/V is equal to
View Solution_E01_052_Q01.png)
An object of volume V is submerged in a liquid of density ρ. It has flat bottom of area A which is at depth of H in the liquid and a dome shaped top find the total force of liquid acting on the top of the object.
View Solution

