A vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

The correct Answer is:ρgh4
dpdx=ρ(ω2x)⇒dp=ρω2xdx
integrating both sides, we get

∫p3p1dp=ρω2∫2h−hxdx
p3−p1=ρω2[x22]=ρω22[4h2−h2]
ρ(h3−h1)=3ρω2h22=3ρ2h2(gh)
h3=h1=3h2..........i
But h3+h1=2h.........ii
After solving h3=7h4 and h1=h4
p3=p0+rog(7h4) and p1=p0+ρg(h4)
and p3−p2=ρω22[x2]20=ρω22(rh)2
p3−p2=ρ2(gh).4h2=2ρgh
p0+ρg(7h4)−p2=2ρgh⇒p2=p0−ρgh4
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.4
Explore 10 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
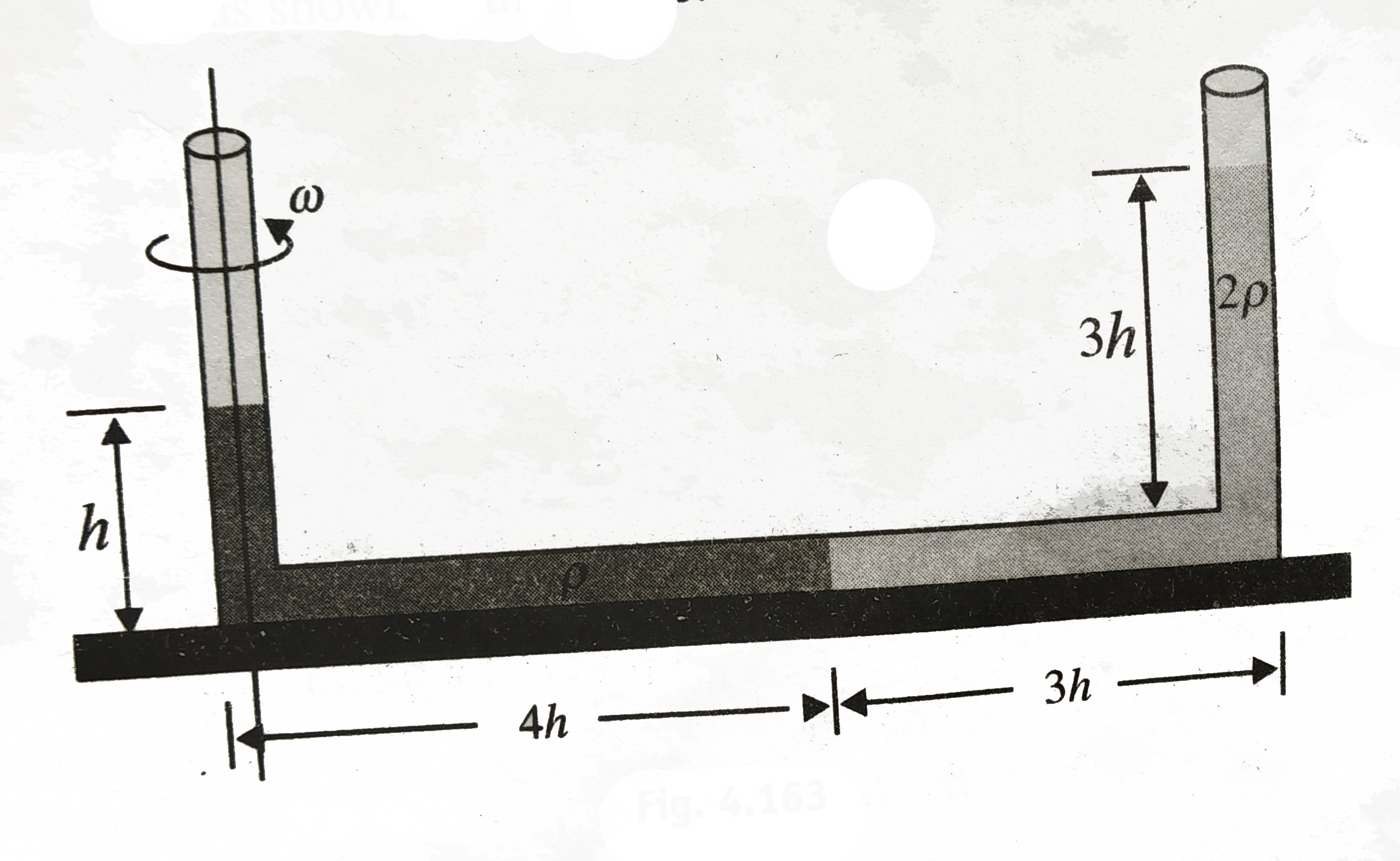
View SolutionWhen a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is

View Solution
Knowledge Check
The formula for height of a liquid column (h) in a capillary tube is
Ah=2TrpgBh=2TcosθrpgCh=2TsinθrpgDh=T2cosθrpgA vertical U-tube contains a liquid of densityρ and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are R1 and R2 find the difference in the liquid column in the limbs.
AΔh=T(R1−R2)ρgR1R2BΔh=2T(R1−R2)ρgR1R2CΔh=2T(R1+R2)ρgR1R2DΔh=4T(R1−R2)ρgR1R2The rise of liquid into capillary tube is h1. If the apparatus is taken in a lift moving up with acceleration the height is h2 then
Ah1=h2Bh1>h2Ch2>h1Dh2=0

A liquid of density ρ is rotated by an angular speed ω as shown in figure, Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.
View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
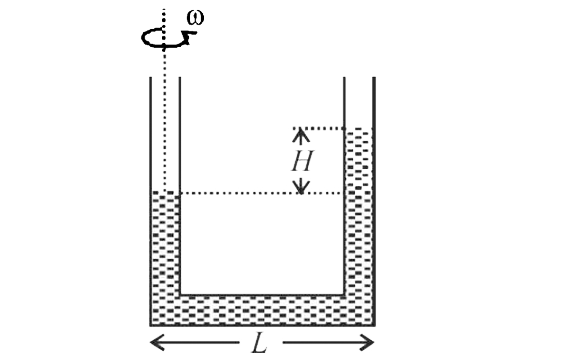
View Solution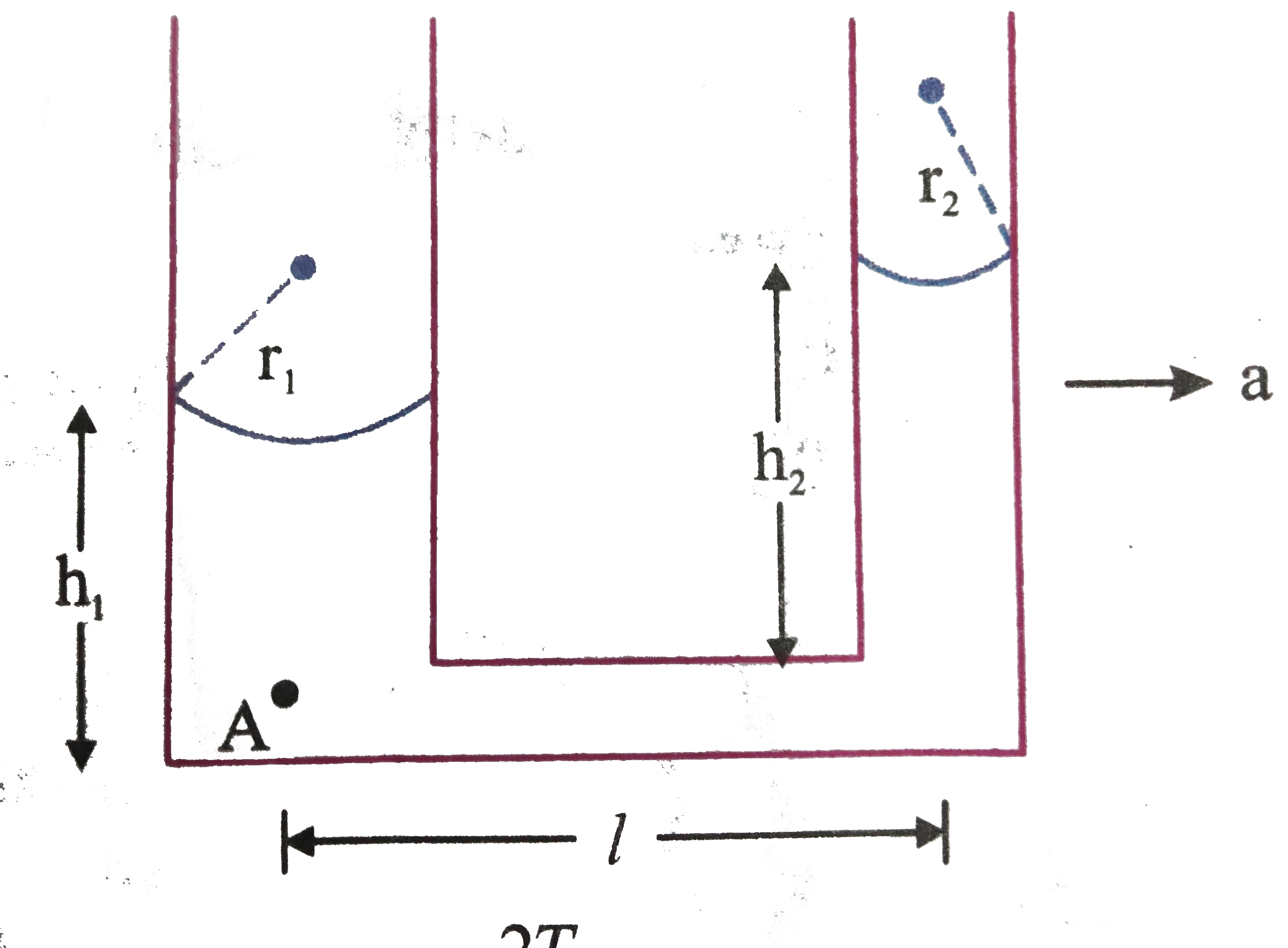
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :
View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
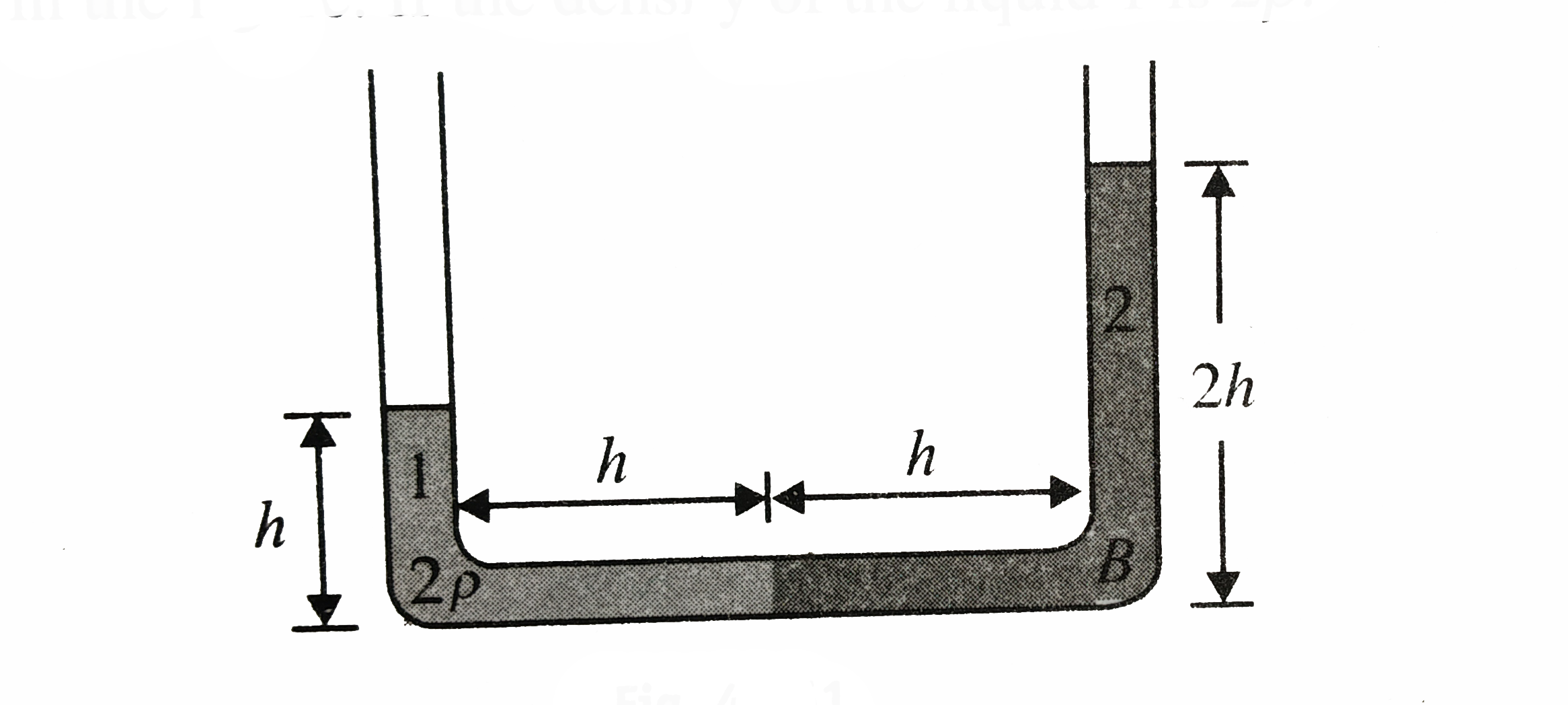
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View Solution

