A wooden stick of length L, radius R and density ρ has a small metal piece of mass m ( of negligible volume) atached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density σ(>ρ).
To solve the problem of finding the minimum mass m that will allow the wooden stick to float vertically in equilibrium in a liquid of density σ, we can follow these steps:
Step 1: Calculate the Volume of the Wooden Stick
The volume V of the wooden stick can be calculated using the formula for the volume of a cylinder:
V=πR2L
where R is the radius and L is the length of the stick.
Step 2: Calculate the Weight of the Wooden Stick
The weight Wstick of the wooden stick can be calculated using its volume and density:
Wstick=V⋅ρ=πR2L⋅ρ
Step 3: Calculate the Weight of the Metal Piece
The weight Wm of the metal piece is given by:
Wm=m⋅g
where m is the mass of the metal piece and g is the acceleration due to gravity.
Step 4: Calculate the Buoyant Force
The buoyant force Fb acting on the stick when it is submerged in the liquid is equal to the weight of the liquid displaced by the stick:
Fb=Vdisplaced⋅σ⋅g=πR2L⋅σ⋅g
Step 5: Set Up the Equilibrium Condition
For the stick to float in equilibrium, the total weight acting downwards must equal the buoyant force acting upwards:
Wstick+Wm=Fb
Substituting the expressions from Steps 2, 3, and 4 into this equation gives:
πR2L⋅ρ+m⋅g=πR2L⋅σ⋅g
Step 6: Solve for the Mass m
Rearranging the equation to solve for m:
m⋅g=πR2L⋅σ⋅g−πR2L⋅ρ
m=πR2L⋅(σ−ρ)g
Final Expression for Minimum Mass m
Thus, the minimum mass m required to make the stick float vertically in equilibrium is:
m=πR2L⋅(σ−ρ)g
The volume V of the wooden stick can be calculated using the formula for the volume of a cylinder:
V=πR2L
where R is the radius and L is the length of the stick.
The weight Wstick of the wooden stick can be calculated using its volume and density:
Wstick=V⋅ρ=πR2L⋅ρ
The weight Wm of the metal piece is given by:
Wm=m⋅g
where m is the mass of the metal piece and g is the acceleration due to gravity.
The buoyant force Fb acting on the stick when it is submerged in the liquid is equal to the weight of the liquid displaced by the stick:
Fb=Vdisplaced⋅σ⋅g=πR2L⋅σ⋅g
For the stick to float in equilibrium, the total weight acting downwards must equal the buoyant force acting upwards:
Wstick+Wm=Fb
Substituting the expressions from Steps 2, 3, and 4 into this equation gives:
πR2L⋅ρ+m⋅g=πR2L⋅σ⋅g
Rearranging the equation to solve for m:
m⋅g=πR2L⋅σ⋅g−πR2L⋅ρ
m=πR2L⋅(σ−ρ)g
Thus, the minimum mass m required to make the stick float vertically in equilibrium is:
m=πR2L⋅(σ−ρ)g
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.2
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionTwo non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View Solution
Knowledge Check
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
A(a) The net elongation of the spring is 4πR3ρg3kB(b) The net elongation of the spring is 8πRρg3kC(c) The light sphere is partially submergedD(d) The light sphere is completely submergedA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
A√2σπρlgB√2σlπρgC√σπρgD√2σπρgA wooden block or mass m and density ρ is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density σ with σ>ρ. The tension in the string will be
A(σ−ρσ)mgB(σ−ρρ)mgCρmgσDσmgρ
A mass m is taken to a height R from the surface of the earth and then is given a vertical velocity υ. Find the minimum value of υ, so that mass never returns to the surface of the earth. (Radius of earth is R and mass of the earth m).
View SolutionTwo non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________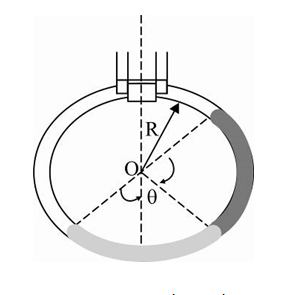
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionThere is an insulator rod of length L and of negligible mass with two small balls of mass m and electric charge Q attached to its ends. The rod can rotate in the horizontal plane around a vertical axis crossing it at a L/4 distance from one of its ends.
What is the time period of the SHM as mentioned in previous question?
View Solution

