A container of large uniform cross sectonal area A, resting on horizontal surface, holds two immiscible non viscous and incompresible liquids of density d and 2d, each of height H2 as shown in the figure. Thelower density liquid is open to the atmospher having presure P0. A tiny hole of area (s(s>>A) is punched on the vertical side of the container at a height h(h>H2). Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance x travelled by the liquid initially
c. the height hm at which at the hole should be punched so that the liquid travels the maximum distance xm initially. also calculate xm (neglect air resistance inte calculations).
a. Applying Beroulli's theorem at point E ( a point on the interface of the liquids and on the top surface of the liquid of density 2d) and F, i.e, pressure energy = kinetic energy + potential energy = constant
⇒P0+H2dg+12(2d)×0+H2dg
=P0+12(2d)v2+2hdg
⇒32Hdg=dv2+2hdg
⇒v2=32Hg−2hg=(3H−4h)g2
∴v=
⎷{(3H−3h)2g}
Method :2 Let the equivalent depth of liquid 1 of denisty in terms of density 2d which gives the dame pressure as liquid 1 at interface i.e.,
H2dg=H'(2d)g which gives H'=H4
Hence depth depth of the liquid above opening (in terms of depth of liquid of density 2d).
H'+(H2−h)=H4+(H2−h)
Hnet=(3H−4h4)
and velocity of efflux is given by
v=√2ghnet
v=√3H−4h2g
time taken by the liquid to fall through a vertical height h is given by
H=12gt2⇒t=√2hg
Therefore horizontal distance traversed by liquid is
x=vt=√(3H−4h)g2×√2hg
c. For the minimum horizontal distance x
dxdh=0⇒ddh(3Hh−4h2)12=0
or 1293Hh−4h2^(−12)×(3H−8h)=0
this gives 3H−8h−0⇒h=3H8
This is the length of the liquid for which the range is maximum i.e
h→hm=3H8
The maximum horizontal distance is given by
xm=√(3H−3hm)hm
√{(3H−43H3)3H8}9=34H
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.1
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Exercise 4.2
Explore 11 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
What is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
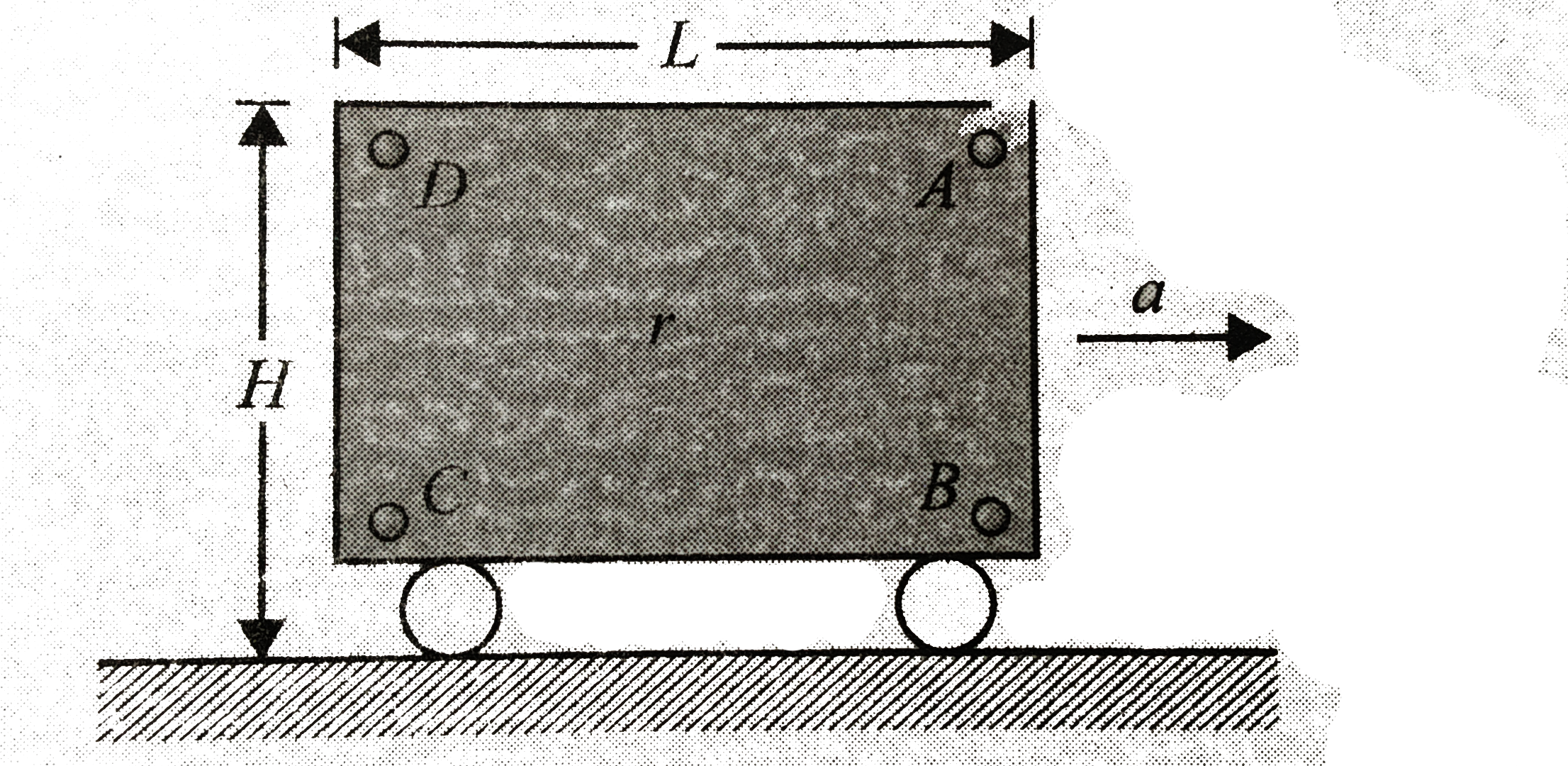
View SolutionA rectangular box is completely filled with a liquid of density ρ, as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points A,B,C and D.
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionGravitational acceleration on the surface of the planet is √611g. where g is the gravitational acceleration on the surface of the earth. The average mass density of the planet is 23 times that of the earth. If the escape speed on the surface of the earth is taken to be 11kms−1 the escape speed on the surface of the planet in kms−1 will be
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure P_o . A tiny hole of area a (a lt lt A) is punched on the vertical side of the lower container at a height h (0 lt h lt H/2) for which range is maximum.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionA container of large uniform cross sectonal area A, resting on horizontal surface, holds two immiscible non viscous and incompresible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance x travelled by the liquid initially
c. the height hm at which at the hole should be punched so that the liquid travels the maximum distance xm initially. also calculate xm (neglect air resistance inte calculations).
View SolutionA container of large uniform cross sectional area A , resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d , each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A tiny hole of area (s(sltltA) is punched on the vertical side of the container at a height h(hltH/2) . Determine The horizontal distance traveled by the liquid, initially, is :
View Solution

