Two discs, each having mass m, are attached rigidly to the ends of a vertical spring. One of the discs rests on a horizontal surface and the other produces a compression x0 on the spring when it is in equilibrium. How much further must the spring be compressed so that when the force causing compression is removed, the extension of the spring will be able to lift the lower disc off the table?
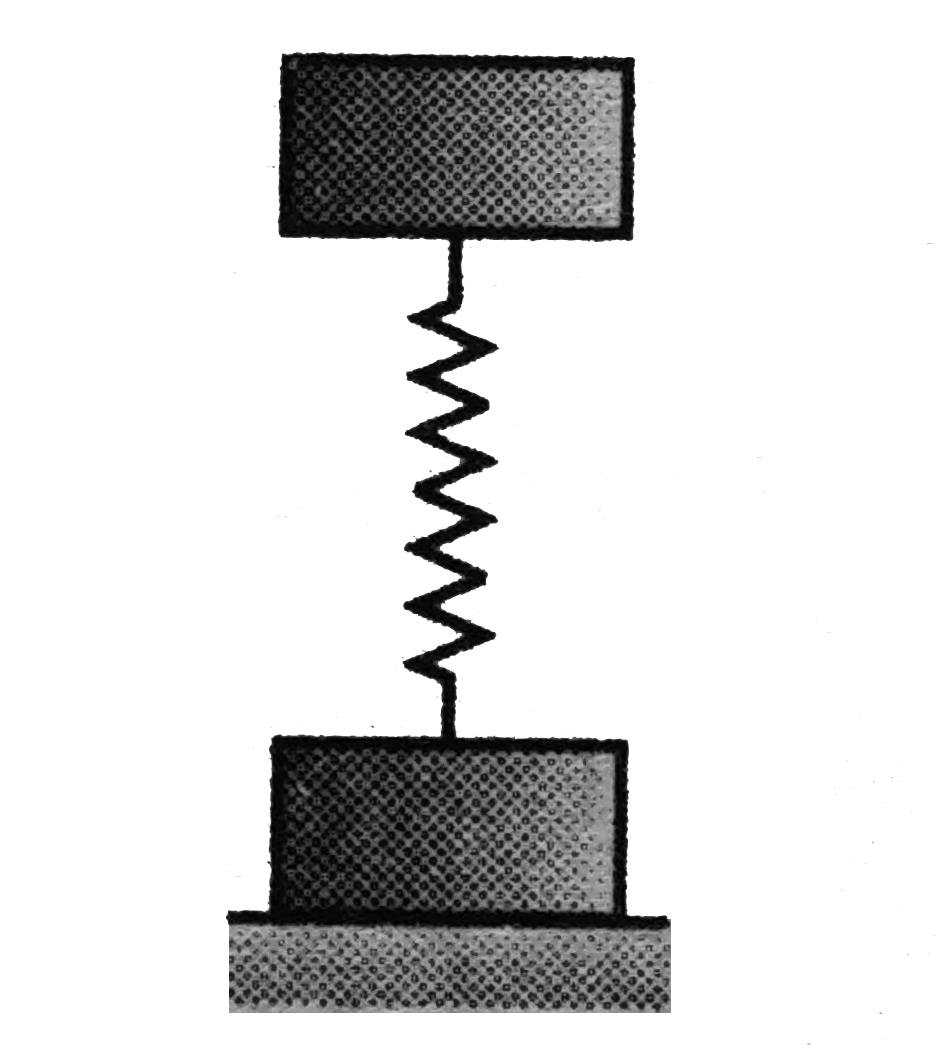
(a) x0
(b) 2x0
(c) 3x0
(d) 1.5x0
The correct Answer is:B
A is the position of the spring when it is in its normal uncompressed length. The upper disc compresses the spring by x0 when spring is in equilibrium. So kx0=mg. Hence, B is the equilibrium position of the spring. Let it be further compressed by y and released. After releasing it can be proved that the spring will go up to the position D so that BC=BD. Extension in the spring at this position
=y−x0.
Now for lifting up of the lowe disc:
k(y−x0)=mg⇒y=mgk+x0
⇒y=x0+x0=2x0

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
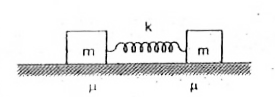
View Solution
Knowledge Check
Two plates of some mass are attached rigidly to the two ends of a spring as shown in figure. One of the two ends of a spring s shown in figure. One of the plates resets on a horizontal surface to the other rusults a compression y of the spring when it is in equilibrium state. The further minimum compression required, so that when the force causing compression is removed the lower plate is lifted off the surface, will be :
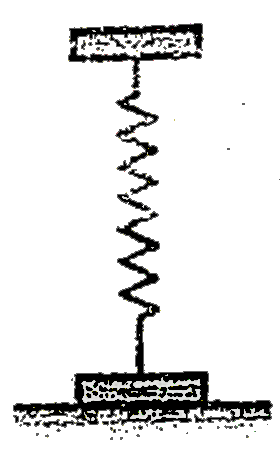 A0.5yB3yC2yDy
A0.5yB3yC2yDyWhen a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/mA compressed spring possesses :
AElectric energyBChemical energyCPotential energyDKinetic energy
The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
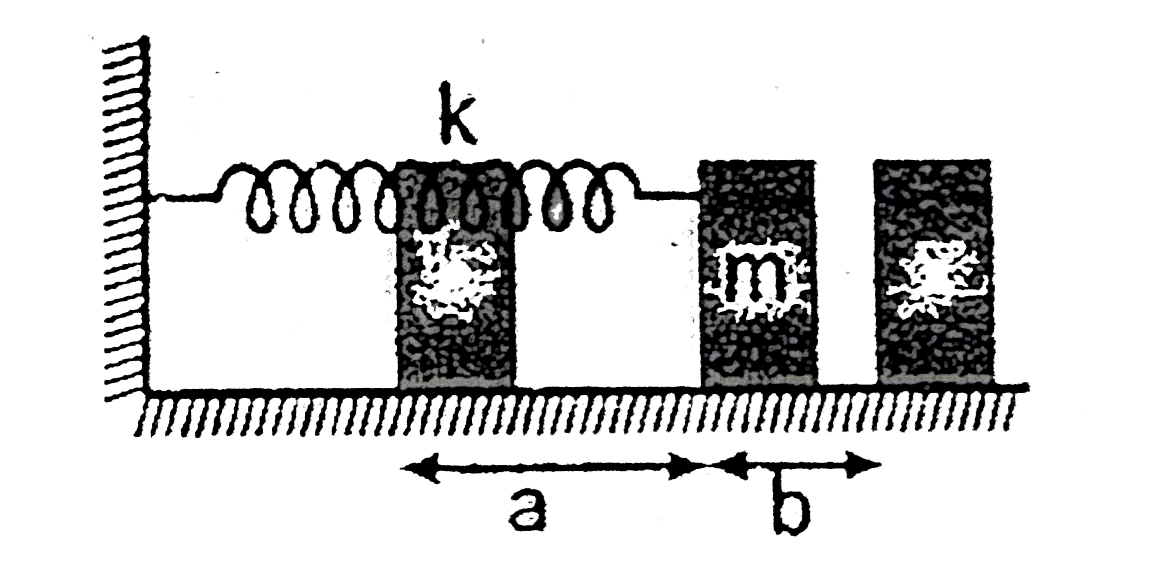
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionAll surfaces shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be

View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
View Solution

