In fig. man A is standing on a movable plank while man B is standing on a stationary platform. Both are pulling the string down such that the plank moves slowly up. As a result of this the string slops through the hands of the men, find the ratio of length of the string that slips through the hands of A and B.

3/2
3/4
4/3
2/3
The correct Answer is:C
Let the plank move up by x, then pulley 2 will move down by x. Let the end of string C moves down by a distance y.
Let the initial length of string passing over pulley 2,
l1+l2…(i)
After displacements x and y mentioned above, the lengths become
(l1−2x)+(l2+y−x) ..(ii)
Equating Eqs. (i) and (ii), we get y=3x
Length of string that slips through A is y+x=4x and through B is y=3x.
Required ratio=4x3x=43

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A string of negligible thicknes is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the sitting an pulls the cylinder towards him figure. There is no slipping anywhere. The length of the string passed through the hand of the man whicle the cylinder reaches his hands is

View SolutionA man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
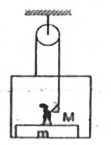
View Solution
Knowledge Check
A man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
A3L4BL4C4L5DL3A system consisting of a man on platfrom is in equilibrium. Masses of man and platiform are equal. The platform is in equilibrium due to two massless string is pulled by man resting on platform. Find the ratio of tension in left string to the tension in right string.
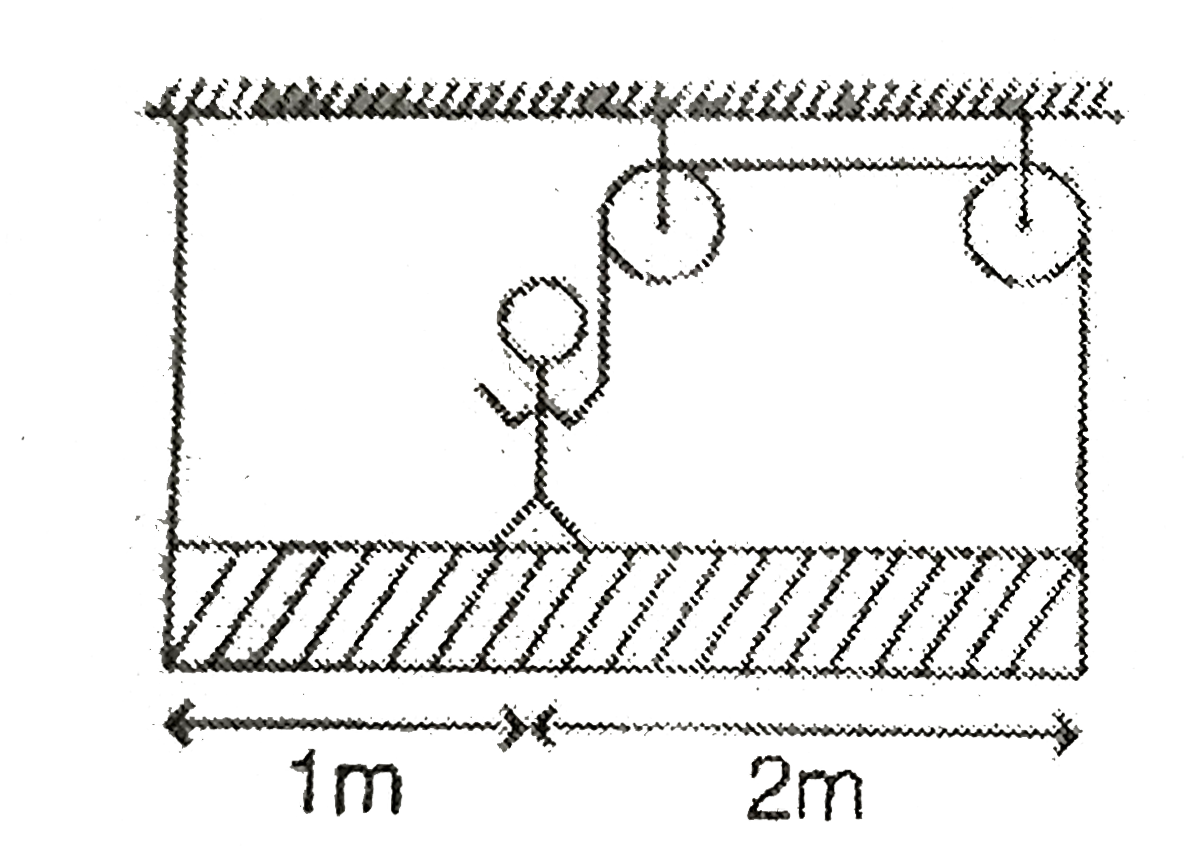 A5/6B4/3C6/5D3/4
A5/6B4/3C6/5D3/4A system is shown in the figure. A man standing on the block is pulling the rope. Velocity of the point of string in contact with the hand of the man is 2m/s downwards. The velocity of the block will be [assume that the block does not rotate]
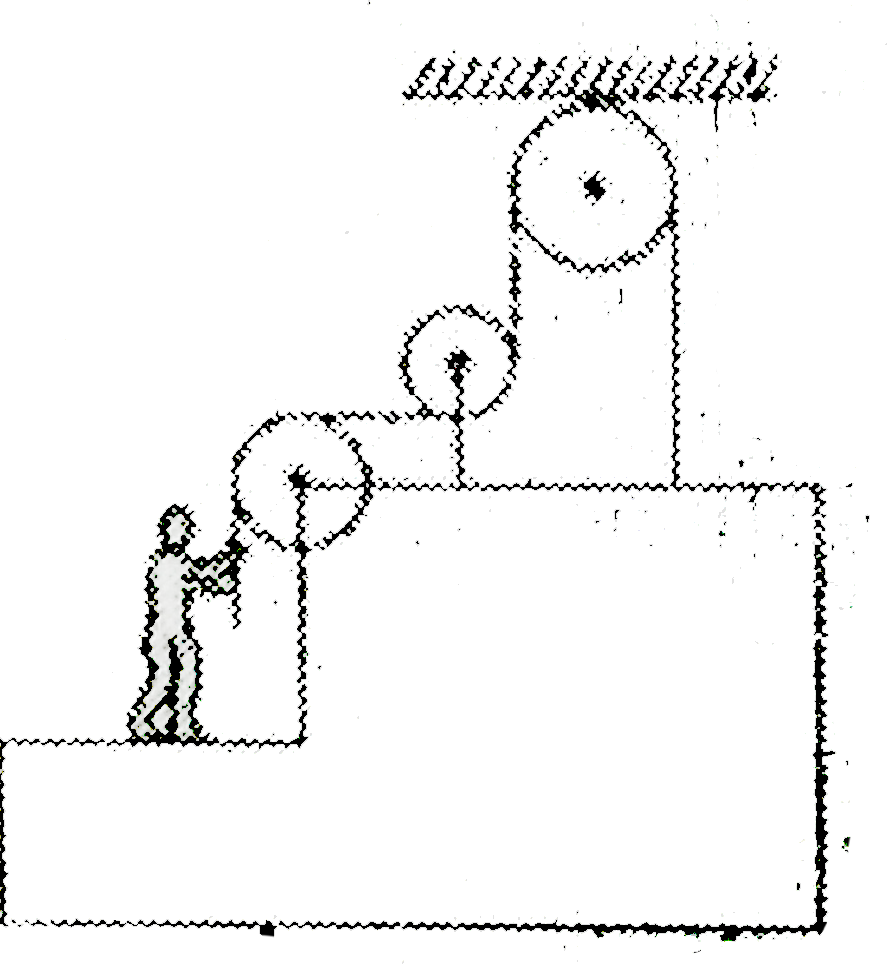 A3m/sB2m/sC1/2m/sD1m/s
A3m/sB2m/sC1/2m/sD1m/s
A man of mass 50 kg is standing on one end of a stationary wooden plank resting on a frictionless surface. The mass of the plank is 100 kg its length is 75 m and the coefficient of friction between the man the plank is 0.2 Find the least possible time (in sec) in which the man reach the other end starting from rest and stopping at the other end.
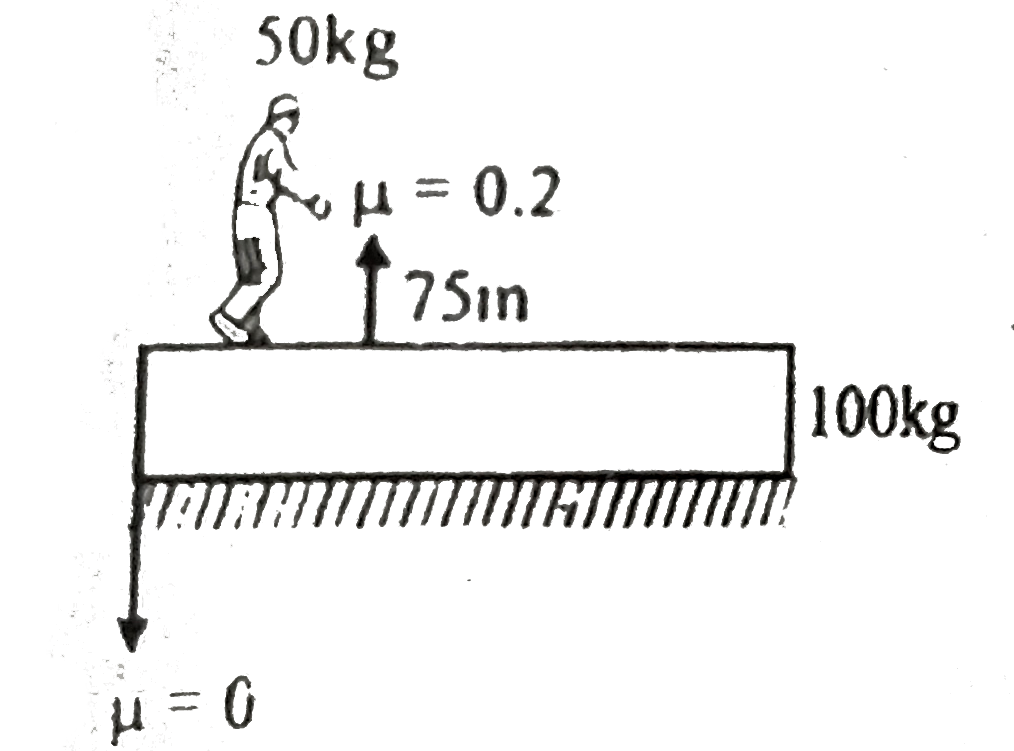
View SolutionA standing wave is set up in a string of a variable length and tension by a vibrator of variable frequency . Both ends of the string are fixed . When the vibrator has a frequency f , in a string of length L and under tension T,n antinodes are set up in the string is doubled , by what factor should the frequency be changed so that the same number of antinodes is produced? (b) If the frequency and lenght are held constant , what tension will produce n+1 antinodes ? ( c) If the frequency is tripled and the length of the string is halved , by what factor should the tension be changed so that twice as many antinodes are produced ?
View SolutionA plank of mass M and length L is at rest on a frictionless floor. At one end of it a child of mass m is standing as shown in figure-4.41. If child walks towards the other end, find the distance, which the plank moves (a) till the child reaches the centre of the plank, (b) till the child reaches the other end of the plank.
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA string of length L fixed at both ends vibrates in its fundamental mode at a frequency v and a maximum amplitude A. (a) Find the wavelength and the wave number k. (b) Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
View Solution

