A system is shown in fig. Assume that the cylinder remains in contact with the two wedge. Then the velocity of cylinder is
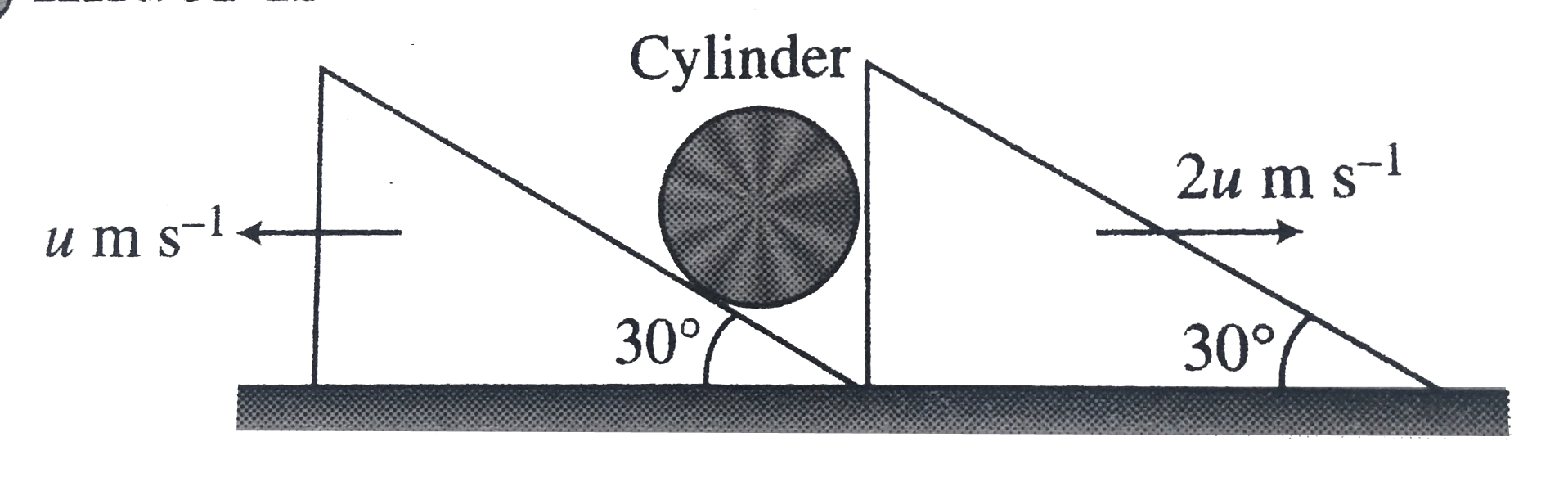
The correct Answer is:D
Method 1: Velocity components perpendicular to the contact surface remain same.
As cylinder will remain in contact with wedge A.
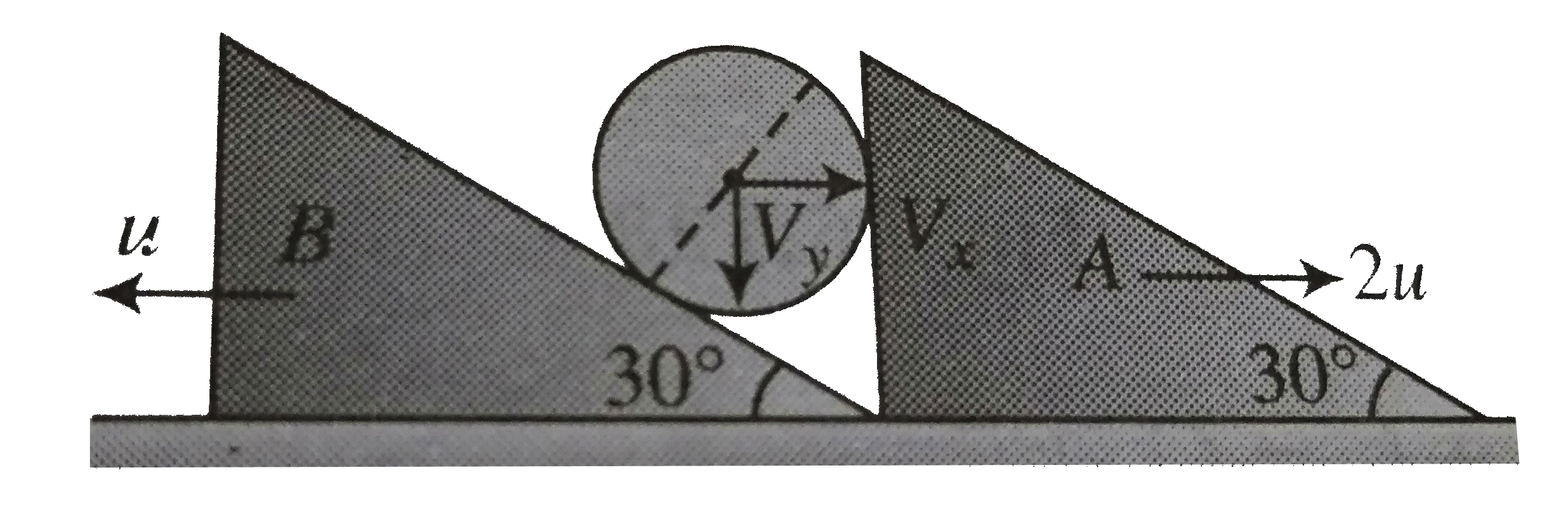
As it also remain in contact with wedge B,
.
Method 2: In the frame of A
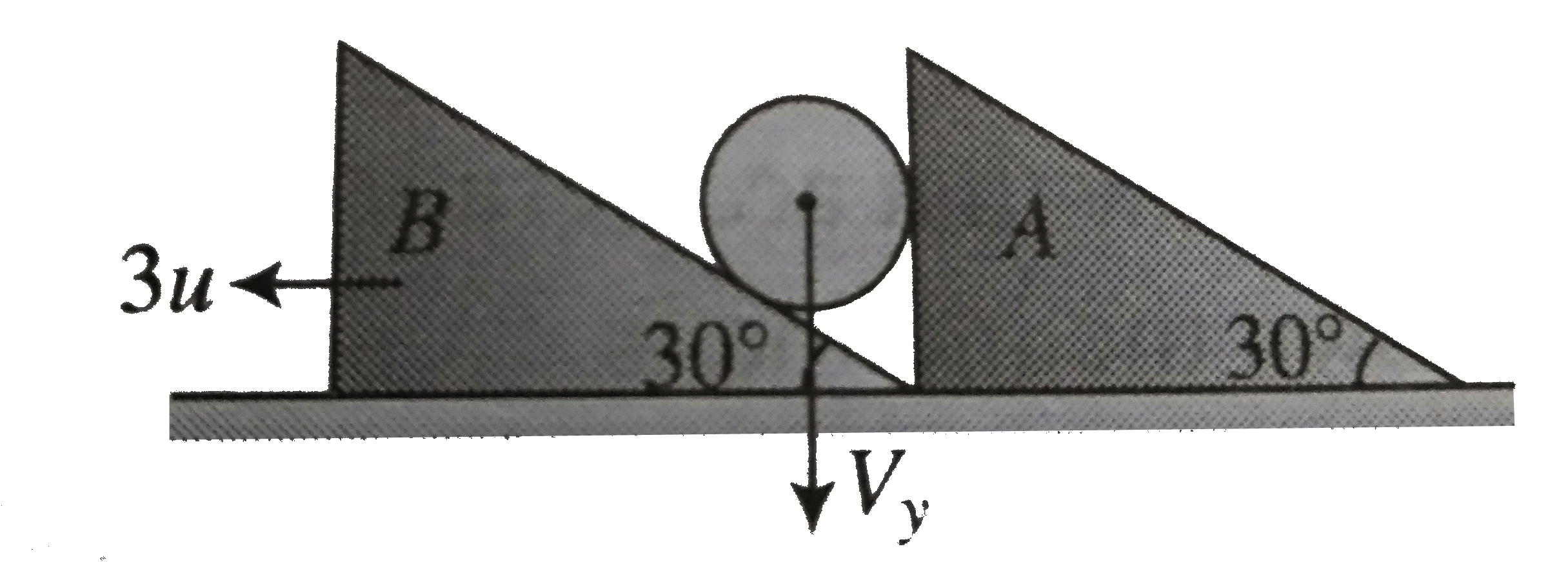
.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
System is shown in fig. and wedge is moving toward left with speed 2ms−1. Find the velocity of the block B.

View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View Solution
Knowledge Check
A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
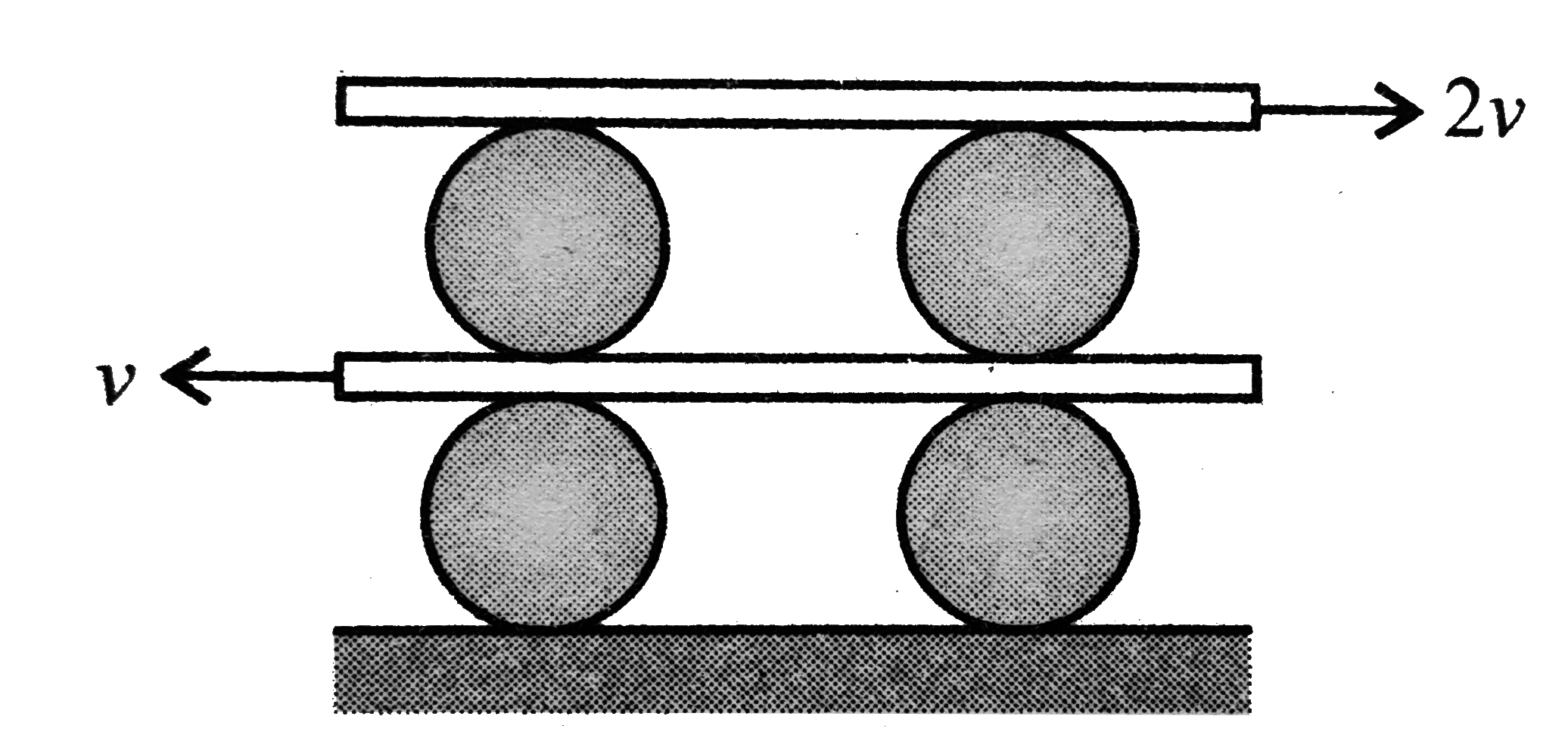 A13B3C1Dnone of the above
A13B3C1Dnone of the aboveA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
Ag2π2f2RBg4π2f2RCgπ2RD2gπ2f2RA cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
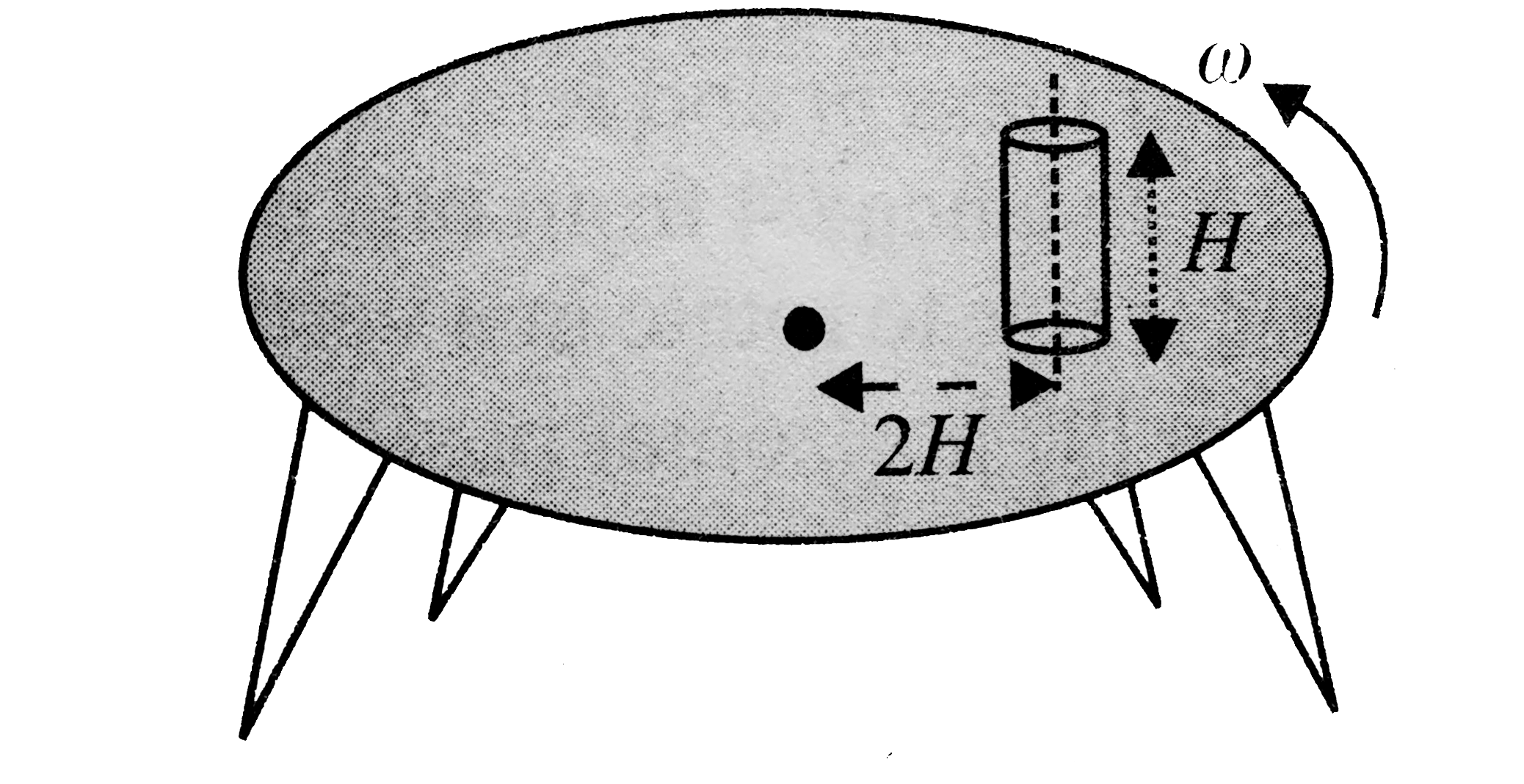 A√g2(12−H)B√g(12−H)C√g4HD√g8H
A√g2(12−H)B√g(12−H)C√g4HD√g8H
A cylinder is rotating with angular velocity ω0 and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
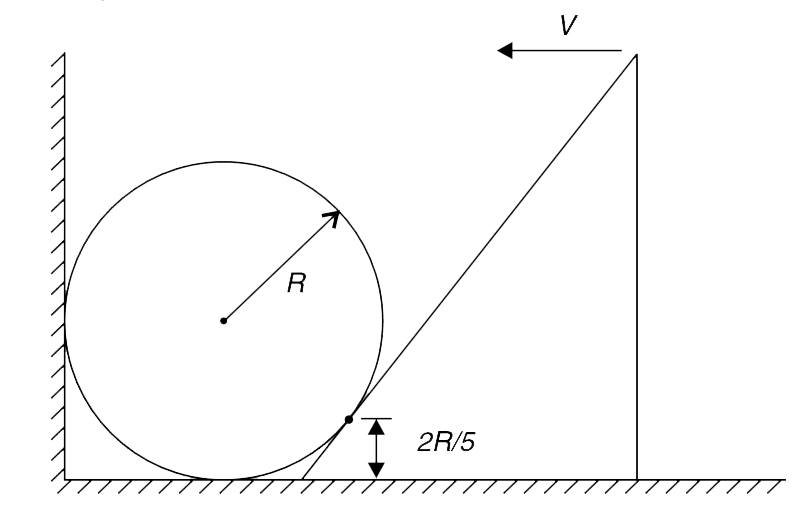
View SolutionA cylinder of radius R has been placed in a corner as shown in the fig. A wedge is pressed against the cylinder such that its inclined surfaces touches the cylinder at a height of 2R5 from thw ground. Now the wedge is pushed to the left at a constant speed V=15m/s. With what speed will the cylinder move?
View SolutionA cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.

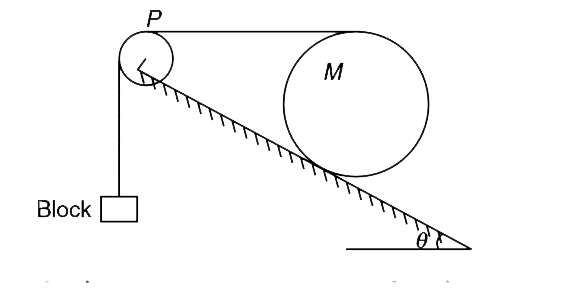
View SolutionIn the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
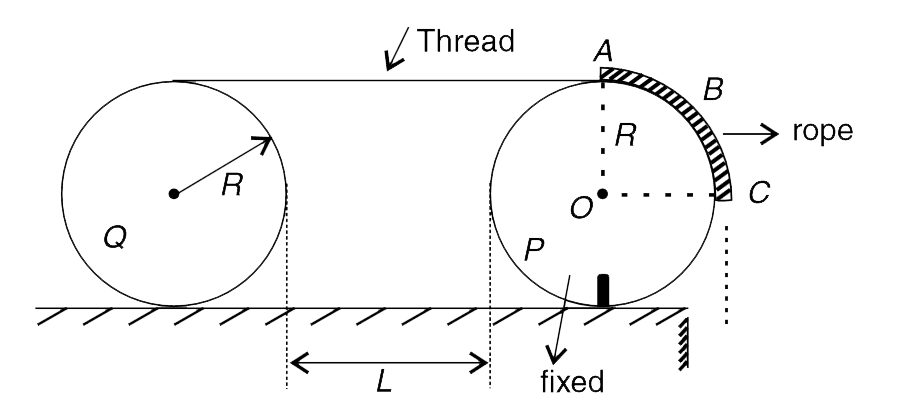
View SolutionP is a fixed smooth cylinder of radius R and Q is a disc of mass M and radius R. A light thread is tightly wound on Q and its end is connected to a rope ABC. The rope has a mass m and length πR2 and is initially placed on the cylinder with its end A at the top. The system is released from rest. The rope slides down the cylinder as the disc rolls without slipping. The initial separation between the disc and the cylinder was L=πR2 (see fig). Find the speed with which the disc will hit the cylinder. Assume that the rope either remains on the cylinder or remains vertical, it does not fly off the cylinder.
View Solution

