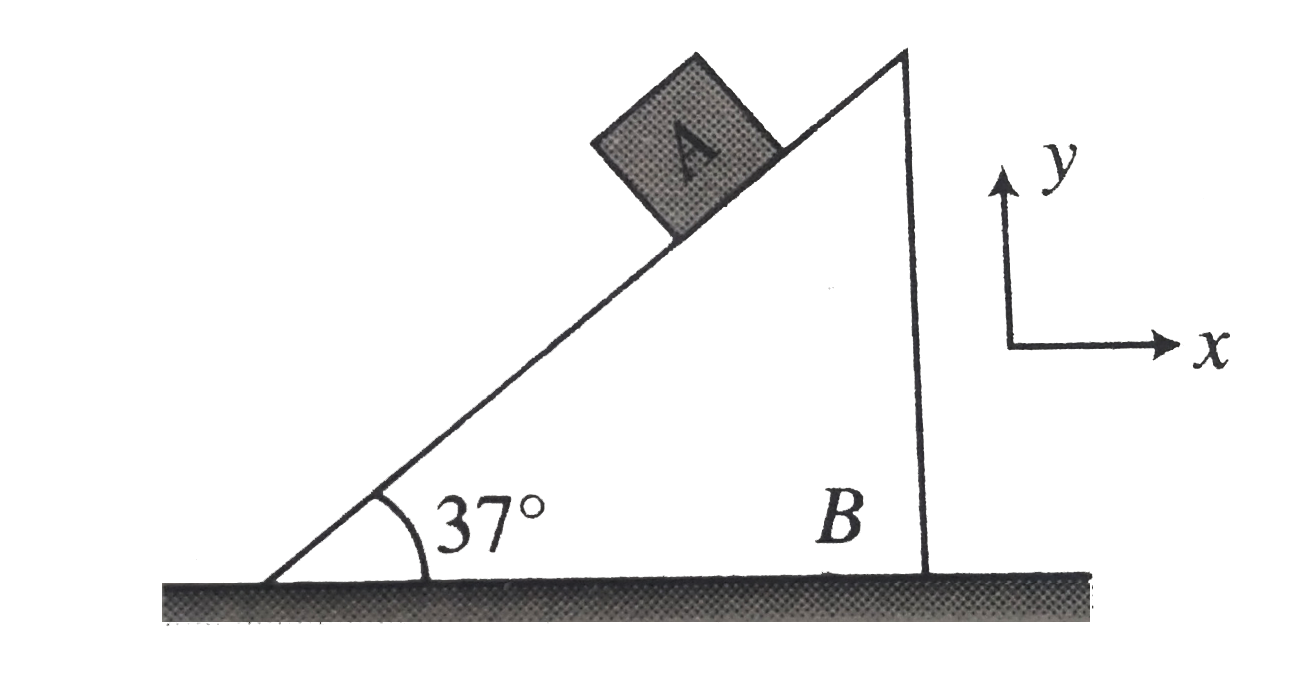
In fig, the acceleration of A is ${\to a}_{A} = 15 ˆ i + 15 ˆ j$ . Then the acceleration of B is (A remains in constact with B)

A

$6 ˆ i$

B

$- 15 ˆ i$

C

$- 10 ˆ i$

D

$- 5 ˆ i$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

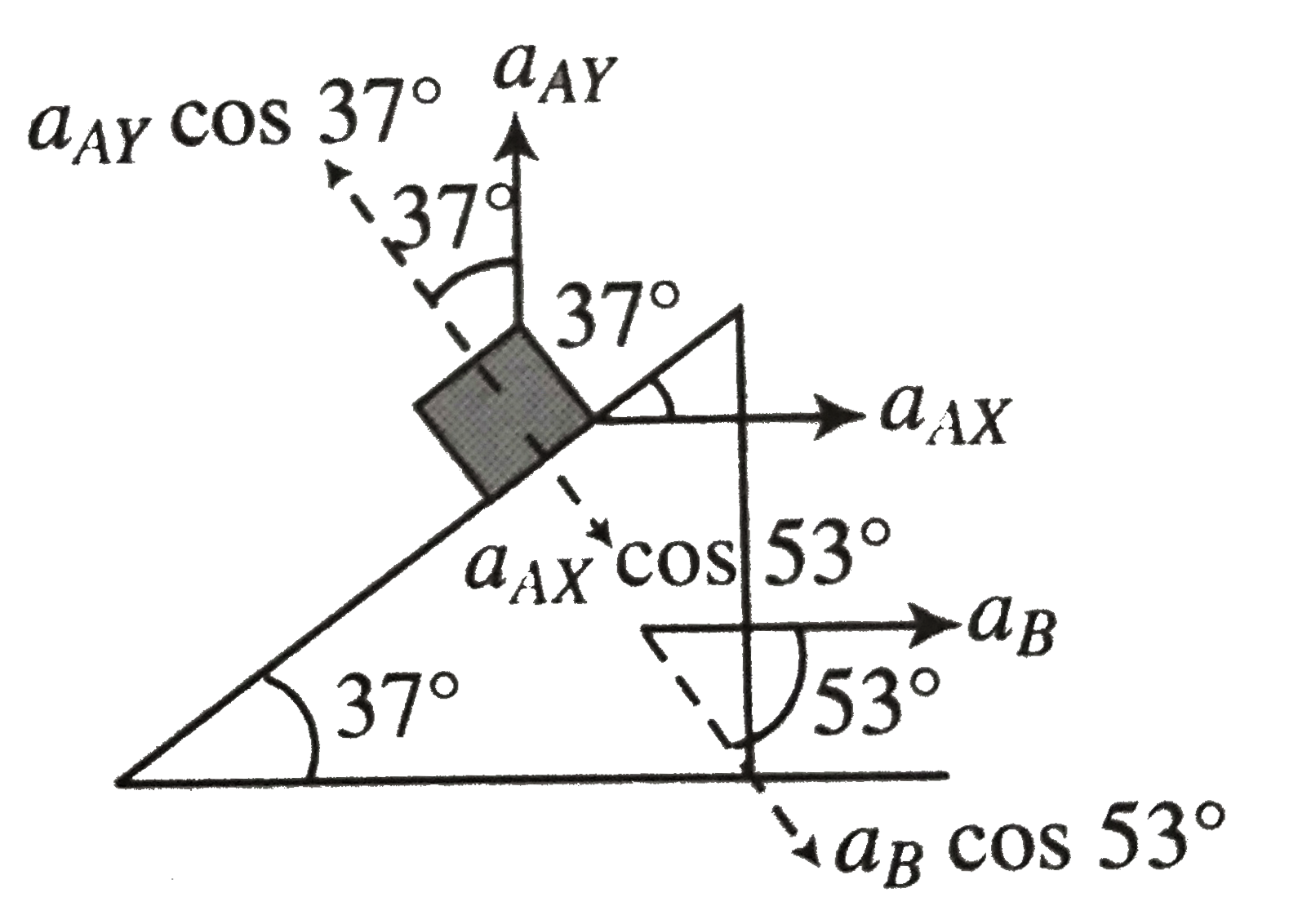
From constraint the acceleration of both block and wedge should be same in a direction perpendicular to the inclined plane as shown in fig.
${(a_{A})}_{⊥} = {(a_{B})}_{⊥}$
$a_{A X} = 15, a_{A Y} = 15$
$a_{A X} {cos 53}^{\circ} - a_{A Y} {cos 37}^{\circ} = a_{B} {cos 53}^{\circ}$
or $a_{B} = - 5 m s^{- 1} or {\to a}_{B} = - 5 ˆ i$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the figure shown the acceleration of A is, ${\to a}_{A} = 15 ˆ i + 15 ˆ j$ then the acceleration of B is (A remains in contact in B)

A $6 ˆ i$
B $- 15 ˆ i$
C $- 10 ˆ i$
D $- 5 ˆ i$
Question 2 - Select One
In the figure shown the velocity of A with respect to ground is $(20 ˆ i + 15 ˆ j) m / s$ , then what will be the magnitude of velocity of the wedge 'B' with respect to ground frame. (A remains in contact with B)

A $12 m / s$
B $25 m / s$
C $20 m / s$
Dzero
Question 3 - Select One
If $\to A = 3 ˆ i - 4 ˆ j$ and $\to B = 2 ˆ i + 16 ˆ j$ then the magnitude and direction of $\to A + \to B$ will be
A $5, {tan}^{- 1} (12 / 5)$
B $10, {tan}^{- 1} (5 / 12)$
C $13, {tan}^{- 1} (12 / 5)$
D $12, {tan}^{- 1} (5 / 12)$

CENGAGE PHYSICS-NEWTON'S LAWS OF MOTION 1-Single Correct

Home
Ask Doubt
Profile