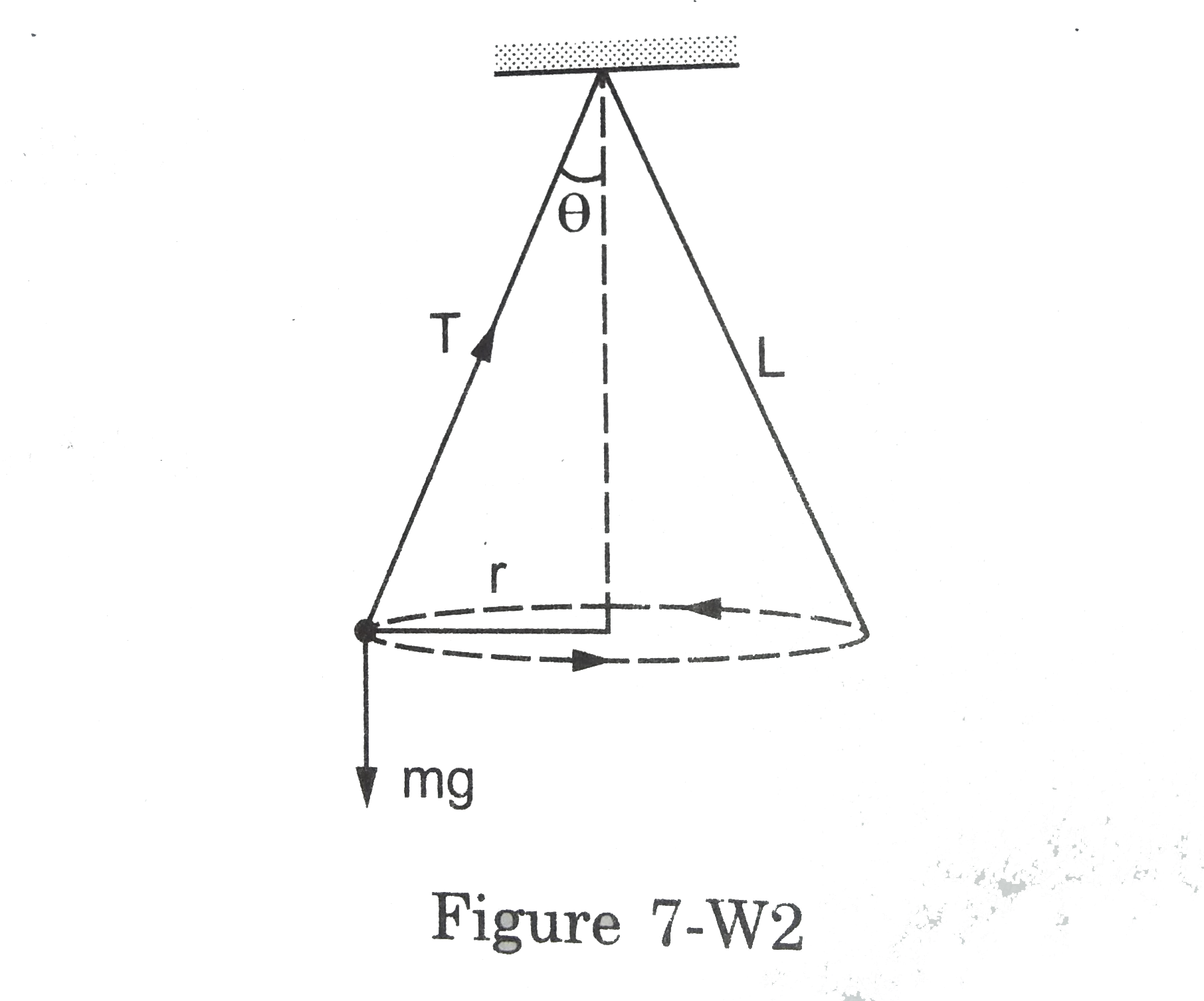
Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

The correct Answer is:(a) √g√L2−r2 (b) mgL√L2−r2
Step by step video, text & image solution for Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE(S-2)
Explore 6 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE(O-1)
Explore 22 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (S-1)
Explore 10 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Question
Explore 1 Video
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
Similar Questions
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
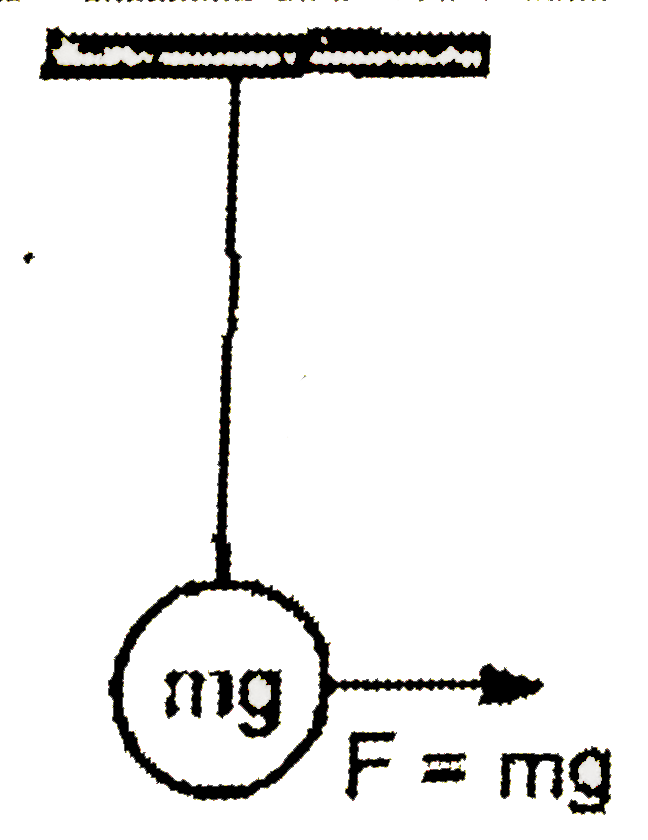
View SolutionA pendulum bob of mass m is suspended at rest. A constant horizontal force F=mg starts acting on it. Find
(a) the maximum angular defection of the string.
(b) the maximum possible tension in the string.
View Solution
Knowledge Check
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of tan−1(a/g) with the verticalBThe string makes an angle of tan−1(1−ag) with the verticalCThe tension in the string is m√a2+g2DThe tension in the string is m√g2−a2
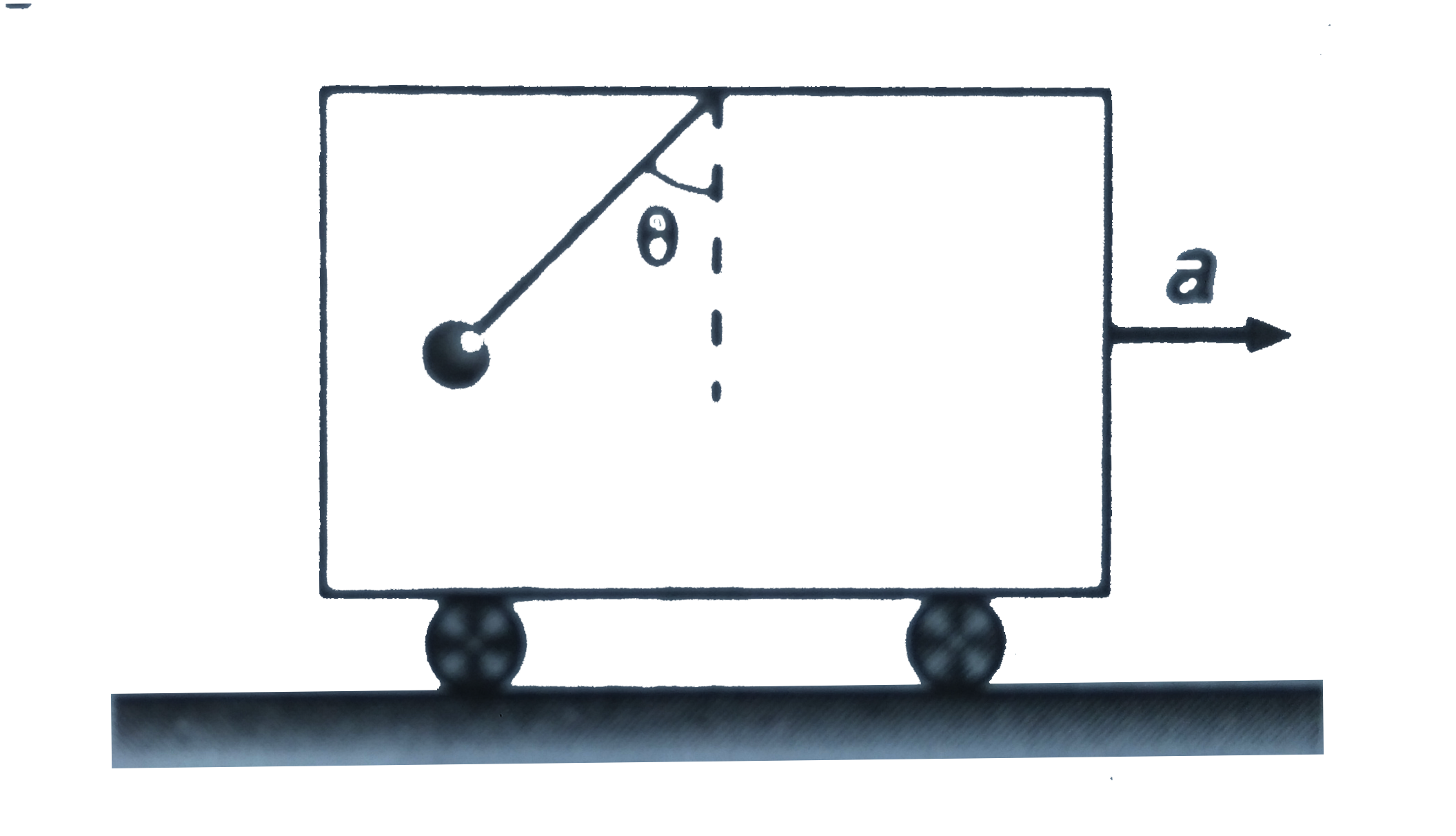
A bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
View SolutionIn a constant , when the bob moves in a horizontal circle of radius r, with uniform speed v, the string of length L describes a cone of semivertical angle θ . The tension in the string is given by
View SolutionIn a conical pendulam, when the bob moves in a horizontal circle of radius r with uniform speed v, the string of length L describes a cone of semivertical angle θ. The tension in the string is given by
View Solution

