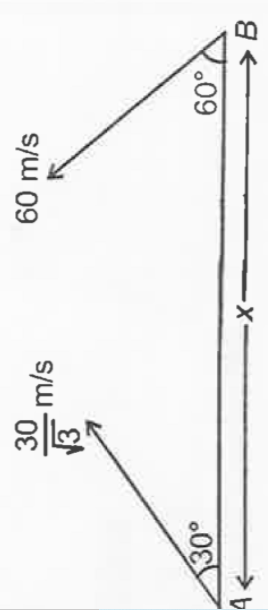
Two particles are separated at a horizontal distance as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .
.
Let are the horizontal distances travelled by particle , respectively, in time .
….(i)
and …(ii)
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.4
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Two balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
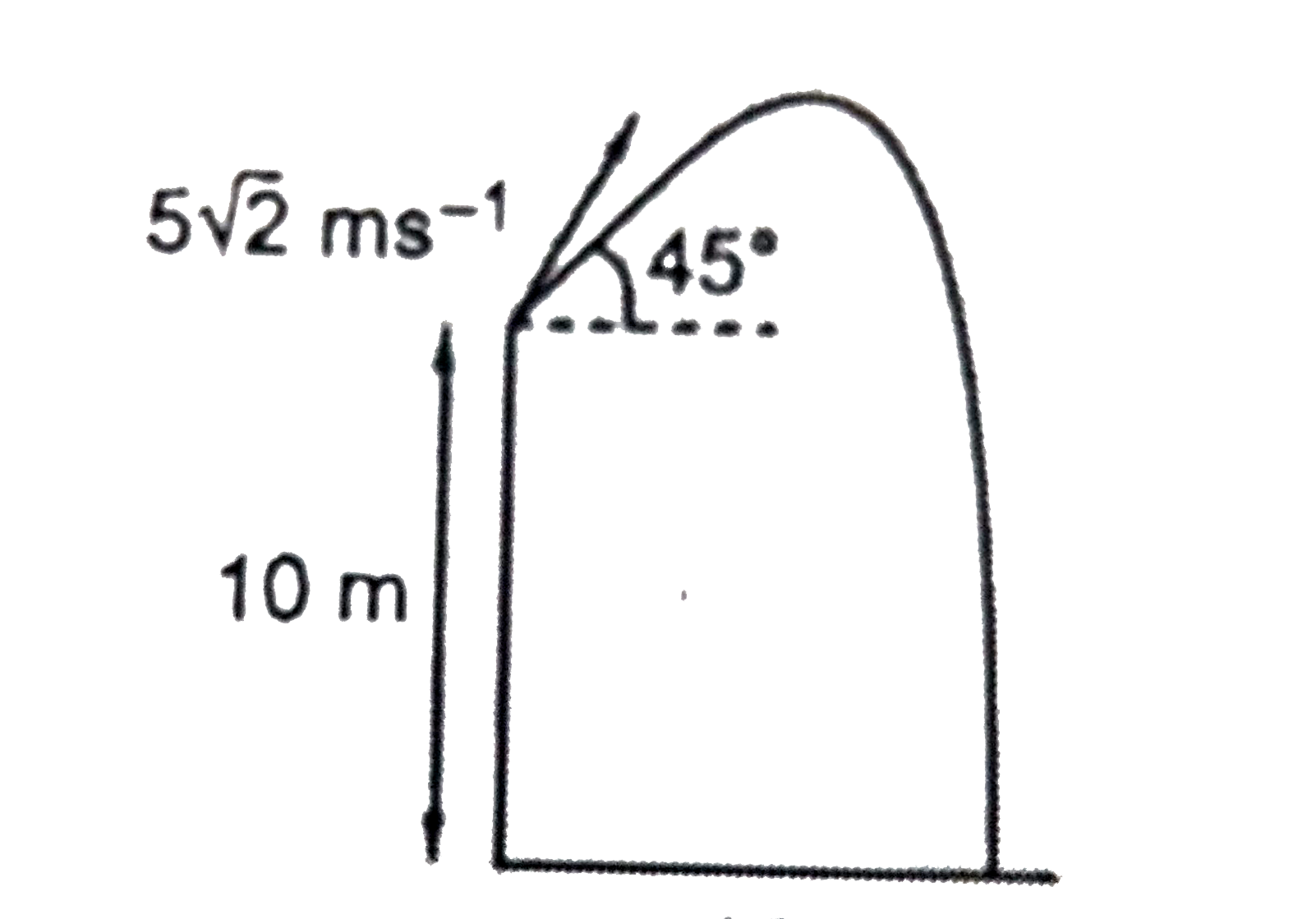
View SolutionParticle projected from tower fo heigh 10m as shown in figure. Find the time (in sec) after which particle will hit the ground.
View Solution
Knowledge Check
In the figure shown, find
(a) the time when the particle strikes the ground at P.
(b) the horizontal distance QP
(c) velocity of the particle at P.
 A6s , 120m , 40m/s , 50m/s 37∘B3s , 12m , 40m/s , 50m/s 37∘C3s , 120m , 4m/s , 50m/s 37∘D3s , 120m , 40m/s , 50m/s 37∘
A6s , 120m , 40m/s , 50m/s 37∘B3s , 12m , 40m/s , 50m/s 37∘C3s , 120m , 4m/s , 50m/s 37∘D3s , 120m , 40m/s , 50m/s 37∘Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
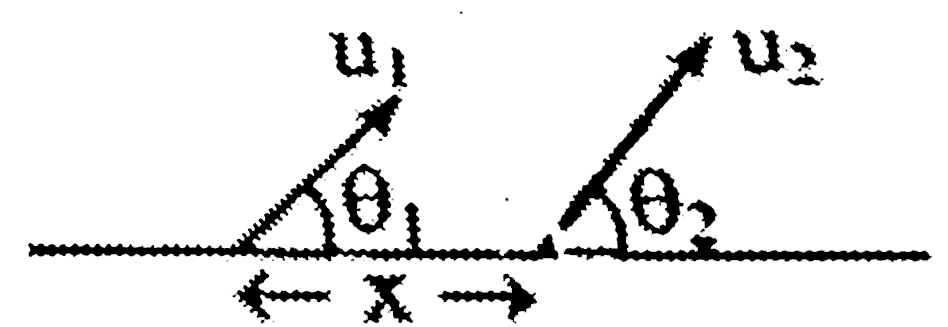 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two particles are projected simultaneously from two points, O and O' such that d is the horizontal distance and h is the vertical distance between them. They are project at the saem inclination α to the horizontal with the same speed v as shown. The time after which their separation becomes minimum is
 Ad/(vcosα)B2d/(vcosα)Cd/(2vcosα)Dd/v
Ad/(vcosα)B2d/(vcosα)Cd/(2vcosα)Dd/v
A particle moves along a horizontal line and its velocity changes with time as shown in the figure.

Calculate (i)initial acceleration, (ii)total distance described . Plot the x-t graph of the motion.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
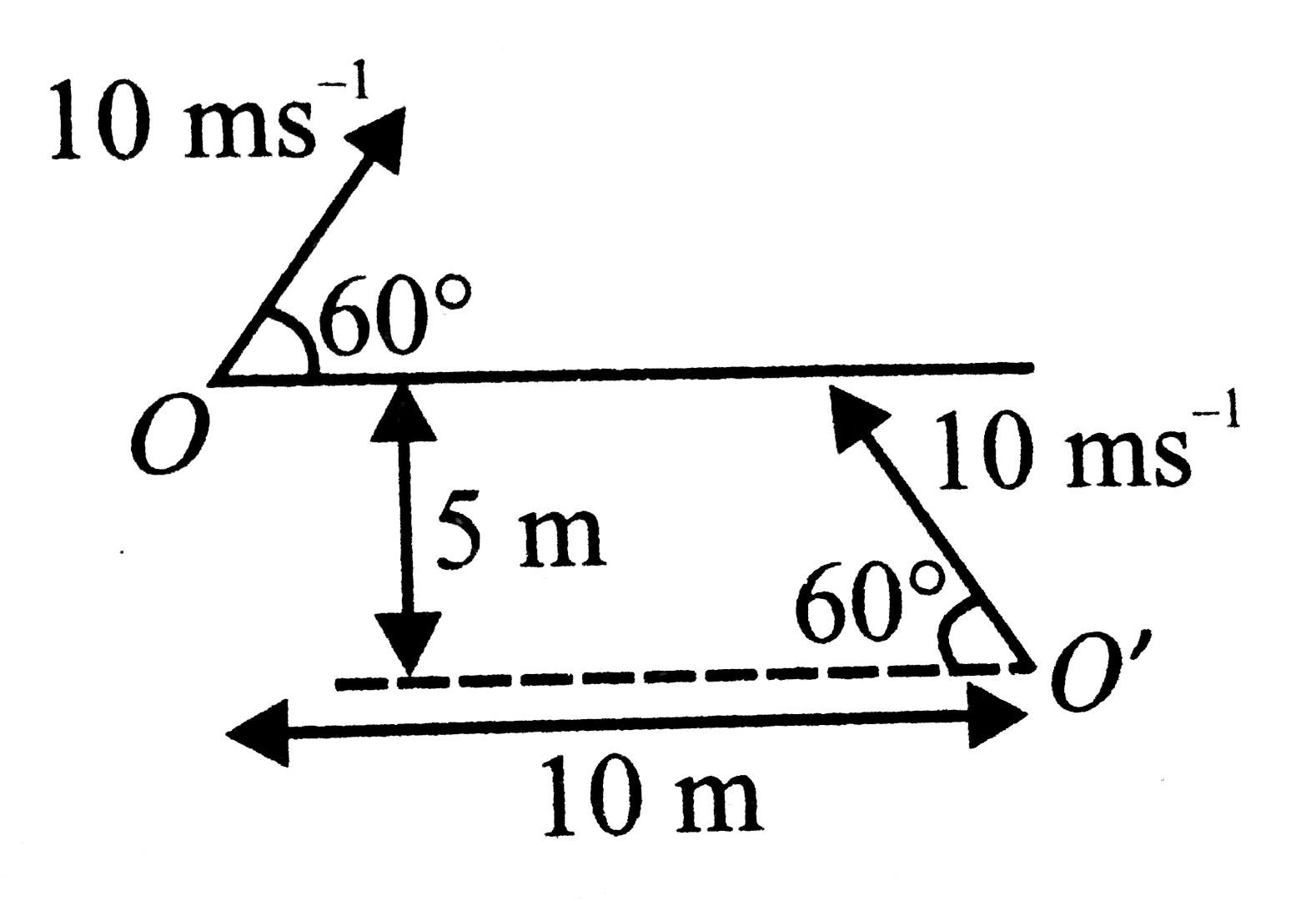
View SolutionTwo particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same meabn position , initial they are at their position exterm position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the seopration between the particle becomes 6cm
View SolutionA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
View Solution

