Two particles are projected simultaneously from two points, O and O' such that d is the horizontal distance and h is the vertical distance between them. They are project at the saem inclination α to the horizontal with the same speed v as shown. The time after which their separation becomes minimum is
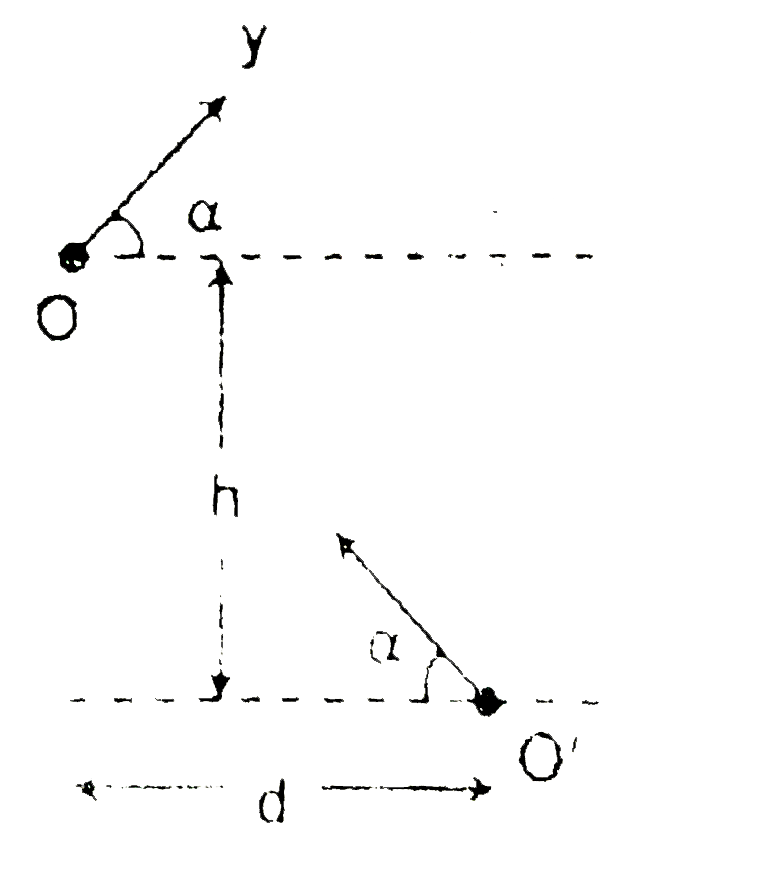
d/(vcosα)
2d/(vcosα)
d/(2vcosα)
d/v
The correct Answer is:C
As the vertical component of velocity of both the particles is same.
⇒→vy∅O=O
So the distance h between h between them will be constant with time and →vX∅O=2vcosα
Total distance between the particles is minimum when horizontal distance between them is zero
⇒t=d2vcosθ
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
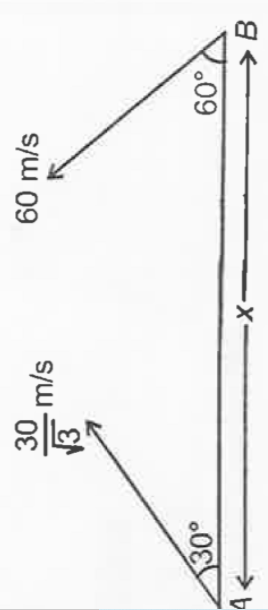
Two balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
View SolutionTwo particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .
.
View Solution
Knowledge Check
Two particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
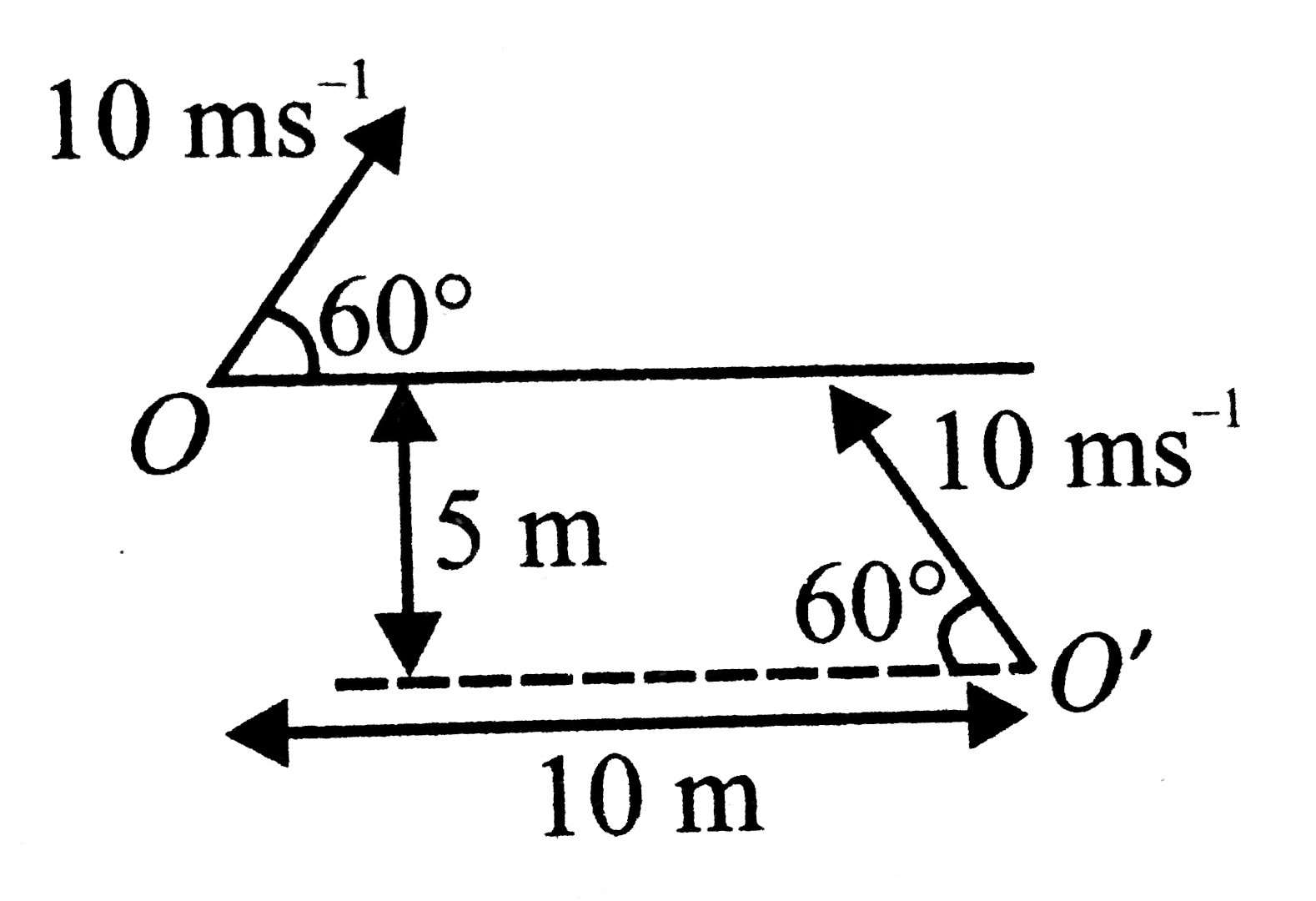 A2.5sB1sC5sD10s
A2.5sB1sC5sD10sTwo particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
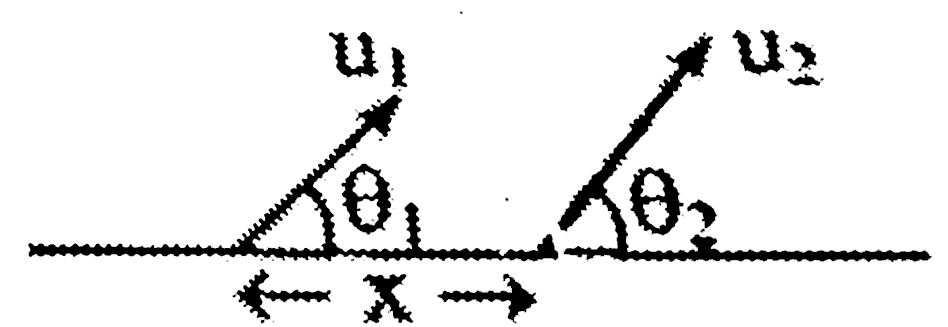 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
Two particles are projected from two high rise buildings simultaneously as shown then find minimum distance between particles.

View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
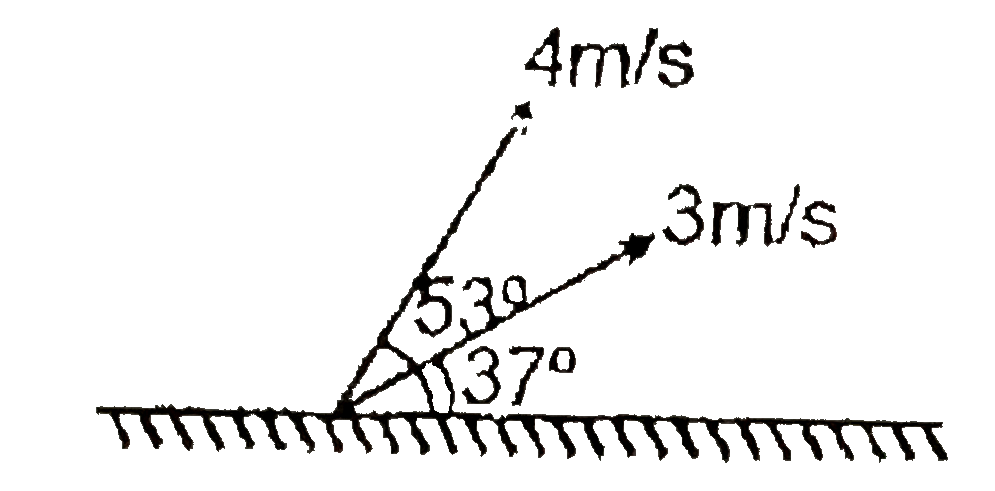
View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionTwo particles A and B projected simultaneously from a point situated on a horizontal place. The particle A is projected vertically up with a velcity vA while the particle B is projected up at an angle 30∘ with horizontal with velocity vB. After 5s the particles were observed moving mutually perpendicular to each other. The velocity of projection of the particle vAandvB respectively are:
View Solution
