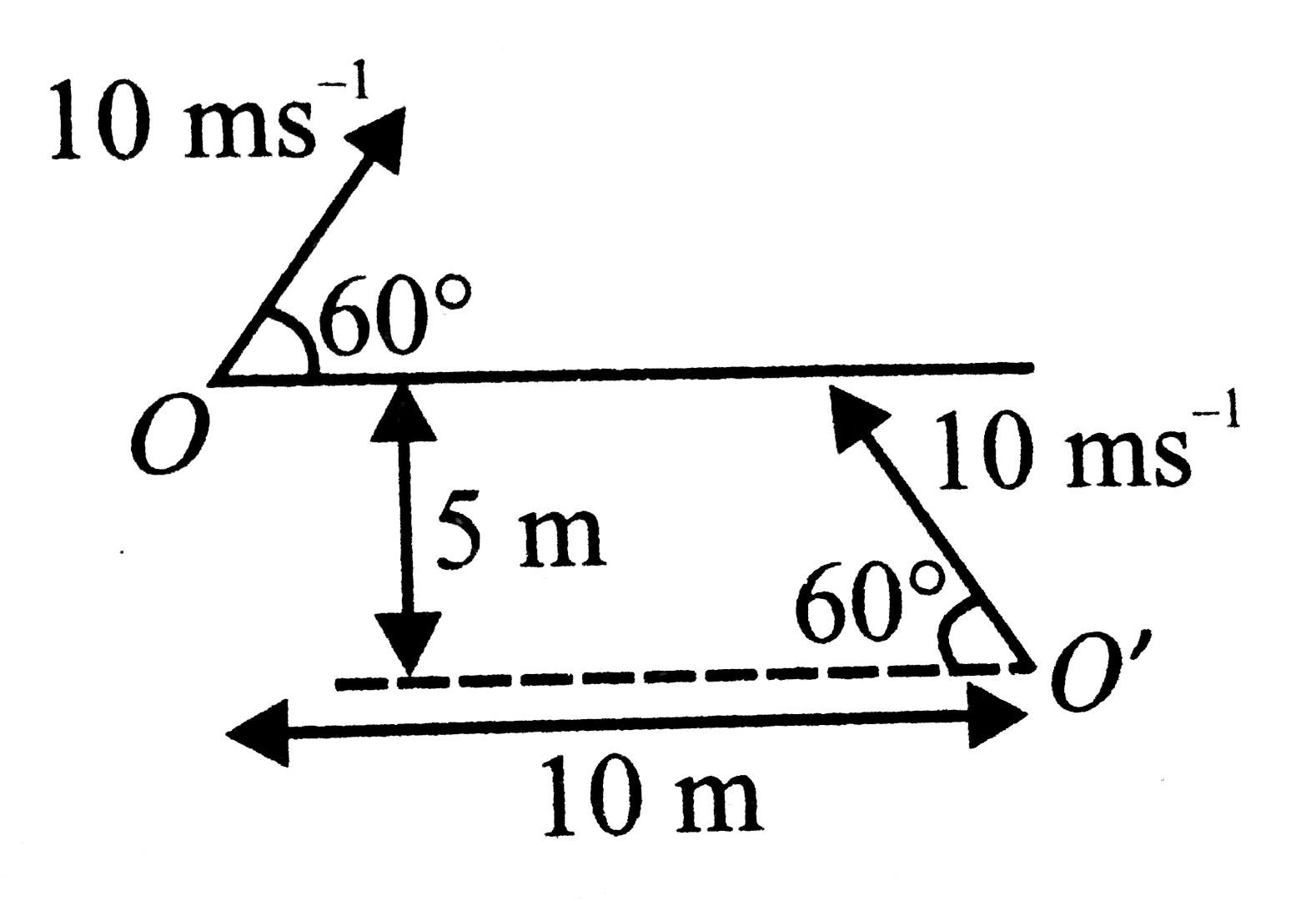
Two particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
2.5s
1s
5s
10s
The correct Answer is:B
Let us find the relative velocity of O. w.r.t O'.
→v∅O'=→vO−→vO'=(10cos60∘ˆi+10sin60∘ˆj)
−[10cos60∘(−ˆi)+10sin60∘ˆj]=10ˆi
This is along the horizontal direction.

If we assume O' to be at rest, then O will move along OA w.r.t O' and the minimum separation will be when particle O is at A.
For this the relative displacement travelled =OA=10m
Time taken =10VO/O'=1010=1s
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Two bodies are projected at angle of 45∘ and 60∘ with the horizontal with same velocity simultaneously. Ratio of their horizontal range is.
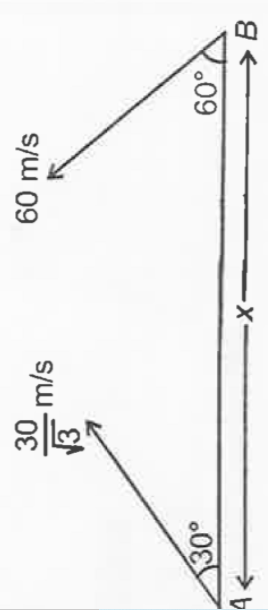
View SolutionTwo balls are projected from two points A and B,x metre apart as shown in figure.The time after which the horizontal distance between them become zero is
View Solution
Knowledge Check
Two particles are projected simultaneously from two points, O and O' such that d is the horizontal distance and h is the vertical distance between them. They are project at the saem inclination α to the horizontal with the same speed v as shown. The time after which their separation becomes minimum is
 Ad/(vcosα)B2d/(vcosα)Cd/(2vcosα)Dd/v
Ad/(vcosα)B2d/(vcosα)Cd/(2vcosα)Dd/vTwo particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
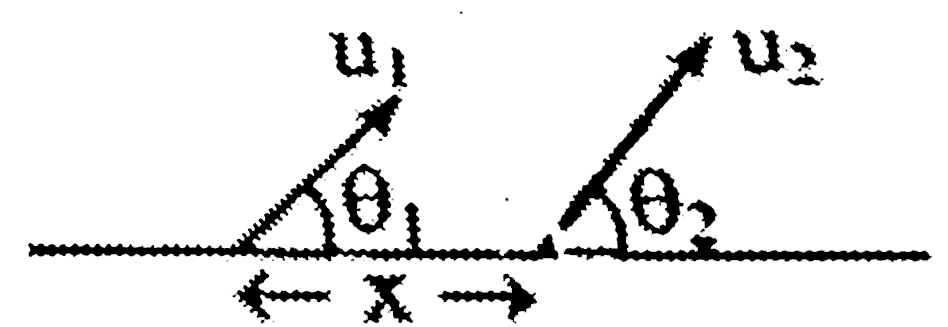 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
Two particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .
.
View SolutionTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
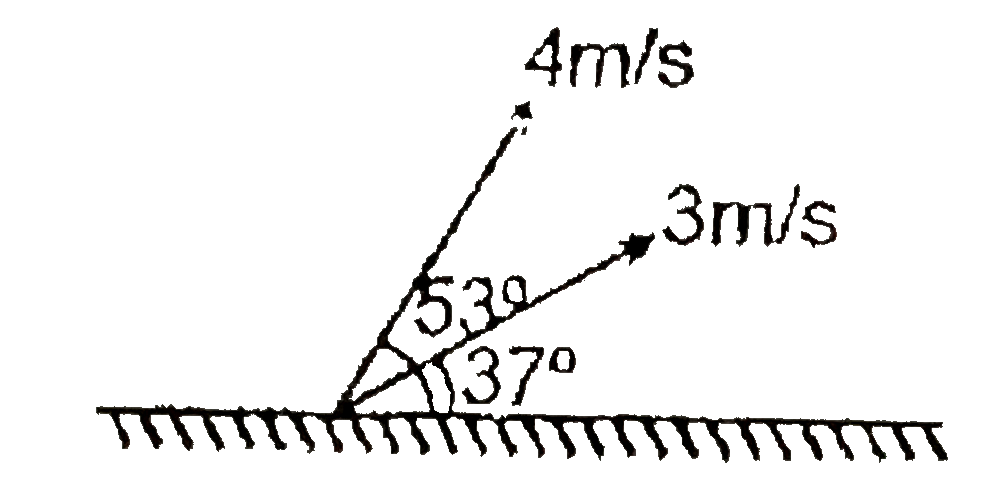
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
View Solution
