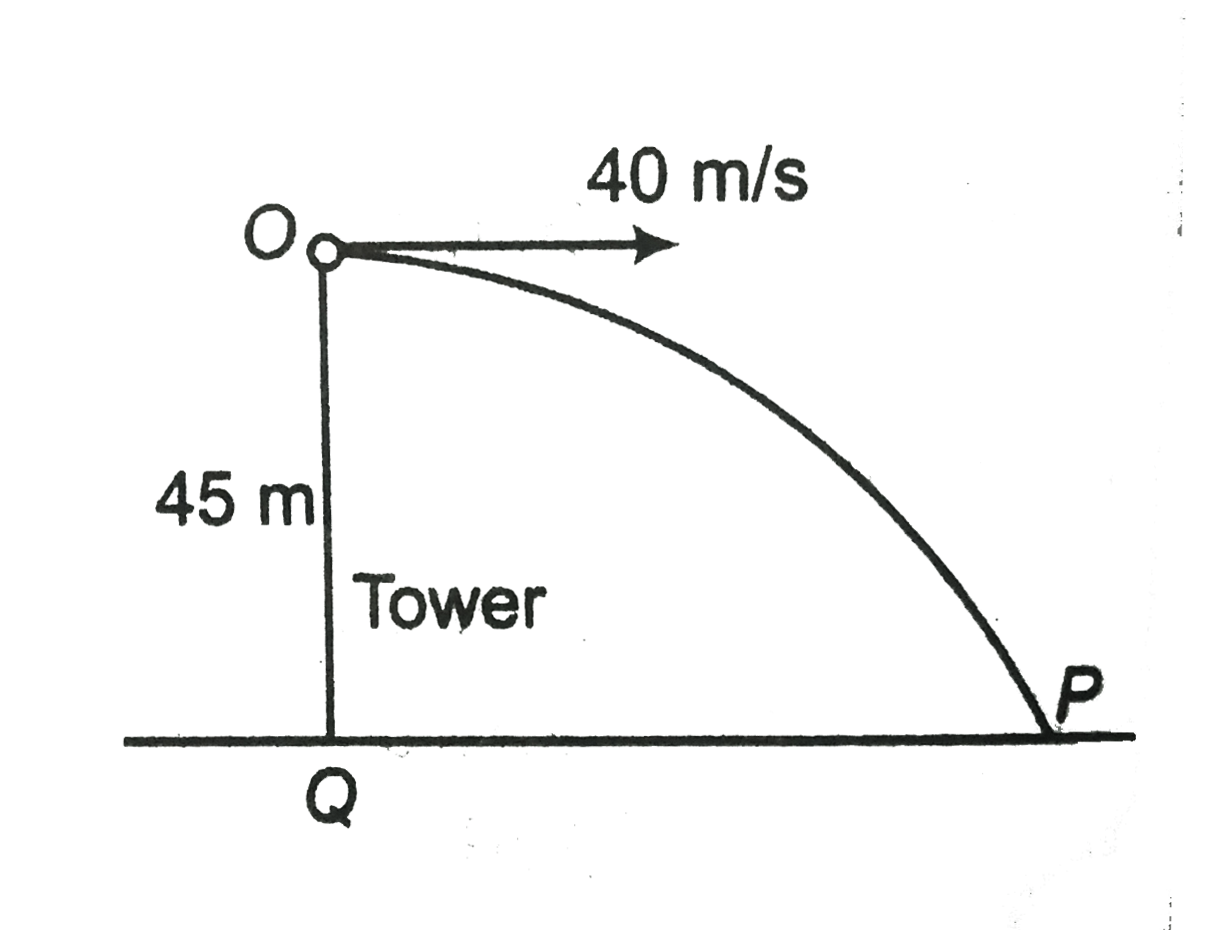
In the figure shown, find
(a) the time when the particle strikes the ground at P.
(b) the horizontal distance QP
(c) velocity of the particle at P.
6s , 120m , 40m/s , 50m/s 37∘
3s , 12m , 40m/s , 50m/s 37∘
3s , 120m , 4m/s , 50m/s 37∘
3s , 120m , 40m/s , 50m/s 37∘
The correct Answer is:D
(a)t=√2hg=√2×4510=3s
(b) Horizontal distance QP=40t
=40×3=120m
(c) Horizontal component of velocity at P = 40m/s
Vertical compound of velocity =gt=10t=10×3=30m/s

Net velocity v =√(40)2+(30)2=50m/s
tanθ=3040or34
∴θ=tan−1(34)=37∘ .
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 41videos
PROJECTILE MOTION
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 53videos
PROJECTILE MOTION
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 21videos
PROJECTILE MOTION
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
Similar Questions
In the figures shown, three particles are thrown from a tower of height 40 m as shown in figure. In each case find the time when the particles strike the ground and the distance of this point from foot of the tower.
 ,
,  ,
,  .View Solution
.View SolutionTwo particles A and B are moving along x-axis. Their x-coordinate versus time graphs are as shown below

(a) Find the time when the particles start their journey and the x-coordinate at that time.
(b) Find velocities of the two particles.
(c) When and where the particles strike with each other.View SolutionA particle is projected from a tower of height 25 m with velocity 20√2m/s at 45∘. Find the time when particle strikes with ground. The horizontal distance from the foot of tower where it strikes. Also find the velocity at the time of collision.
View SolutionA particle is parojected vertically upwards from grund with initial velocity u.
a. Find the maximum height H the particle will attain and time T that it will attain and time T that it will take to return to the ground .
 .
.
b. What is the velocity when the particle returns to the ground?
c. What is the displacement and distance travelled by the particle during this time of whole motion.View SolutionA ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA particle is released from a certain height H=400m. Due to the wind, the particle gathers the horizontal velocity component vx=aywhere a =(√5)s−1 and y is the vertical displacement of the particle from the point of release, then find
(a) the horizontal drift of the particle when it strikes the ground ,
(b) the speed with which particle strikes the ground.View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?View SolutionA particle is projected horizontally as shown from the rim of a large hemispherical bowl. The displacement of the particle when it strikes the bowl the first time is R. Find the velocity of the particle at that instant and the time taken.
 View Solution
View SolutionTwo particles are separated at a horizontal distance x as shown in (Fig. 5.57). They are projected at the same time as shown in the figure with different initial speed. Find the time after which the horizontal distance between the particles becomes zero.
 .View Solution
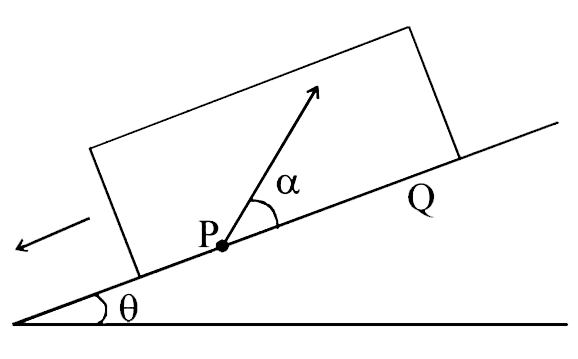
.View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
 View Solution
View Solution

