A particle is projected horizontally as shown from the rim of a large hemispherical bowl. The displacement of the particle when it strikes the bowl the first time is R. Find the velocity of the particle at that instant and the time taken.

Video Solution
Text Solution
The correct Answer is:uˆi+√√3Rgˆj,√√3Rg
∴ Vertical displacement of particle=R√32
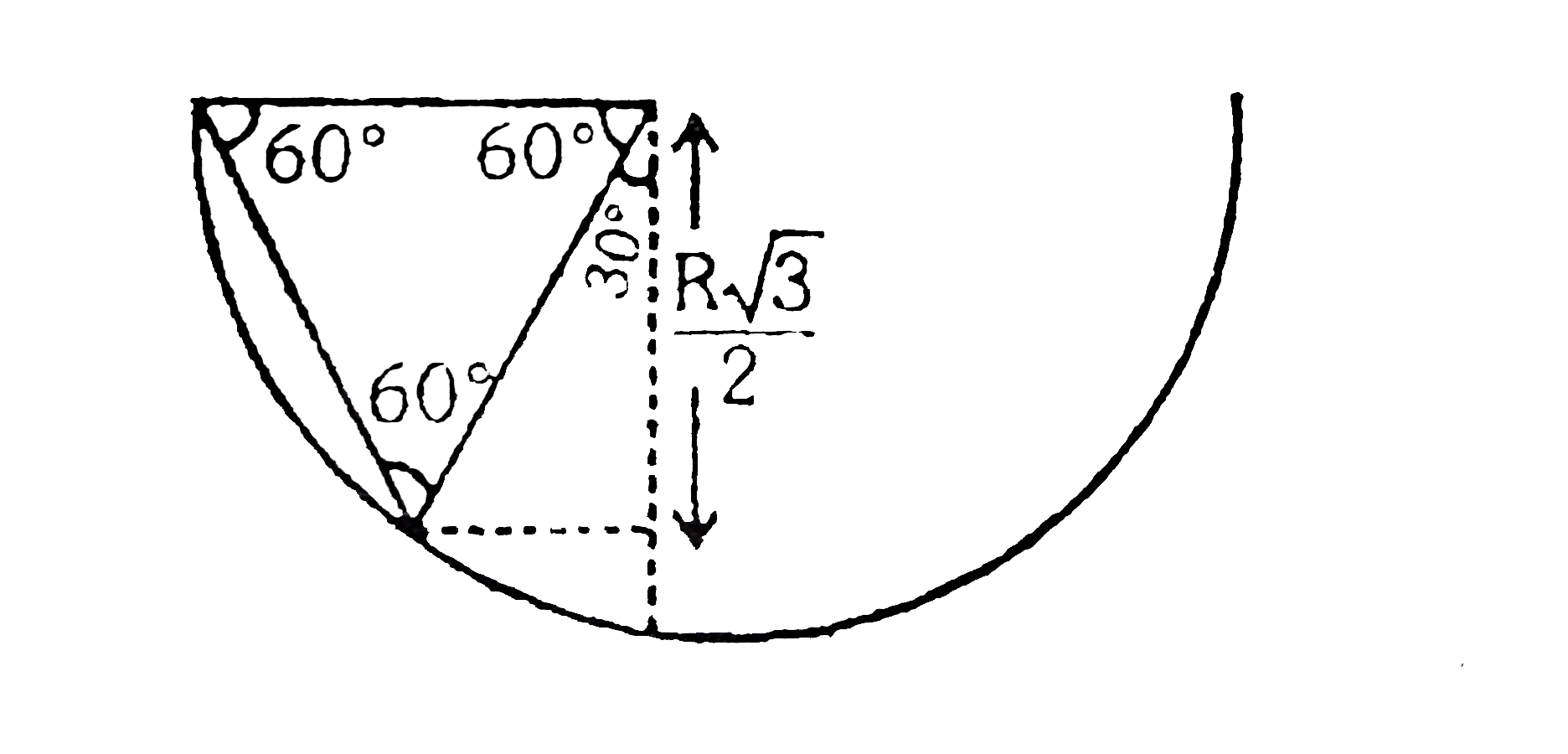
Time for this =
⎷2×R√32g=√√3Rg
→v(t)=uˆi+gtˆj=uˆi+g×√√3Rgˆj=uˆi+√√3Rgˆj
|
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Exercise-04[B]
Explore 14 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Exercise-05 [A]
Explore 11 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Comprehension#7
Explore 3 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
Knowledge Check
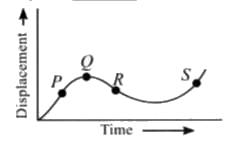
The displacement-time graph of moving particle is shown below

The instantaneous velocity of the particle in negative at the pointADBFCCDEThe displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
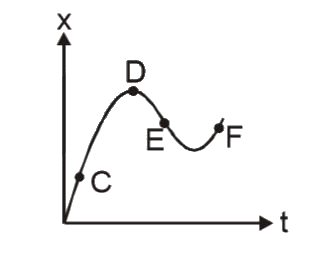
ACBDCEDFThe displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
 ACBDCEDF
ACBDCEDF
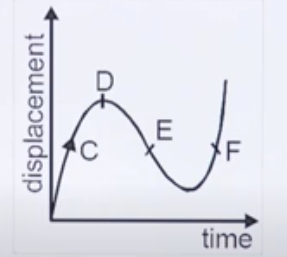
The displacement time graph of a moving particle is shown below
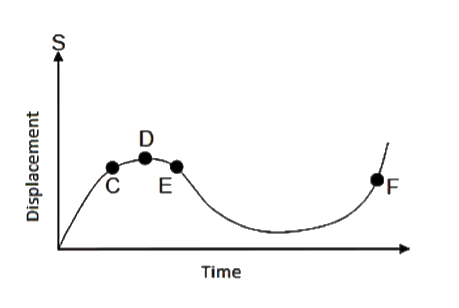
The instantaneous velocity of the particle is negative at the point
View SolutionThe displacement-time graph for two particles is as shown. Find the ratio of their velocities.
View SolutionThe displacement of a particle as a function of time is shown in . It indicates
 .
.
View SolutionThe displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
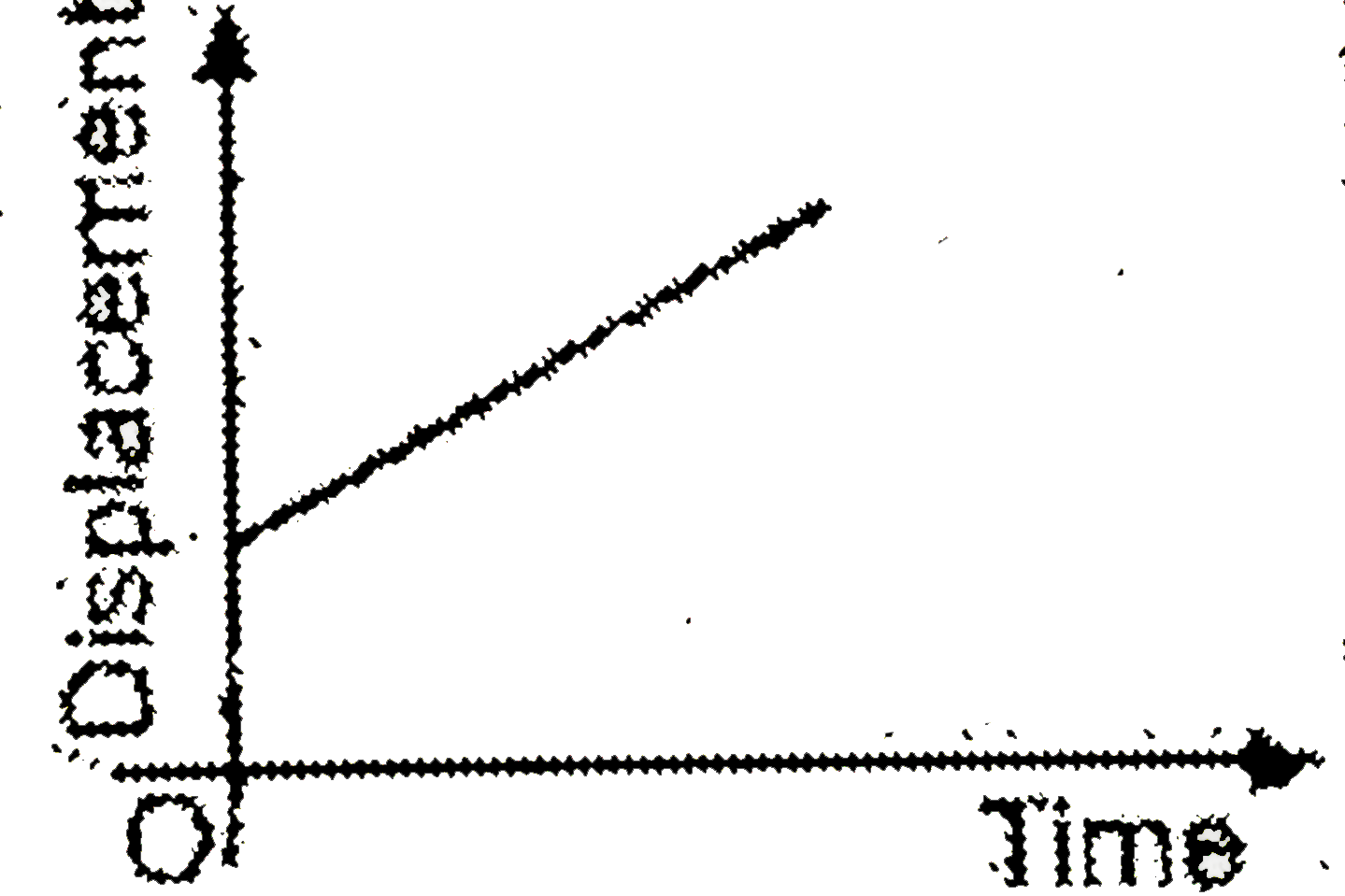
View SolutionIf the time-displacement graph of a particle is parallel to the-axis, the velocity of the particle is
View Solution