Find the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
The correct Answer is:zero
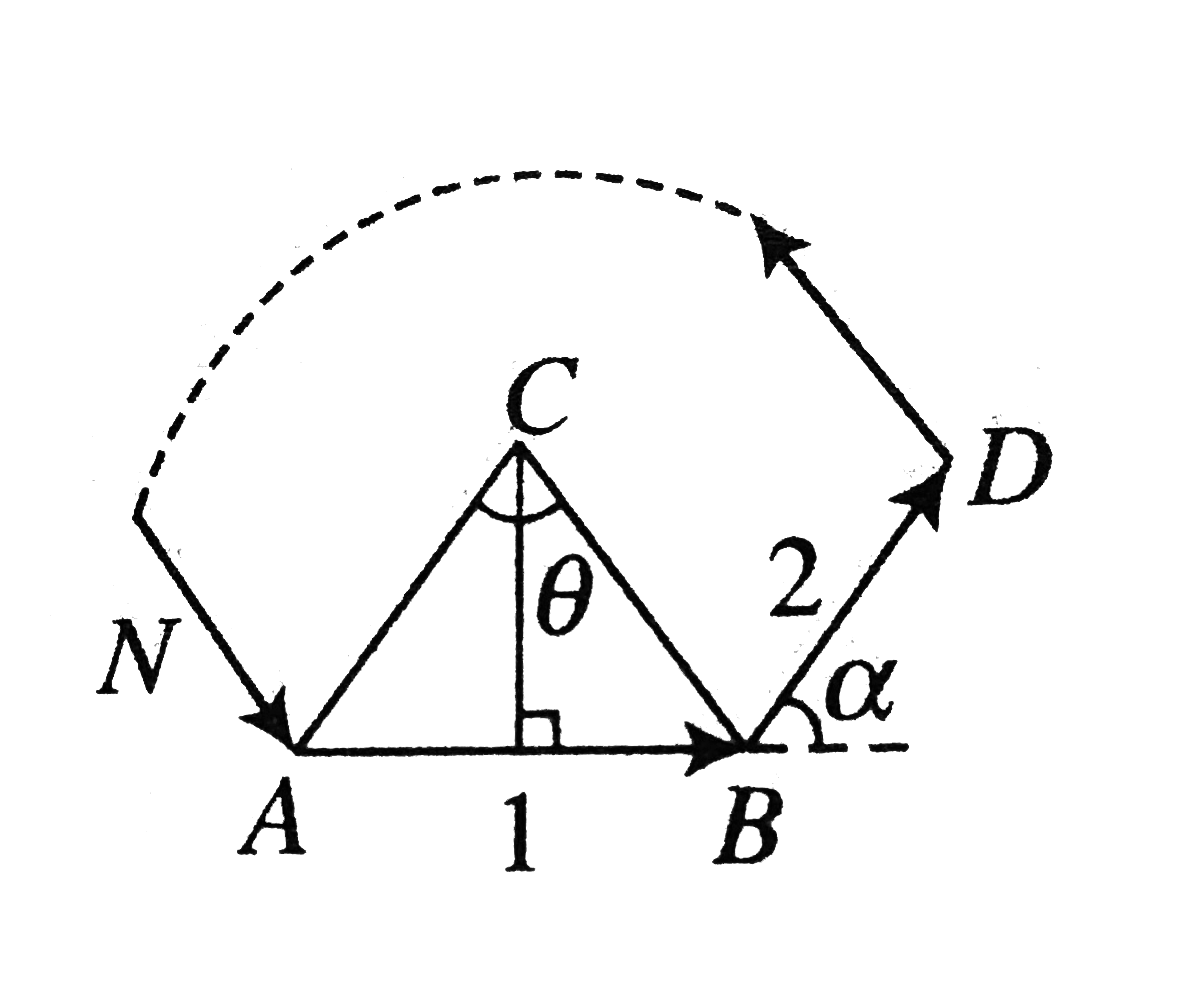
consider a regular polygon of N sides. Each side of the poygon is same. C is the centre of polygon (figure) θ=2π/N→θ is the angle subtended at the centre of polygon by any one side.
We can prove that α=θ as
∠ABC+∠CBD+α=180∘..(i)
But ∠ABC=∠CBD=90∘−θ2..(ii)
From Eqs.(i) and (ii), we get α=θ
⇒α=2πN
So if we have N vector of equal magnitude and they are arranged in such a way that each vector makes an angle 2π/N(=α) with its preceding vector, we find that the head of the last vector will coincide with the tail of the first vector. Hence, the resultant of all these vector becomes zero.
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Single Correct
Explore 51 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
Find the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
View SolutionWe have n coplanar forces, each of magnitude T. If each force makes an angle 2πn with the preceding force, then the vector sum of the n forces is a null vector.
View Solution
Knowledge Check
100 coplanar forces each equal to 10 n act on a body. Each force makes angle π/50 with the preceding force. What is the resultant of the forces.
A1000 NB500 NC250 NDZero100 coplanar forces each equal to 10 N act on a body. Each force makes angle π50 with the preceding force. What is the resultant of the forces
A1000NB500NC250NDzeroTwo forces each of magnitude 2N, act at an angle of 60∘. What is the magnitude of the resultant force ?
A√2NB√6NC√8ND√12N
If the resultant of two forces each of magnitude F is 2F, then the angle between them will be?
View SolutionVector sum of two forces of 10N and 6N cannot be:
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionThe greatest & the least magnitude of the resultant of two forces of constant magnitudes are P & Q respectively. If the forces act at an angle 2α, then prove that the magnitude of their resultant is given by √P2cos2α+Q2sin2α.
View SolutionThree are N coplancar vectors each of magnitude V Each vector is inclined to the preceding vector atangle 2πN What is the magnitude of their resultant ?
View Solution

