Forces X,Y and Z have magnitudes 10N5(√3−1)N and 5(√3+1)N, respectively. The forces Y and Z act in the same direction as shown in (figure) The resultant of X and Y and the resultant of X and Z have the same magnitudes. Find θ, the angle between X and Y.

The correct Answer is:150∘
Resultant of →X+→Y=→X+→Z
(10)2+(5√3−1)2)+2.10.(5√3−1)cosθ
=(10)2+(5√3+1)2+2.10.(5√3+1)cosθ
or (5√3−1)2−(5√3+1)2=2.10cosθ[(5√3+1)−(5√3−1)]
(2.5.√3)(−2)−2.10cosθ[2]=−510√3=cosθ
−√32=cosθ⇒θ=150∘
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Single Correct
51 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Two forces acting in opposite direction have resultant 10N and when acting perpendicularly have resultant 50N. Find the magnitude of forces.
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
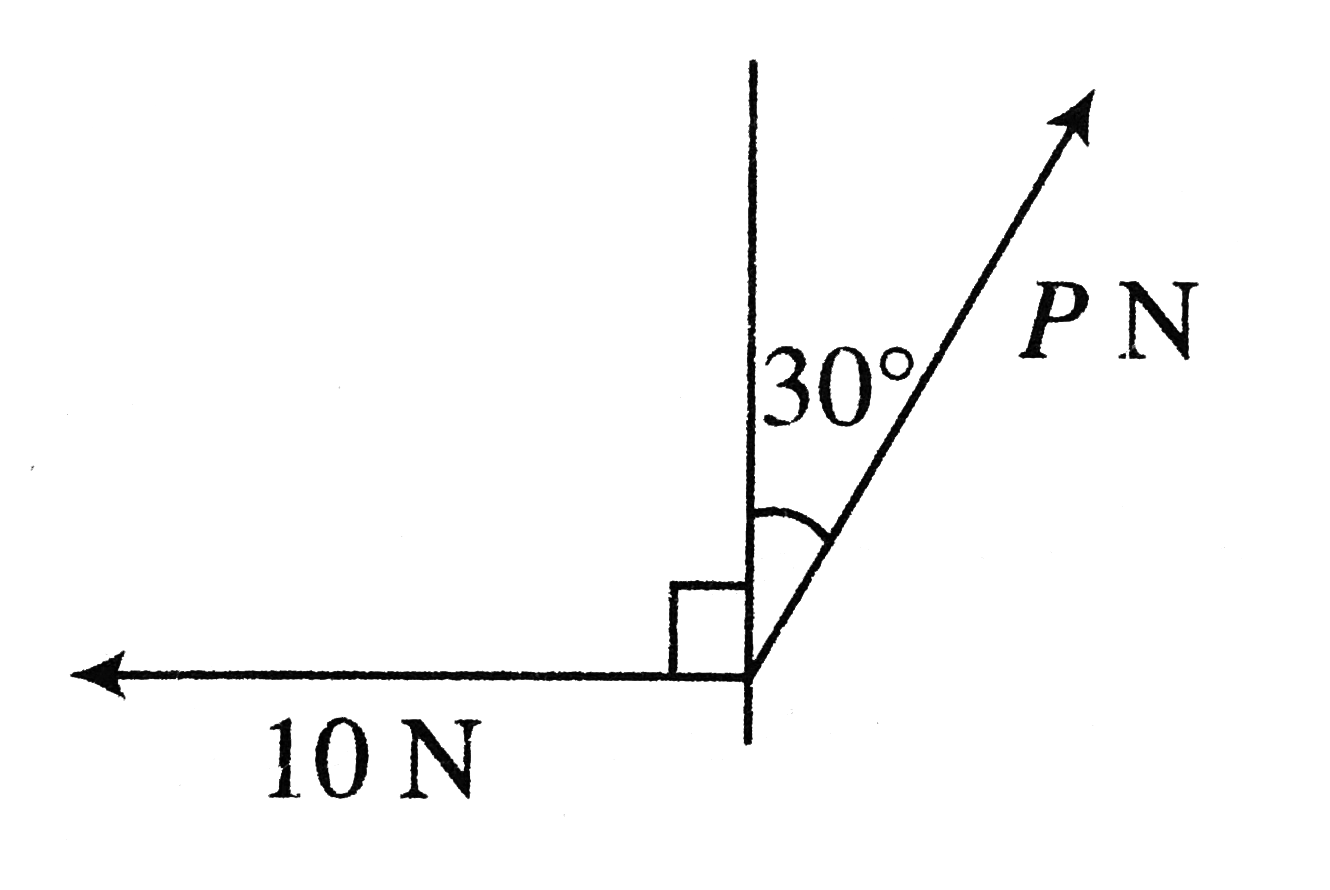
View Solution
Knowledge Check
Two forces of magnitude 1 N and 13 N resultant of magnitude 6√5N, then that is the angle between two forces.
Acos−1.113Bcos−1.513Ccos−1.135Dcos−1.137Three forces are acting on a particle as shown in the figure. To have the resultant force only along the Y-direction, the magnitude of the maximum additional force needed is
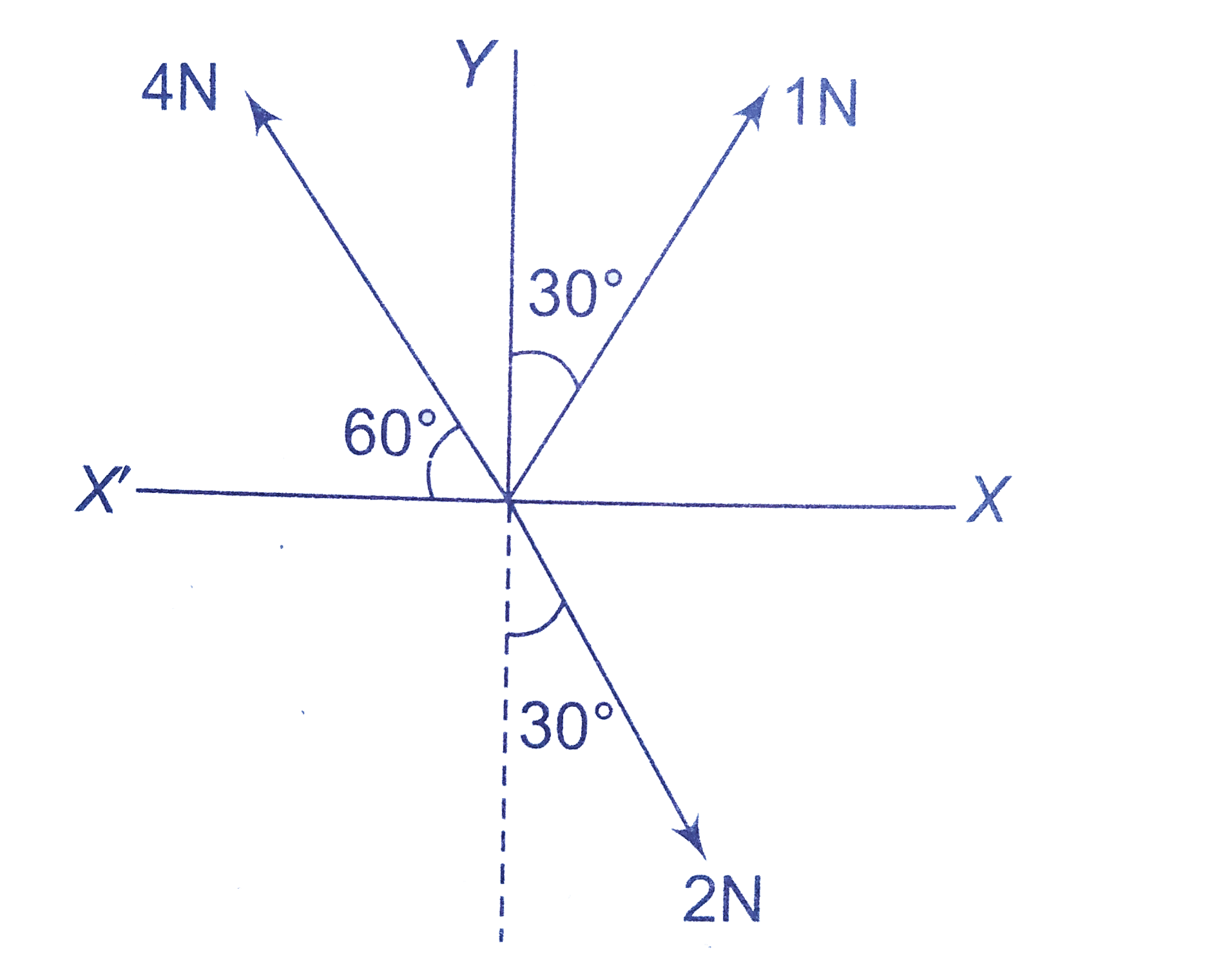 A0.866NB1.732NC0.5ND4N
A0.866NB1.732NC0.5ND4NIf two forces of 5 N each are acting along X and Y axes, then the magnitude and direction of resultant is
A5√2,π/3B5√2,π/4C−5√2,π/3D−5√2,π/4
The resultant of 2 forces of magnitude 1N and 13N is 6√5N. Find the tangent of the angle made by resultant with 1N force.
View SolutionThe magnitudes of two forces X and Y are in the ratio 2:3 . If the resultant of two forces is 25N and angle between them 60∘, find the magnitude of each force close to one place of decimal .
View SolutionThree ant P,Q and R are pulling a grain with forces of magnitude 6N,3√3N and 3√2N as shown in the figure. Find the magnitude of resultant force (in N ) acting on the grain .

View SolutionFind the angle between the plane: x−y+z=5 and x+2y+z=9
View SolutionThe two forces 2√2N and xN are acting at a point their resultant is perpendicular to ˆxN and having magnitude of √6N.The angle between the two forces and magnitude of x are.
View Solution
