The resultant of 2 forces of magnitude 1N and 13N is $6 \sqrt{5} N$ . Find the tangent of the angle made by resultant with 1N force.

Video Solution

Text Solution

Verified by Experts

Let P=1N
Q=13N ltbgt $R = 6 \sqrt{5} N$
By Parallelogram rule of vector addition
$R^{2} = P^{2} + Q^{2} + 2 P Q cos θ$
${(6 \sqrt{5})}^{2} = {(1)}^{2} + {(13)}^{2} + 2 \times 1 \times 13 cos θ$

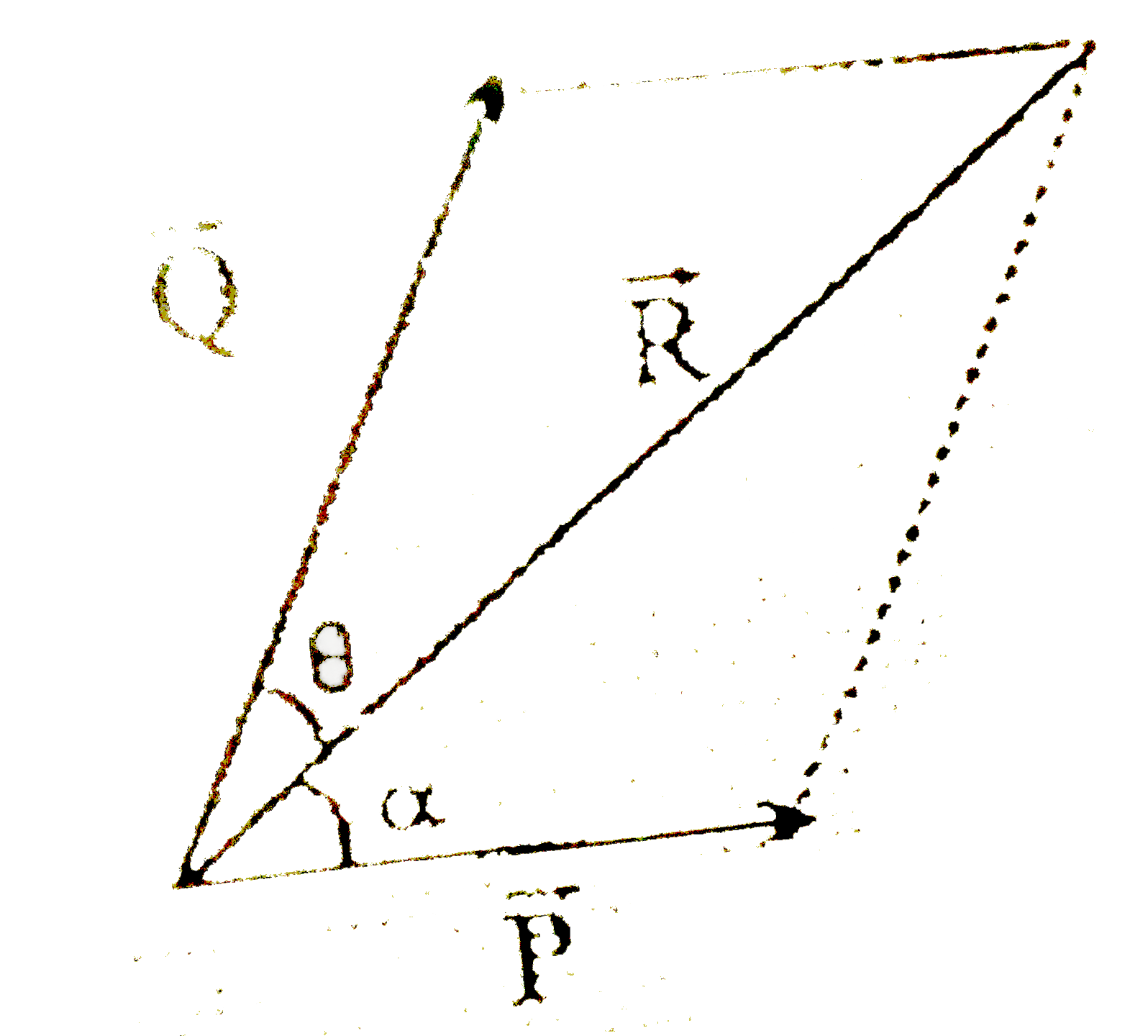
$θ = {cos}^{- 1} (\frac{5}{13})$ . . . .(1)
$tan α = \frac{Q sin θ}{P + Q cos θ} = \frac{13 sin θ}{1 + 13 cos θ}$
$\frac{13 \times \frac{12}{13}}{1 + 13 \times \frac{5}{13}} = \frac{12}{6} = 2$
$α = {tan}^{- 1} 2$ . . . .(2)
Ans. Angle between given vectors is
$θ = {cos}^{- 1} (\frac{5}{13})$
Angle of resultant with $1 N f or c e < b r >$ =alpha-tan^(-1)(2)

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The resultant force of 5 N and 10 N can not be
A12 N
B8 N
C4 N
D5 N
The resultant force of 5 N and 10 N cannot be
A12 N
B8 N
C4 N
D5 N
The resultant of two forces of 10N and 5N can never be :-
A12N
B5N
C10N
D4N

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile