A vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
The correct Answer is:8√5
To solve the problem step by step, we will use vector addition and the properties of right triangles.
1. Understanding the Vectors:
- Let the magnitude of vector →A be A (unknown).
- The magnitude of vector →B is given as 8.0.
- The resultant vector →R lies along the y-axis and has a magnitude of 2A.
2. Setting Up the Coordinate System:
- Place vector →A along the x-axis. Thus, we can represent it as →A=A^i.
- Since →B is added to →A and the resultant is along the y-axis, we can represent vector →B as →B=8^j (assuming it is in the positive y-direction).
3. Using the Pythagorean Theorem:
- The resultant vector →R can be calculated using the Pythagorean theorem since →A and →B are perpendicular to each other.
- The magnitude of the resultant vector →R is given by:
R=√A2+B2
- Substituting B=8:
R=√A2+82=√A2+64
4. Setting Up the Equation for the Resultant:
- We know that the magnitude of the resultant vector →R is also equal to 2A:
√A2+64=2A
5. Squaring Both Sides:
- To eliminate the square root, square both sides:
A2+64=(2A)2
- This simplifies to:
A2+64=4A2
6. Rearranging the Equation:
- Rearranging gives:
4A2−A2−64=0
- This simplifies to:
3A2−64=0
7. Solving for A2:
- Rearranging gives:
3A2=64
- Dividing by 3:
A2=643
8. Finding the Magnitude of A:
- Taking the square root:
A=√643=8√3
Final Answer:
The magnitude of vector →A is 8√3.
- Let the magnitude of vector →A be A (unknown).
- The magnitude of vector →B is given as 8.0.
- The resultant vector →R lies along the y-axis and has a magnitude of 2A.
- Place vector →A along the x-axis. Thus, we can represent it as →A=A^i.
- Since →B is added to →A and the resultant is along the y-axis, we can represent vector →B as →B=8^j (assuming it is in the positive y-direction).
- The resultant vector →R can be calculated using the Pythagorean theorem since →A and →B are perpendicular to each other.
- The magnitude of the resultant vector →R is given by:
R=√A2+B2
- Substituting B=8:
R=√A2+82=√A2+64
- We know that the magnitude of the resultant vector →R is also equal to 2A:
√A2+64=2A
- To eliminate the square root, square both sides:
A2+64=(2A)2
- This simplifies to:
A2+64=4A2
- Rearranging gives:
4A2−A2−64=0
- This simplifies to:
3A2−64=0
- Rearranging gives:
3A2=64
- Dividing by 3:
A2=643
- Taking the square root:
A=√643=8√3
The magnitude of vector →A is 8√3.
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Single Correct
Explore 51 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
Vector →A, which is directed along an x axis , is to be added to vector →B, which has a magnitude of 7.0m. The sum is a third vector that is directed along the y axis, with a magnitude that is 3.0 times that of →A. What is that magnitude of →A ?
View SolutionVector →A, which is directed along an x axis, is to be added to vector →B, which has a magnitude of 6.0 m. The sum is a third vector that is directed along the y axis, with a magnitude of →AFind the magnitude of →A ?
View Solution
Knowledge Check
A vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
A√10B10C5D√5A vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
A4jB−4iC−(i+j)D(j+k)If →i and →j are unit vectors along x-axis and y-axis respectively, the magnitude of vector →i+→j will be :-
A1B√2C√3D2
If the resultant of →a and →b lie along y-axis. Find thre magnitude of b
View SolutionA vector vec Awhenadded→the→−−→r vec B = 3. 0 hat i+ 4 hat jyieldsarestant–––––→−−→rtˆis∈thepositivey−directionandhasamagn∫udeequal→tˆof vec B.F∈dthemagnitudeof vec A .
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
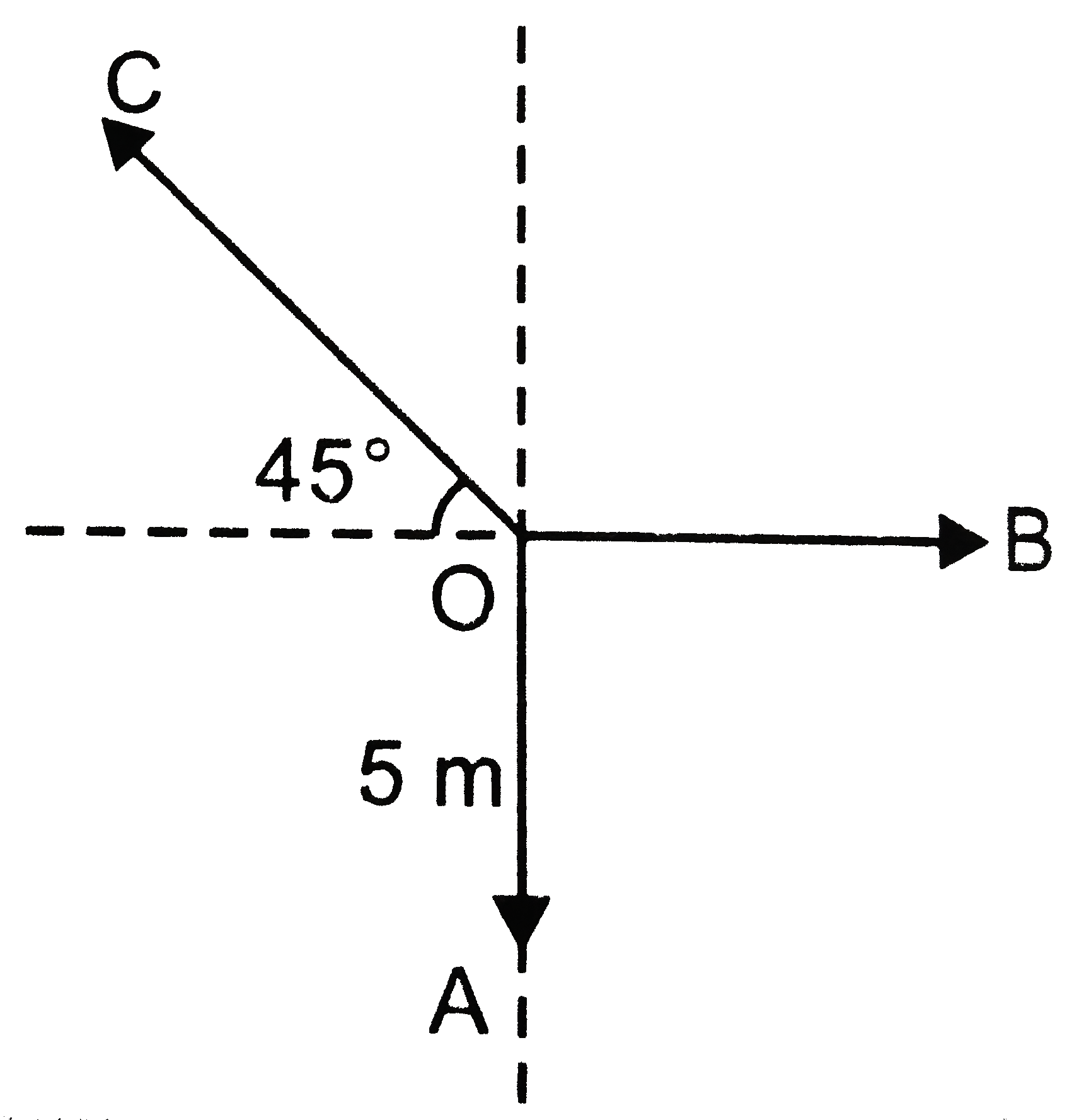 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
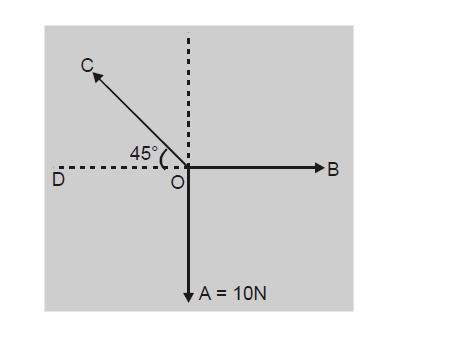
(ii) What is the magnitude of vector −−→OC ?
View SolutionWrite the magnitude of the vector →a in terms of dot product.
View Solution

