100 coplanar forces each equal to 10 N act on a body. Each force makes angle with the preceding force. What is the resultant of the forces
1000N
500N
250N
zero
The correct Answer is:D
To solve the problem of finding the resultant of 100 coplanar forces, each equal to 10 N and making an angle of π50 radians with the preceding force, we can follow these steps:
Step 1: Understand the Configuration of Forces
We have 100 forces acting on a body, each with a magnitude of 10 N. Each force is separated by an angle of π50 radians from the preceding force. This means that the forces are arranged in a circular manner around a point.
Step 2: Calculate the Total Angle
The total angle formed by the 100 forces can be calculated as:
Total Angle=Number of Forces×Angle between Forces=100×π50=2π
This indicates that the forces complete a full circle.
Step 3: Analyze the Resultant of the Forces
When forces are arranged in such a way that they complete a full circle (i.e., the total angle is 2π), they form a closed polygon. In this case, since the forces are evenly distributed around a point, they will cancel each other out.
Step 4: Conclusion
Since the forces form a closed polygon, the resultant of all these forces is zero. Therefore, the resultant force acting on the body is:
Resultant=0N
Final Answer
The resultant of the forces is 0N.
---
We have 100 forces acting on a body, each with a magnitude of 10 N. Each force is separated by an angle of π50 radians from the preceding force. This means that the forces are arranged in a circular manner around a point.
The total angle formed by the 100 forces can be calculated as:
Total Angle=Number of Forces×Angle between Forces=100×π50=2π
This indicates that the forces complete a full circle.
When forces are arranged in such a way that they complete a full circle (i.e., the total angle is 2π), they form a closed polygon. In this case, since the forces are evenly distributed around a point, they will cancel each other out.
Since the forces form a closed polygon, the resultant of all these forces is zero. Therefore, the resultant force acting on the body is:
Resultant=0N
The resultant of the forces is 0N.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Fill in the blanks type
Explore 26 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Comprehension Type
Explore 31 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Multiple Correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
12 forces each equal to P act on a body. reach force make angle of 30 with the next one, the resultant of all the forces is ?
View SolutionWe have n coplanar forces, each of magnitude T. If each force makes an angle 2πn with the preceding force, then the vector sum of the n forces is a null vector.
View Solution
Knowledge Check
Eleven forces each equal to 5N act on a particle simultaneously.If each force makes an angle 30∘ with the next one, the resultant of all forces is
A15NB55NC5NDzeroTwo forces, each equal to F, act as shown in figure. Their resultant is
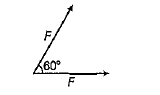 AF/2BFC√3D√5F
AF/2BFC√3D√5FFive equal forces each of 20N are acting at a point in the same plane. If the angles between them are same, the resultant of these forces is
A0B40NC20ND20√2N
Find the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
View SolutionFind the vector sum of N coplanar forces, each of the magnitude F,when each force makes an angle of 2π/N with that preceding it.
View SolutionTwo forces 10 N and 15 N are acting on a body then which cannot be the resultant of these two forces
View SolutionTwo forces, each equal to F, act as shown in (figure) Their resultant is
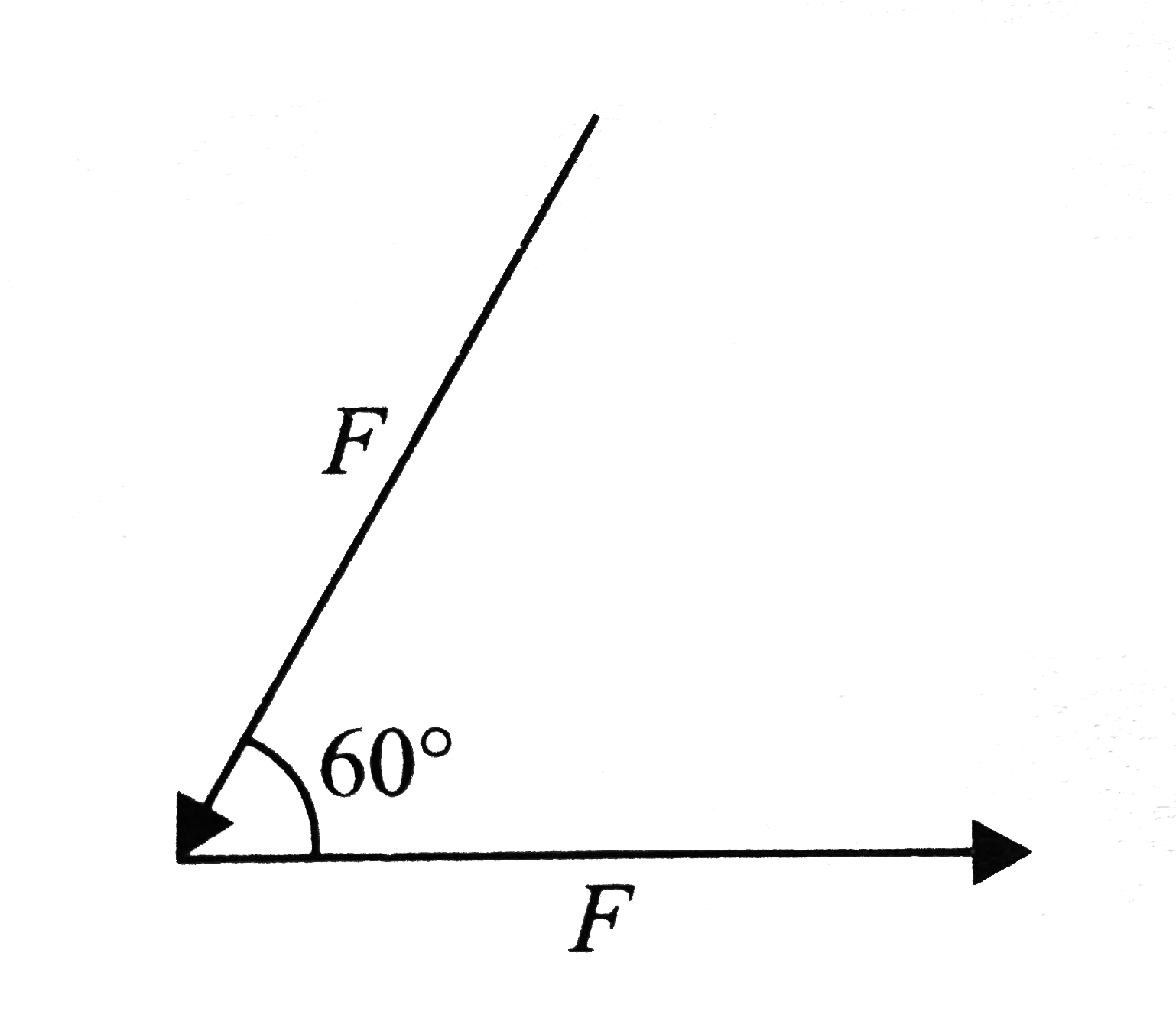
View SolutionA force of 20 N acts on a body and the body moves through 1 m at an angle of45∘ in the direction of the force. The work done by the force is
View Solution