In the figure, M is the midpoint of QR. ∠PRQ=90∘. Prove that PQ2=4PM2−3PR2
To prove that PQ2=4PM2−3PR2 given that M is the midpoint of QR and ∠PRQ=90∘, we will follow these steps:
Step 1: Identify the triangles
Since M is the midpoint of QR, we have RM=MQ. We also know that ∠PRQ=90∘, which allows us to apply the Pythagorean theorem in triangle PRQ.
Step 2: Apply the Pythagorean theorem to triangle PRQ
Using the Pythagorean theorem:
PQ2=PR2+QR2
Step 3: Analyze triangle PRM
In triangle PRM, we can apply the Pythagorean theorem again:
PR2=PM2+RM2
Step 4: Express RM in terms of QR
Since M is the midpoint of QR, we have:
RM=QR2
Thus, we can substitute RM into the equation from Step 3:
PR2=PM2+(QR2)2
This simplifies to:
PR2=PM2+QR24
Step 5: Rearranging the equation
Rearranging the equation gives us:
PM2=PR2−QR24
Step 6: Substitute QR2 back into the equation for PQ2
From Step 2, we have:
PQ2=PR2+QR2
Now substituting QR2 from our previous equation:
QR2=4(PM2−PR2)
Substituting this into the equation for PQ2:
PQ2=PR2+4(PM2−PR2)
This simplifies to:
PQ2=PR2+4PM2−4PR2
PQ2=4PM2−3PR2
Conclusion
Thus, we have proved that:
PQ2=4PM2−3PR2
Since M is the midpoint of QR, we have RM=MQ. We also know that ∠PRQ=90∘, which allows us to apply the Pythagorean theorem in triangle PRQ.
Using the Pythagorean theorem:
PQ2=PR2+QR2
In triangle PRM, we can apply the Pythagorean theorem again:
PR2=PM2+RM2
Since M is the midpoint of QR, we have:
RM=QR2
Thus, we can substitute RM into the equation from Step 3:
PR2=PM2+(QR2)2
This simplifies to:
PR2=PM2+QR24
Rearranging the equation gives us:
PM2=PR2−QR24
From Step 2, we have:
PQ2=PR2+QR2
Now substituting QR2 from our previous equation:
QR2=4(PM2−PR2)
Substituting this into the equation for PQ2:
PQ2=PR2+4(PM2−PR2)
This simplifies to:
PQ2=PR2+4PM2−4PR2
PQ2=4PM2−3PR2
Thus, we have proved that:
PQ2=4PM2−3PR2
Topper's Solved these Questions
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:3.5 (4 mark each)
Explore 4 Videos
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:Assignment 3.1
Explore 8 Videos
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:3.3 (2 mark each)
Explore 8 Videos
- PROBABILITY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY Exercise:ASSIGNEMENT 5.4
Explore 12 Videos
- QUADRATIC EQUATION Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATION Exercise:CHALLENGIN QUESTIONS
Explore 2 Videos
Similar Questions
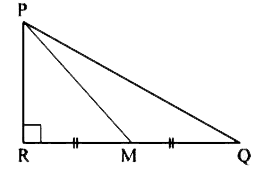
In the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
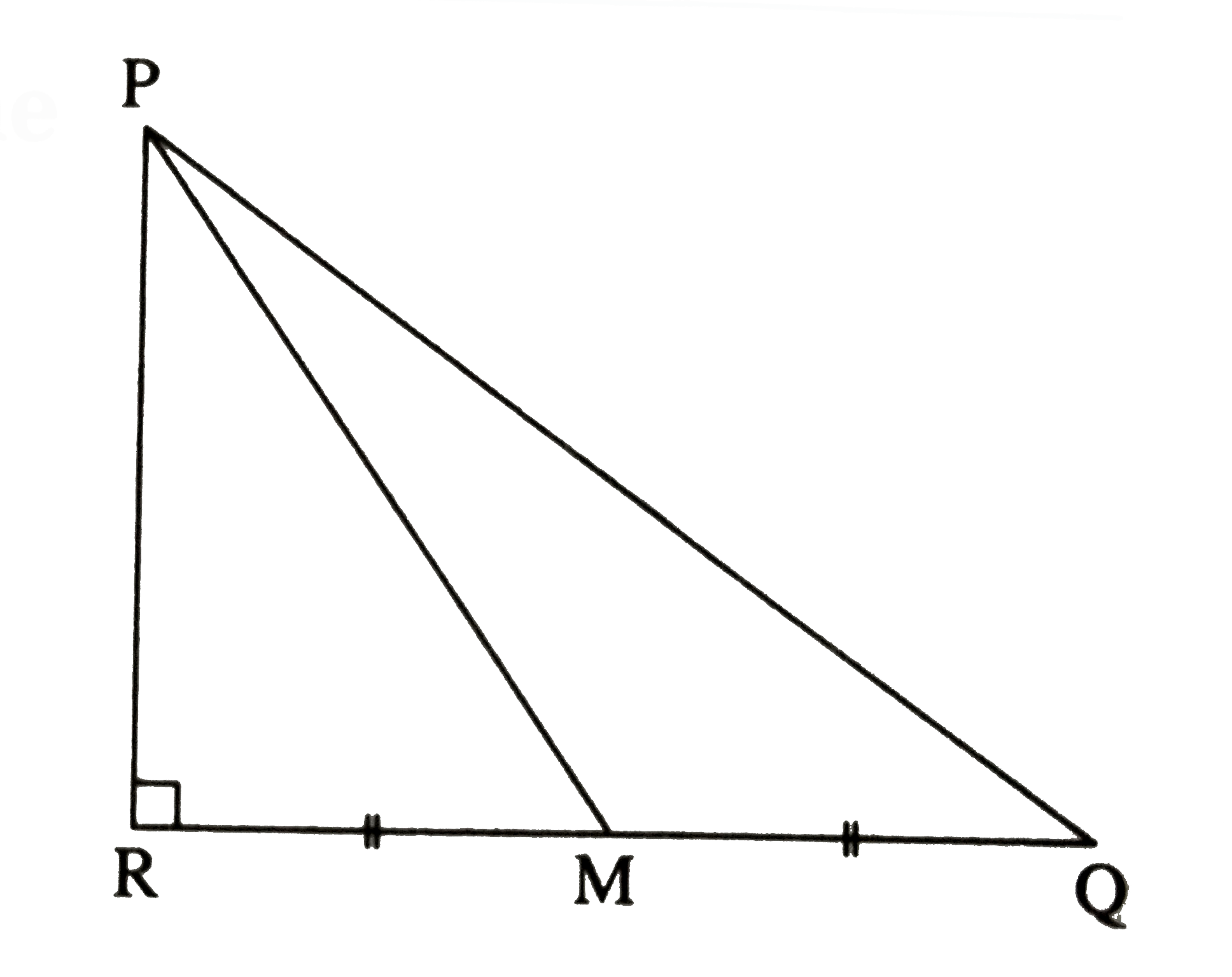
View SolutionIn the figure , M is the midpoint of QR .
∠PRQ=90∘.
Prove that ,
PQ2=4PM2−3PR2 .
View SolutionIn adjoining figure, seg PS is the median of ΔPQRadnPT⊥QR. Prove that
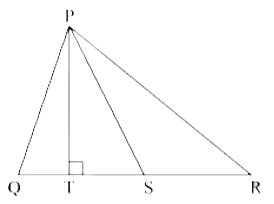
(1) PR2=PS2+QR×ST+(OR2)2
(2) PQ2=PS2+QR×ST+(QR2)2
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
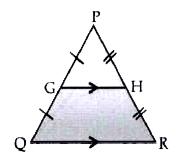
View SolutionIn the given figure G is the mid-point of the side PQ of ΔPQR and GH || QR .Prove that H is the mid -point of the side PR of the triangle PQR .
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

View Solution1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
View SolutionIn the figure given below, ΔPQR is right-angled at Q and the points S and T trisect the side QR. Prove that 8PT2=3PR2+5PS2
View SolutionIn the figure in ∠PQR=∠PRQ then prove that ∠PQS=∠PRT
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View Solution

