In the figure, ∠DFE=90∘, seg FG⊥ side DE, DG=8, FG=12 then complete the following activity to find the length of seg DE.
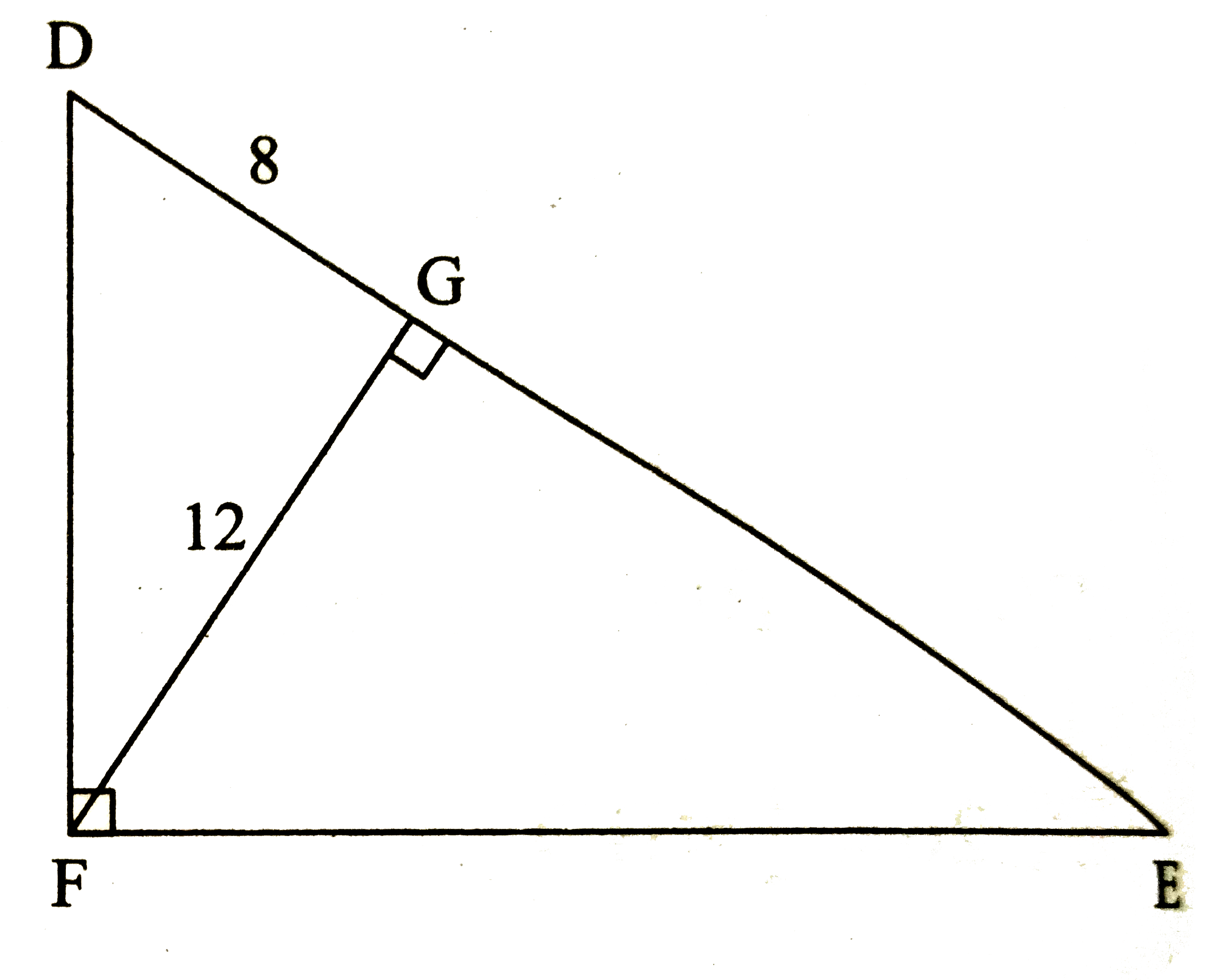
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=□×EG
∴122=□×EG
EG=12×12□
∴EG=□
DE=DG+GE=8+□=□
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=DG×EG
∴122=8×EG
EG=12×128
∴EG=18
DE=DG+GE=8+18=26
Topper's Solved these Questions
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:3.5 (4 mark each)
Explore 4 Videos
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:Assignment 3.1
Explore 8 Videos
- PYTHAGORAS THEOREMBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PYTHAGORAS THEOREMExercise:3.3 (2 mark each)
Explore 8 Videos
- PROBABILITY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY Exercise:ASSIGNEMENT 5.4
Explore 12 Videos
- QUADRATIC EQUATION Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUADRATIC EQUATION Exercise:CHALLENGIN QUESTIONS
Explore 2 Videos
Similar Questions
In the figure, ∠LMN=∠LKN=90∘
seg MK⊥ seg LN.
Complete the following activity to prove R is the midpoint of seg MK.
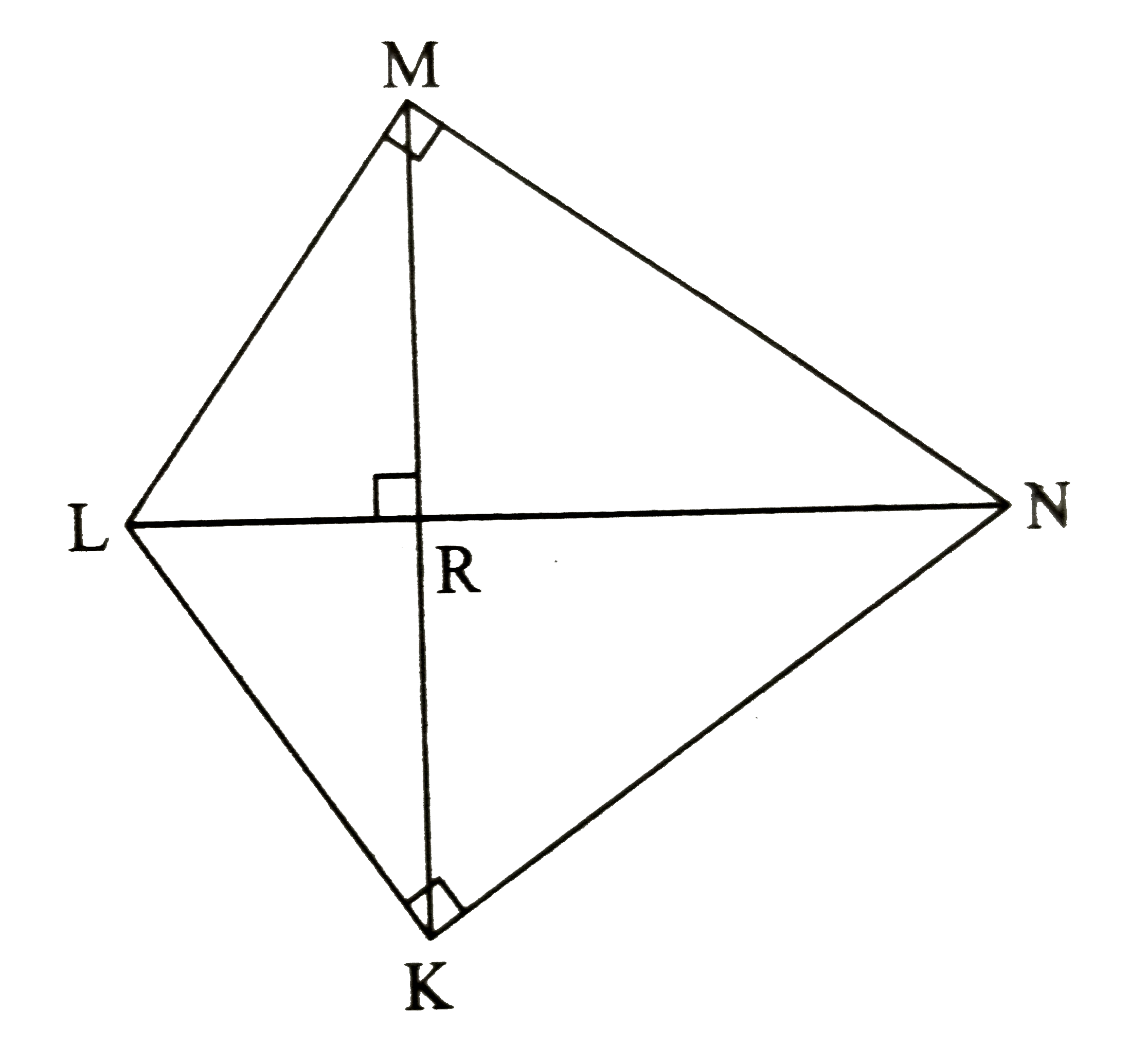
Proof: In ΔLMN, ∠LMN=90∘
seg MR⊥ hypotenuse LN
∴ by property of geometric mean,
MR2=□×RN
In ΔLKN, ∠LKN=90∘
seg KR⊥ hypotenuse LN
∴ by property of geometric mean,
KR2=LR×□
From (1) and (2), we get
MR2=□∴MR=□.
∴R is the midpoint of seg MK.
View Solution∠DFE=90∘,FG⊥ED,IFGD=8,FG=12, find (1) EG (2) FD (3) EF
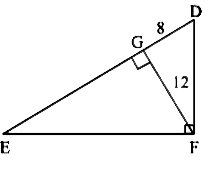
View SolutionIn the adjoining figure, ∠DFE=90∘,FG⊥ED.IfGD=8,FG=12,find
(i) EG
(ii) FD, and
(iii) EF
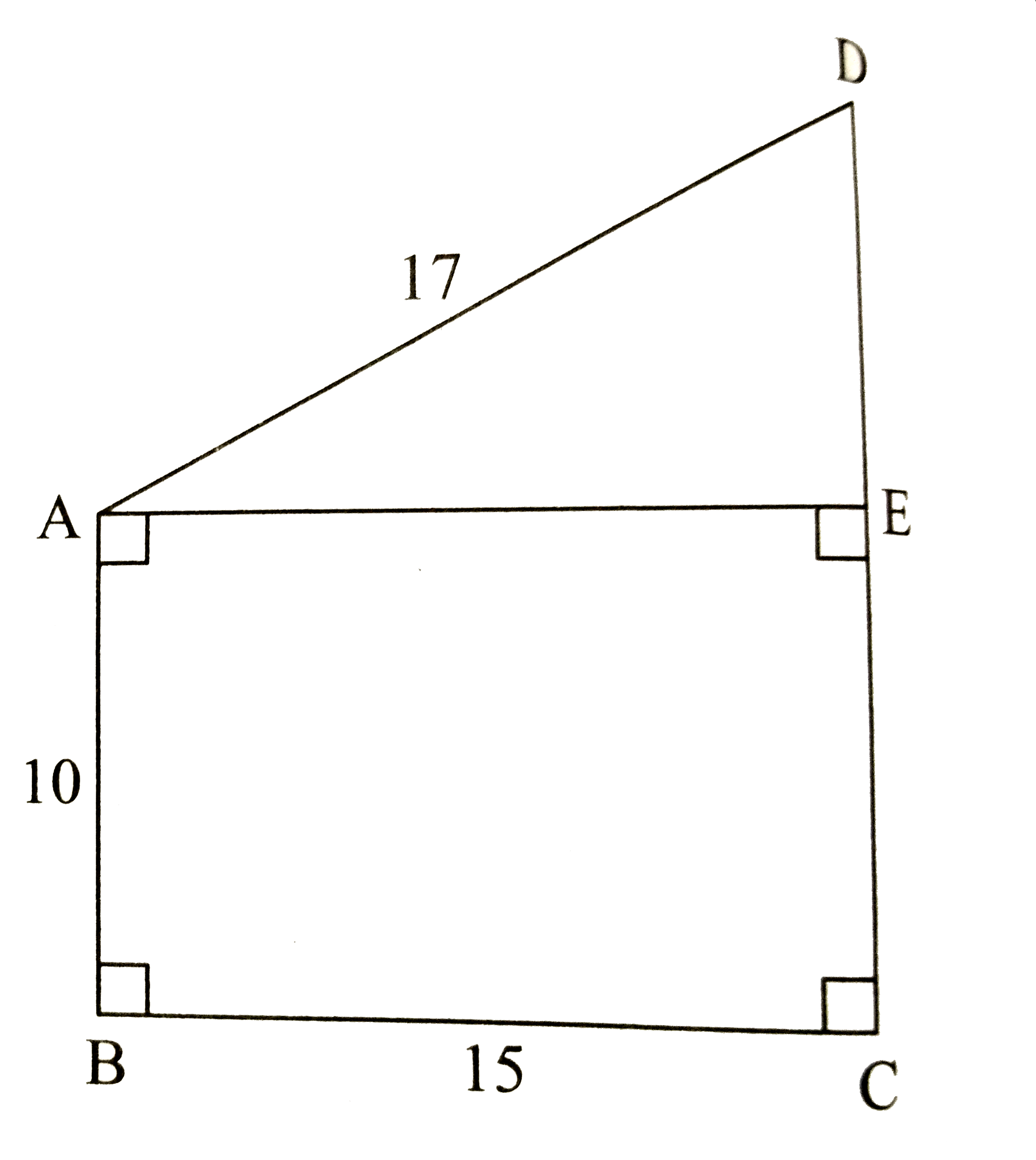
View SolutionIn the figure, AD=17, AB=10, BC=15. ∠ABC=∠BCD=90∘ seg AE⊥ side CD then find the length of (i)AE (ii)DE (iii)DC.
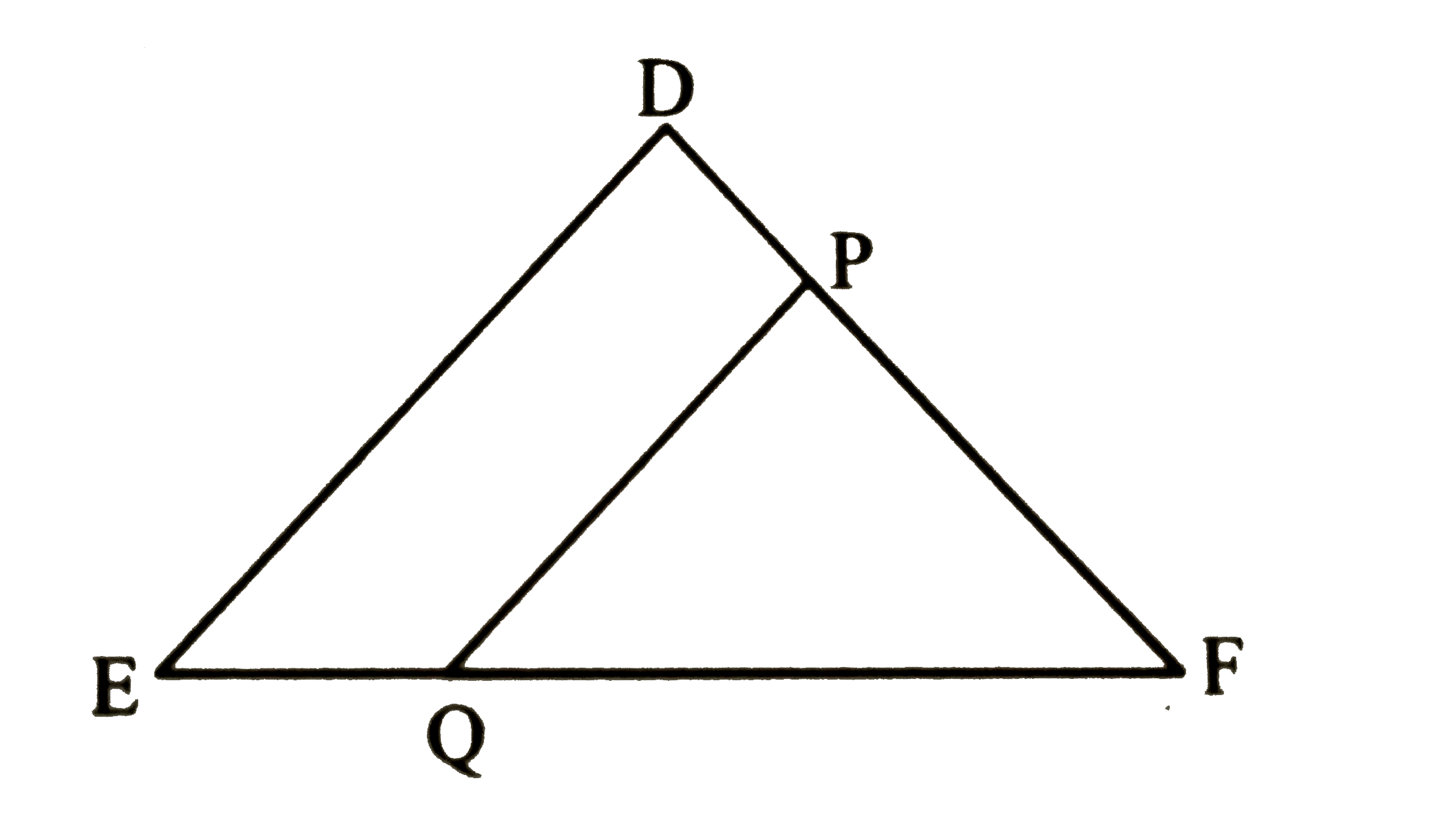
View SolutionIn the adjoining figure, seg PQ||seg DE, A(ΔPQF)=20 sq. uints, PF = 2 DP, then find A (□DPQE) by completing the following activity.
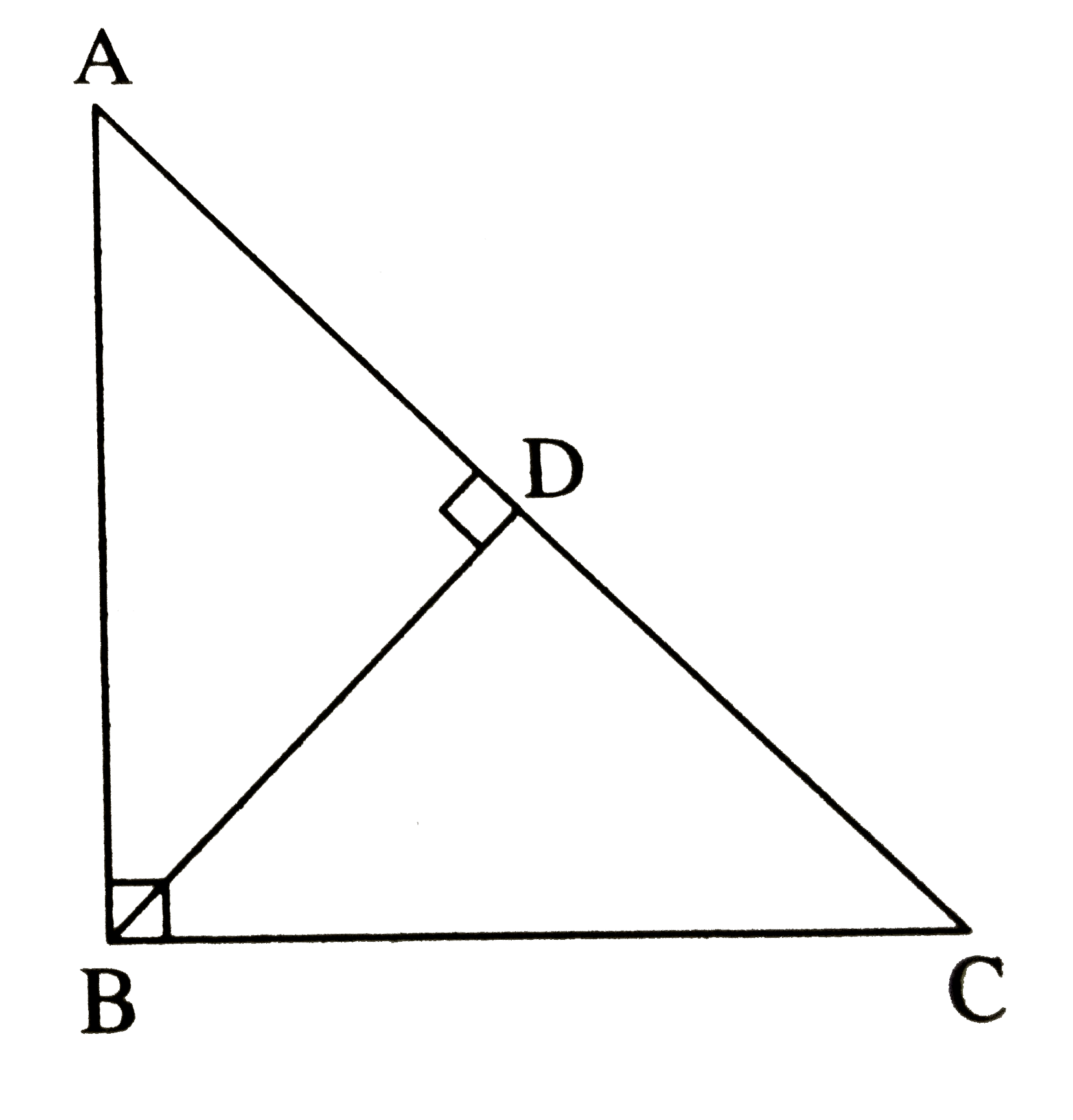
View SolutionIn the figure, ∠ABC=90∘ and seg Bd⊥ side AC, A−D−C then by property of geometric mean. BD2=□×□. Fill in the boxes with the correct answer.
View Solution(A) Complete any two out of three activites :
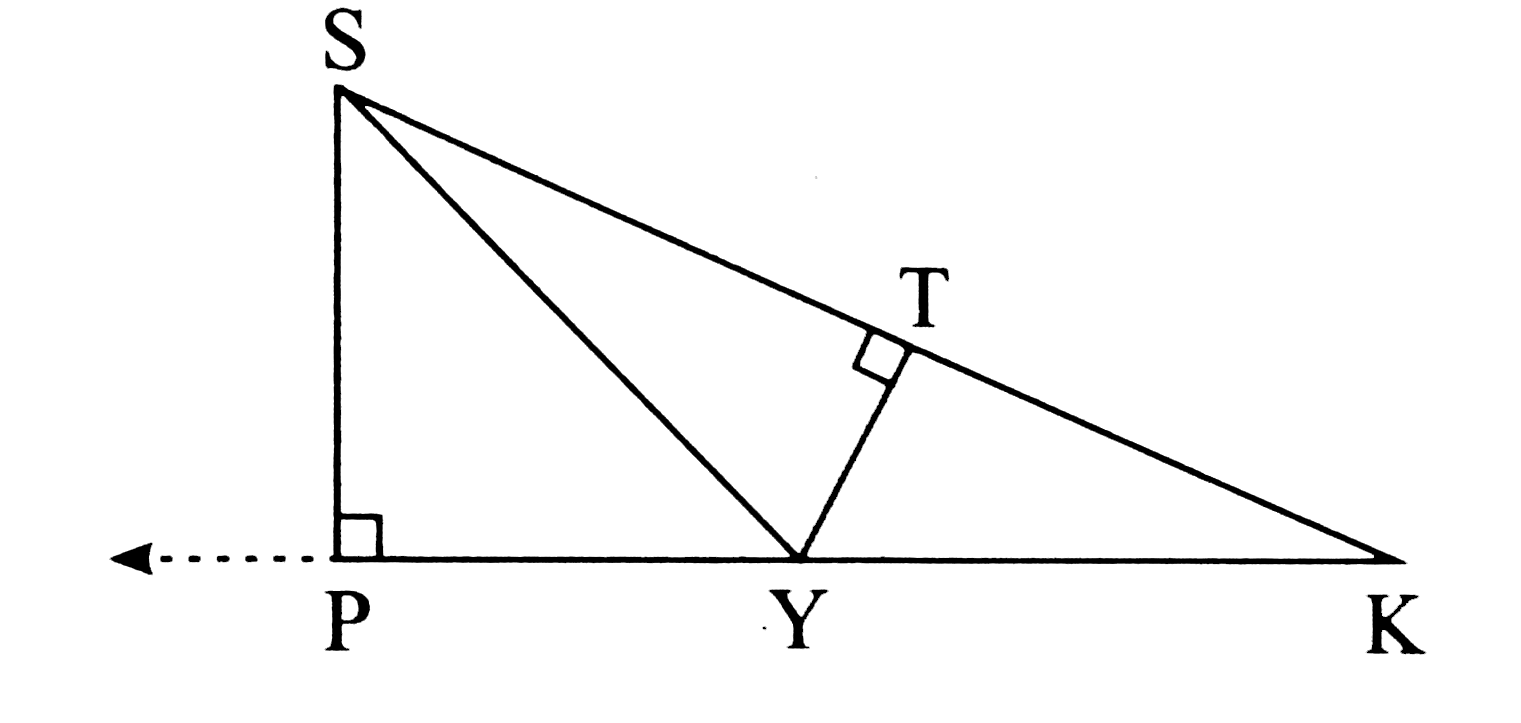 In the figure , seg SP ⊥ side YK . Seg YT⊥ side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A(ΔSYK):A(ΔYTK)
In the figure , seg SP ⊥ side YK . Seg YT⊥ side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A(ΔSYK):A(ΔYTK)
The ratio of the areas of the two Deltas is equal to the ratio of the products of their □ and the corresponding heights
∴A(ΔSYK)A(ΔYTK)=□×SPTK×TY
=13×612×□
=□□
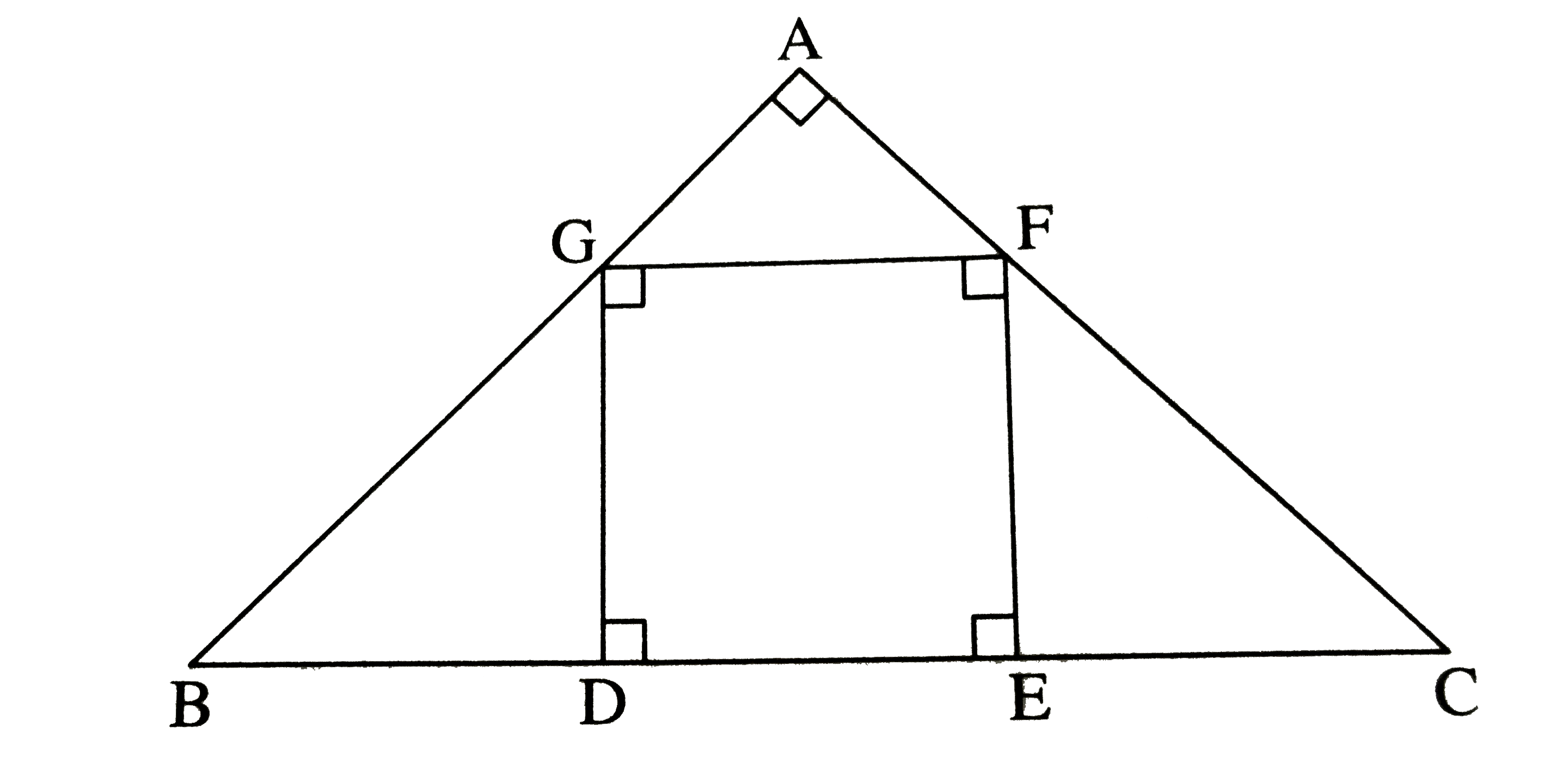
View SolutionIn figure, the vertices, of square DEFG are on the sides of ΔABC. ∠A=90∘. Then prove that DE2=BD×EC.
View SolutionIn the figure, AC=8cm, ∠ABC=90∘. ∠BAC=60∘, ∠ACB=30∘. Complete the following activity to find AB and BC.
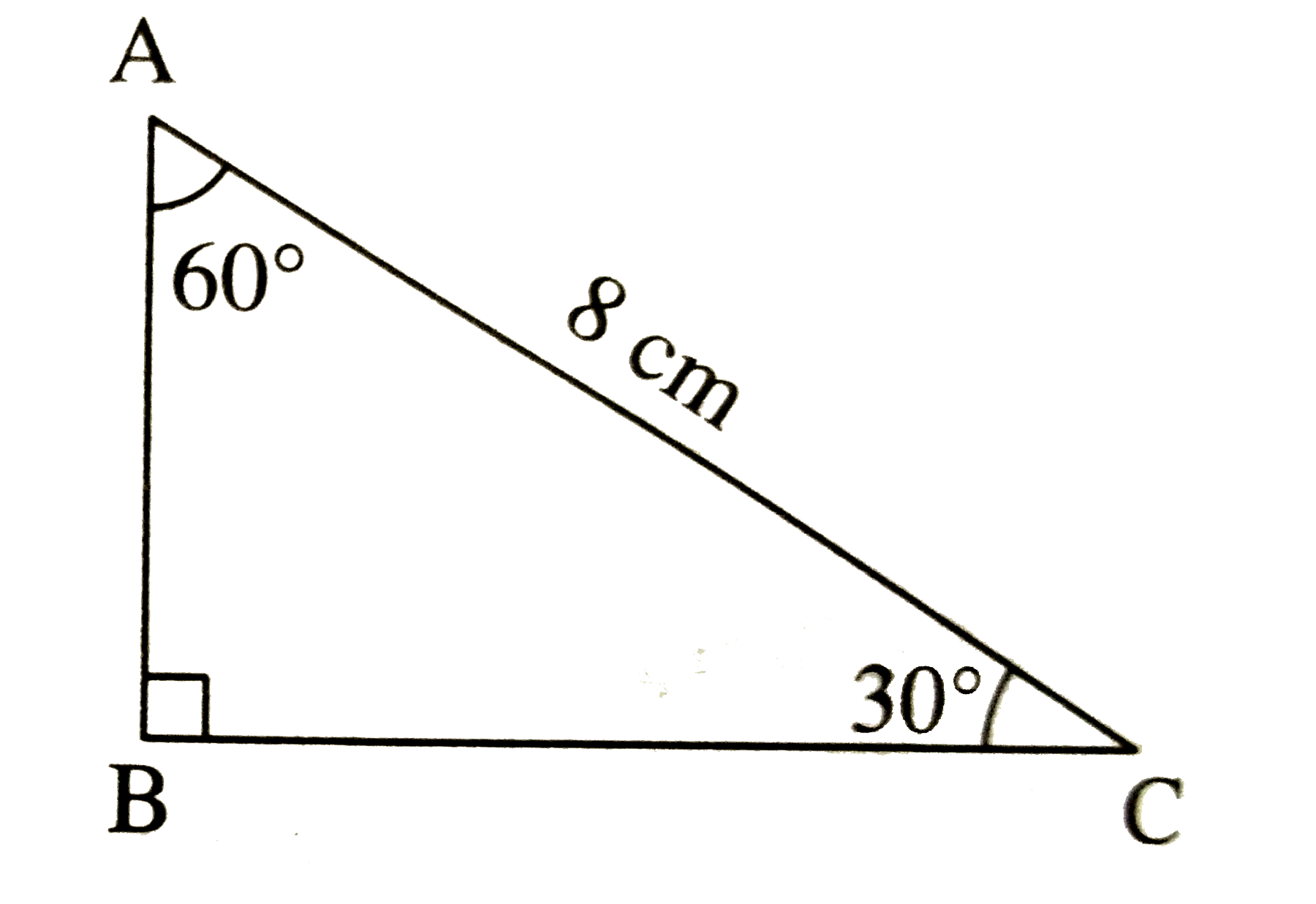
In ΔABC,
By 30∘−60∘−90∘ triangle theorem,
∴AB=12×AC and BC=−AC
∴AB=12×8 and BC=−×8
∴AB=□cm and BC=□cm
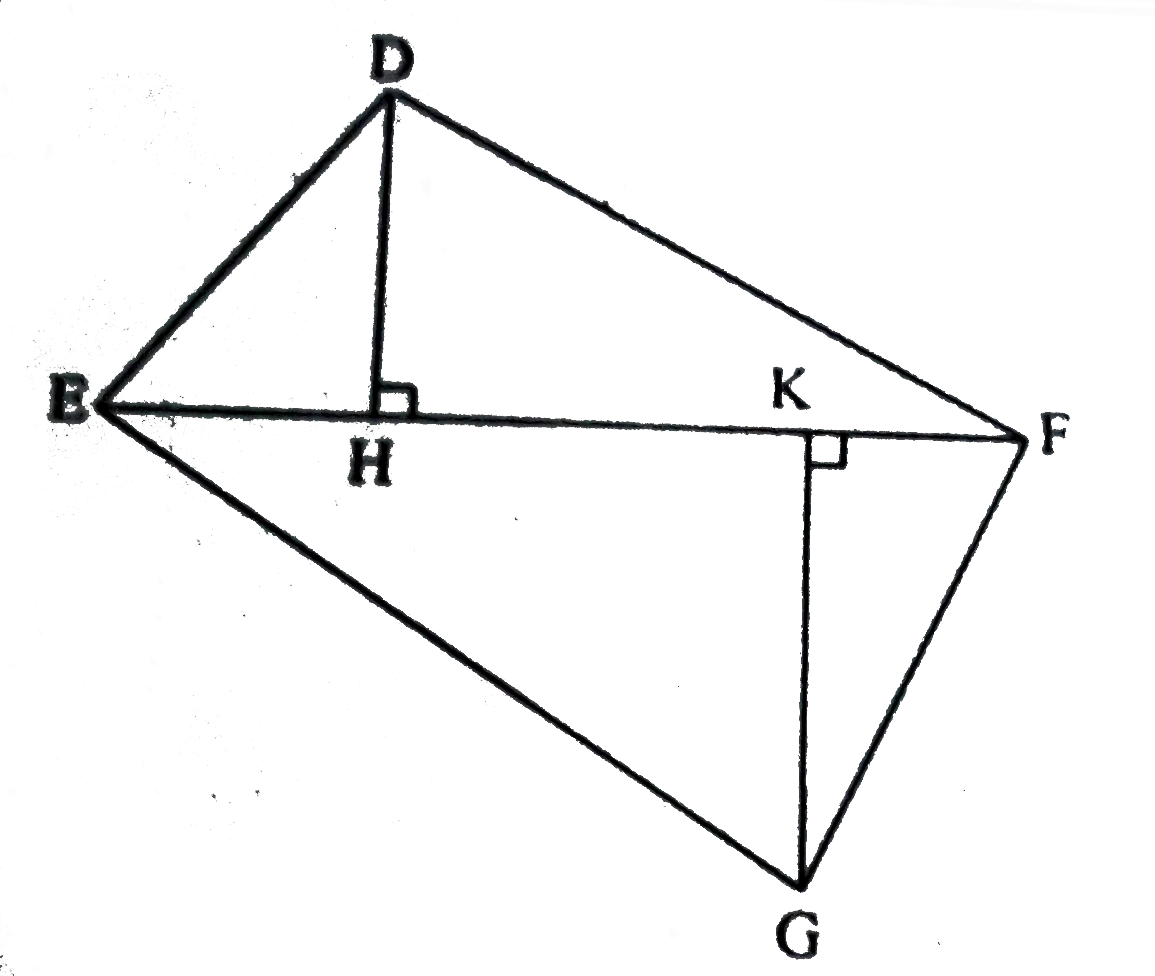
View SolutionIn the following figure,segDH⊥segEFandsegGK⊥segEF.IfDH=6cm,GK=10cmandA(ΔDEF)=150cm2, then find :
i.EF
ii.A(ΔGEF)
iii.A(□DFGE).
View Solution

