In the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

Step by step video & image solution for In the given figure, seg PM is a median of DeltaPQR.PM=9andPQ^(2)+PR^(2)=290, then find QR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Chapter Assessment
Explore 16 Videos
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Aditional Problems for Practice(Based on the Practice Set 2.1)
Explore 23 Videos
- PROBABILITYBook:TARGET PUBLICATIONChapter:PROBABILITYExercise:Try This
Explore 1 Video
- QUADRATIC EQUATIONSBook:TARGET PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:Additional problems for Practice : Based on Practice set 2.6
Explore 30 Videos
Similar Questions
Knowledge Check
In the given figure , ΔABC~ΔPQR ,PM is median of ΔPQR . If ar (ΔABC)=289cm2,BC=17cm,MR=6.5cm , then the area of ΔPQM is
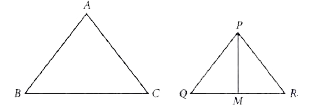 A169cm2B13cm2C84.5cm2D144.5cm2
A169cm2B13cm2C84.5cm2D144.5cm2
Seg PM is a median of ΔPQR.IFPQ=40,PR=42andPM=29, find QR.
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionSeg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
View SolutionIn the adjoing figure, seg PS is the median of ΔPQRand PT⊥QR.
i. PR2=PS2+QR×ST+(QR2)2
View SolutionIn adjoining figure, seg PS is the median of ΔPQRadnPT⊥QR. Prove that
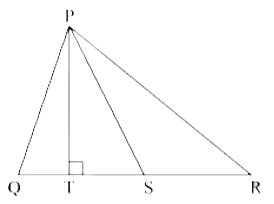
(1) PR2=PS2+QR×ST+(OR2)2
(2) PQ2=PS2+QR×ST+(QR2)2
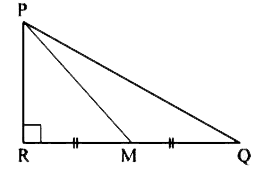
View SolutionIn the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
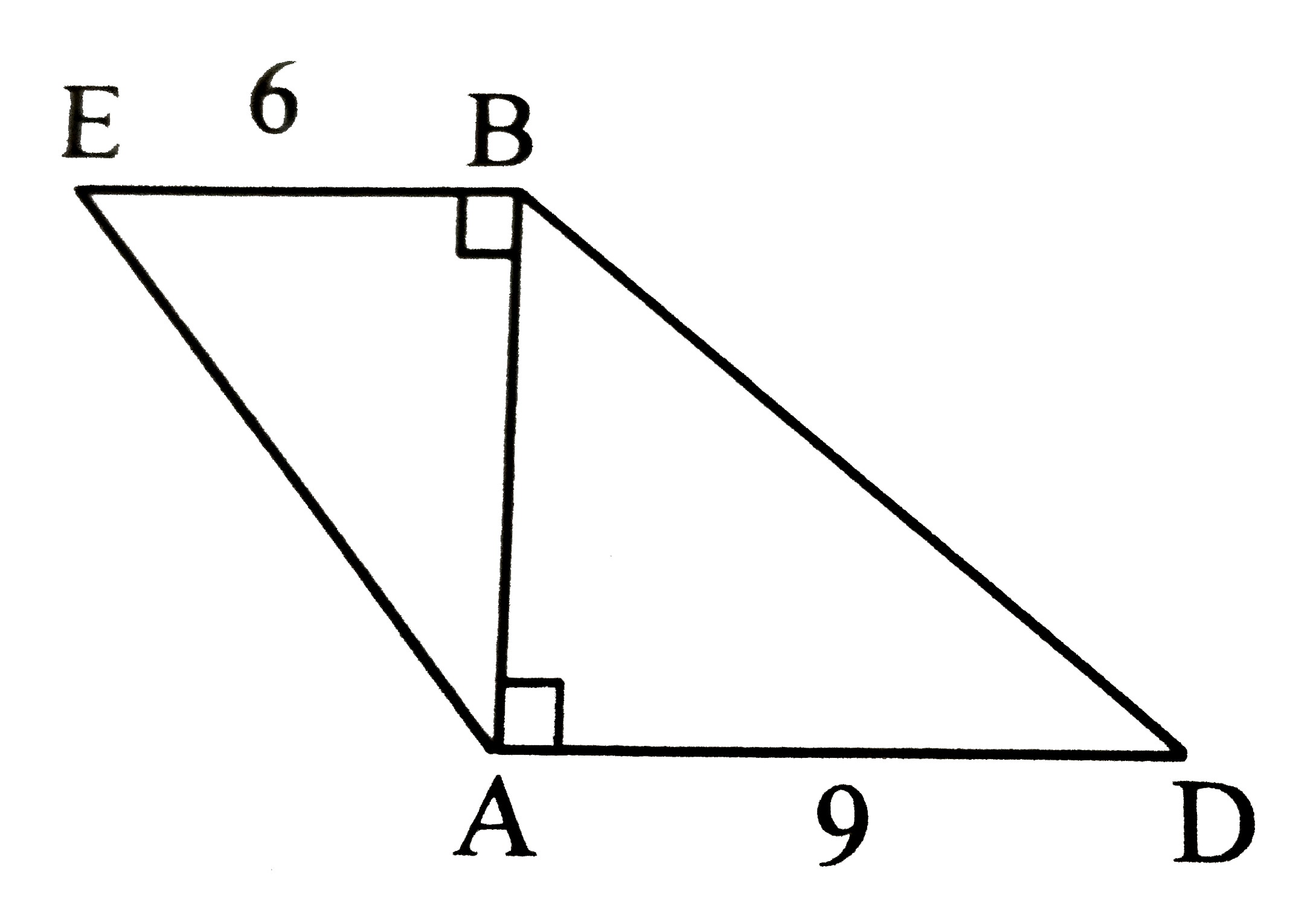
View SolutionIn the given figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and AD = 9, then find A(ΔABE)A(ΔBAD).
View Solution

