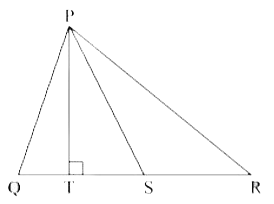
In the adjoing figure, seg PS is the median of ΔPQRand PT⊥QR.
i. PR2=PS2+QR×ST+(QR2)2
The correct Answer is:∴PQ2=PS2−QRXXST+(QR2)2
Step by step video, text & image solution for In the adjoing figure, seg PS is the median of DeltaPQRand PTbotQR. i. PR^(2)=PS^(2)+QRxxST+((QR)/(2))^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Practice Set 2.5
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Practice Set 2.6
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Practice Set 2.3
Explore 1 Video
- PROBABILITYBook:TARGET PUBLICATIONChapter:PROBABILITYExercise:Try This
Explore 1 Video
- QUADRATIC EQUATIONSBook:TARGET PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:Additional problems for Practice : Based on Practice set 2.6
Explore 30 Videos
Similar Questions
Knowledge Check
In the given figure, PS is the median, bisecting angle P, then ∠QPS is
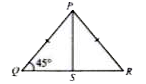 A110∘B70∘C45∘D55∘
A110∘B70∘C45∘D55∘
In the adjoining figure, PQ=PR. Show that PS>PQ.
View SolutionSeg Pm is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.
View SolutionSeg PM is a median of ΔPQR.IFPQ=40,PR=42andPM=29, find QR.
View SolutionSeg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
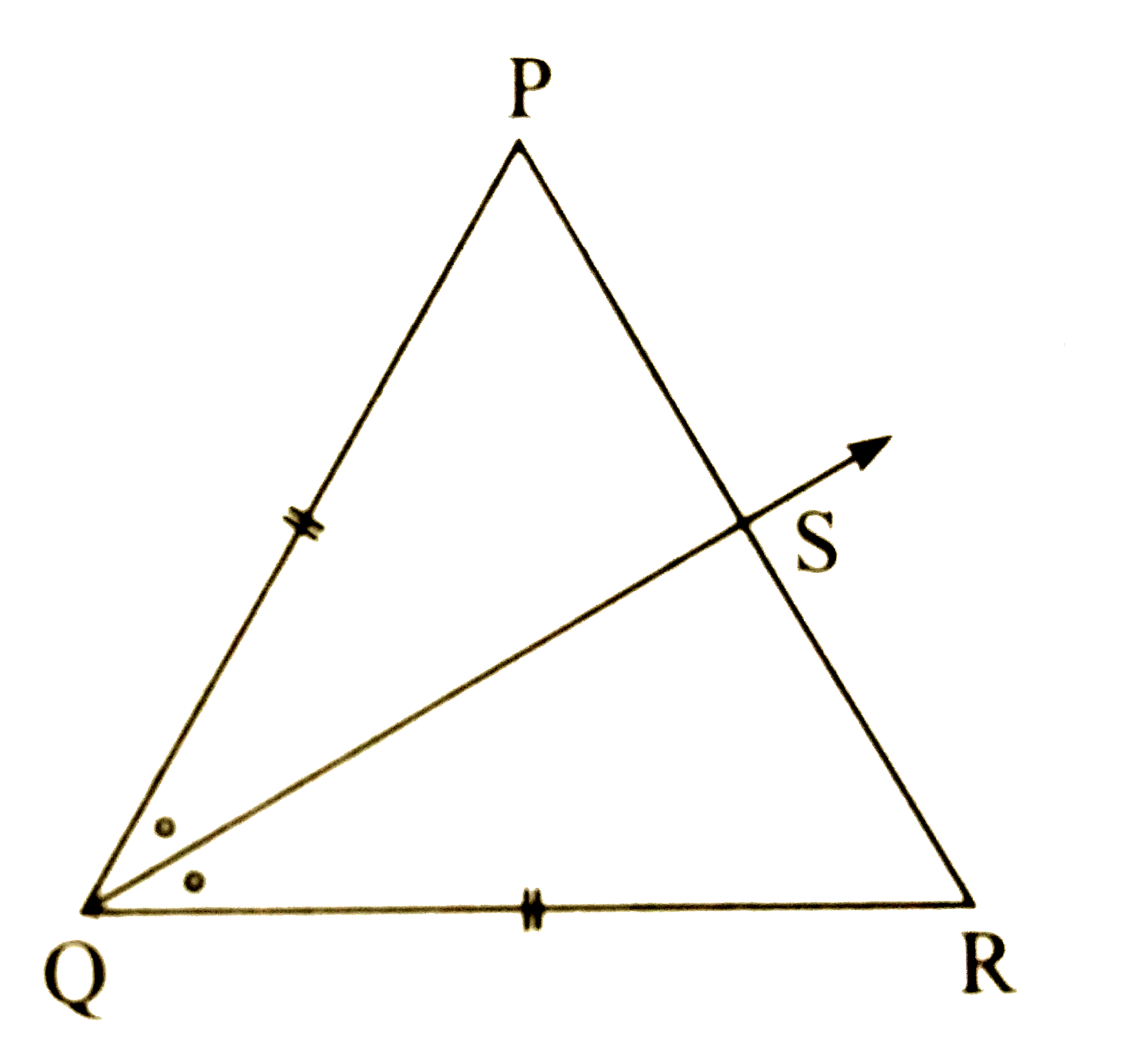
View SolutionIn the figure, ray QS is the bisector of ∠PQR and PQ=QR.
Then PSSR=………..
View SolutionIn the adjoining figure , if PQ=6,QR=10,PS=8 , find TS.
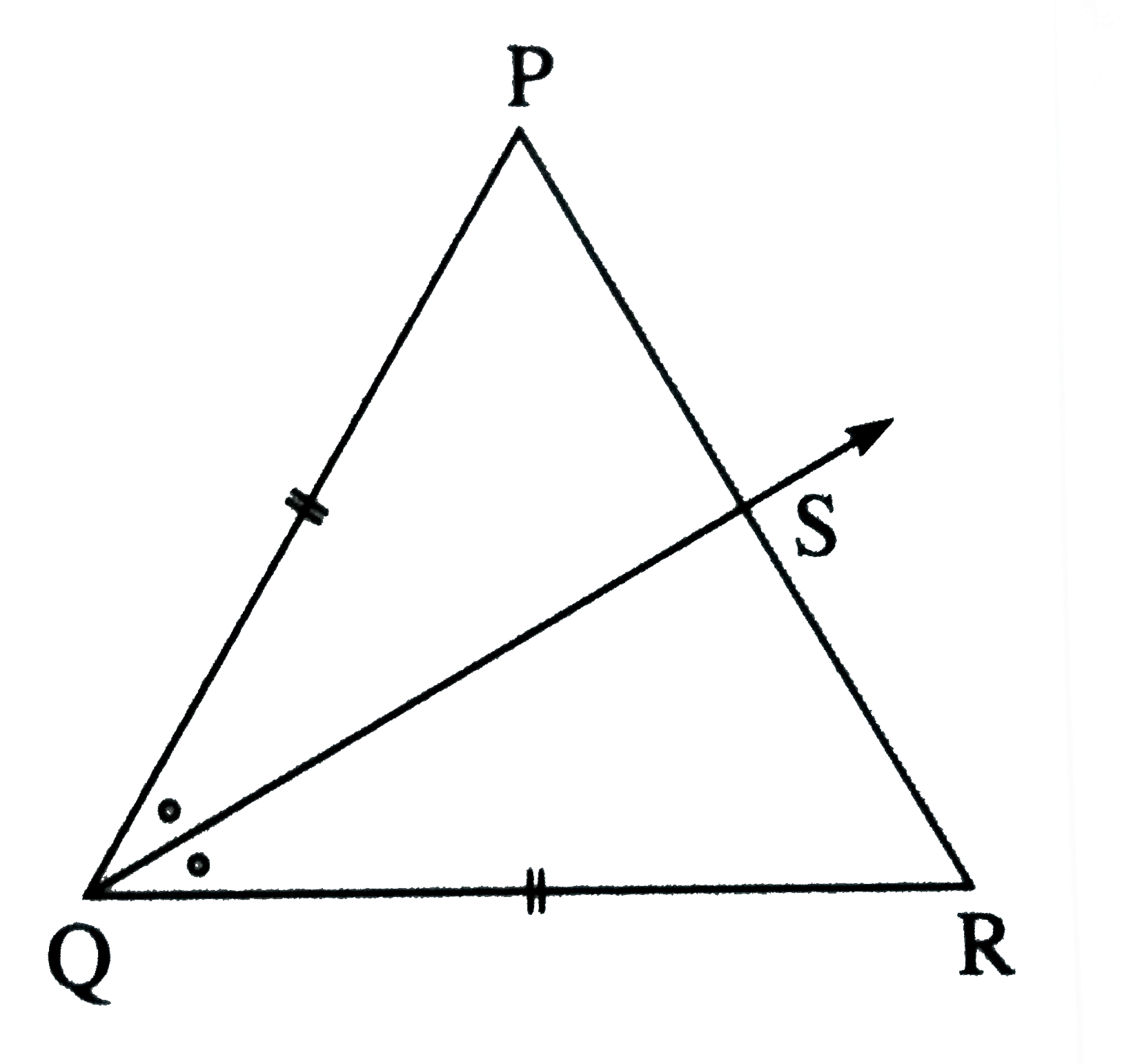
View SolutionIn the figure ray QS is the bisector of ∠PQR and PQ=QR, then PSSR=………..
View Solution