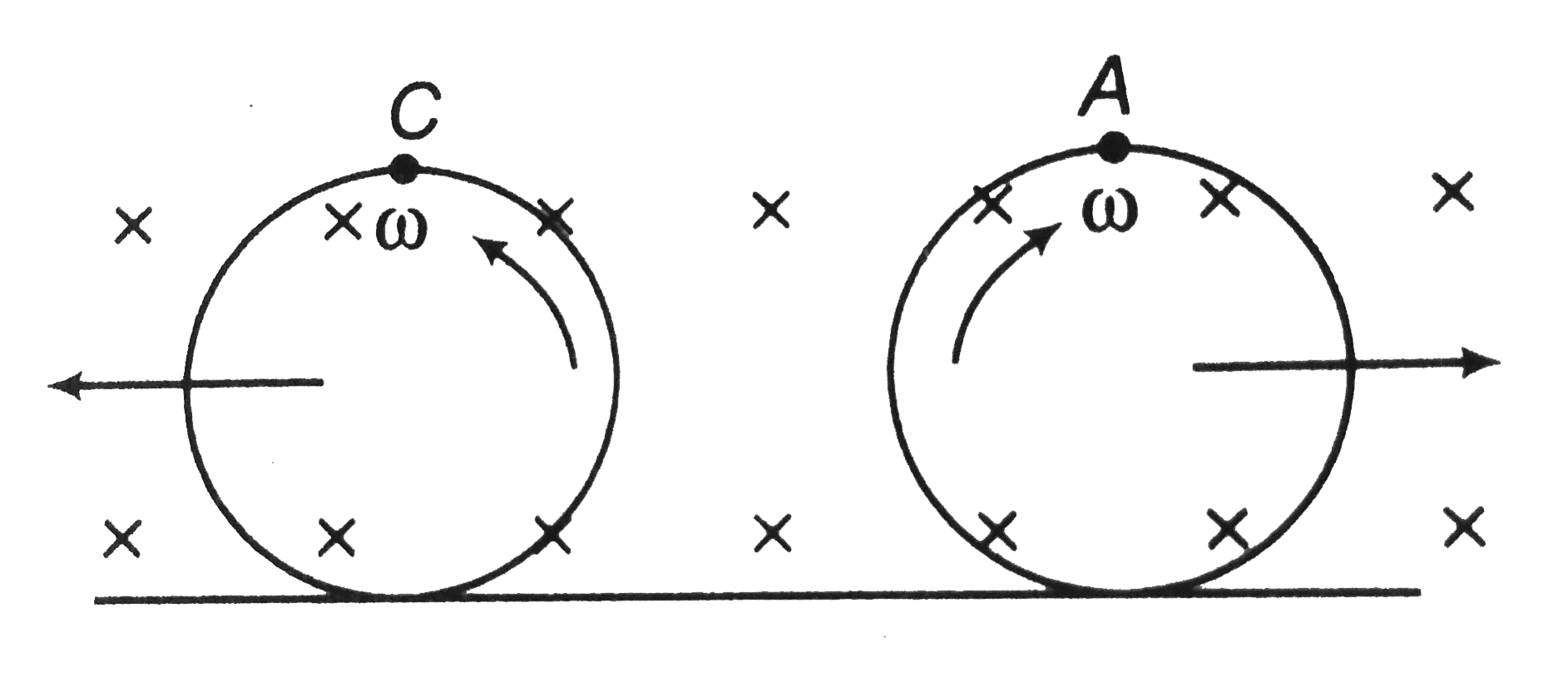
Two metallic rings of radius R are rolling on a metallic rod. A magnetic field of magnitude B is applied in the region. The magnitude of potential difference between points A and C on the two rings (as shown) , will be
0
4BωR2
8BωR2
2BωR2
The correct Answer is:B
VA−V0=Bω(2R)22=2BωR2 ..(i)
V0−VC=Bω(2R)22=2BωR2 ....(ii)
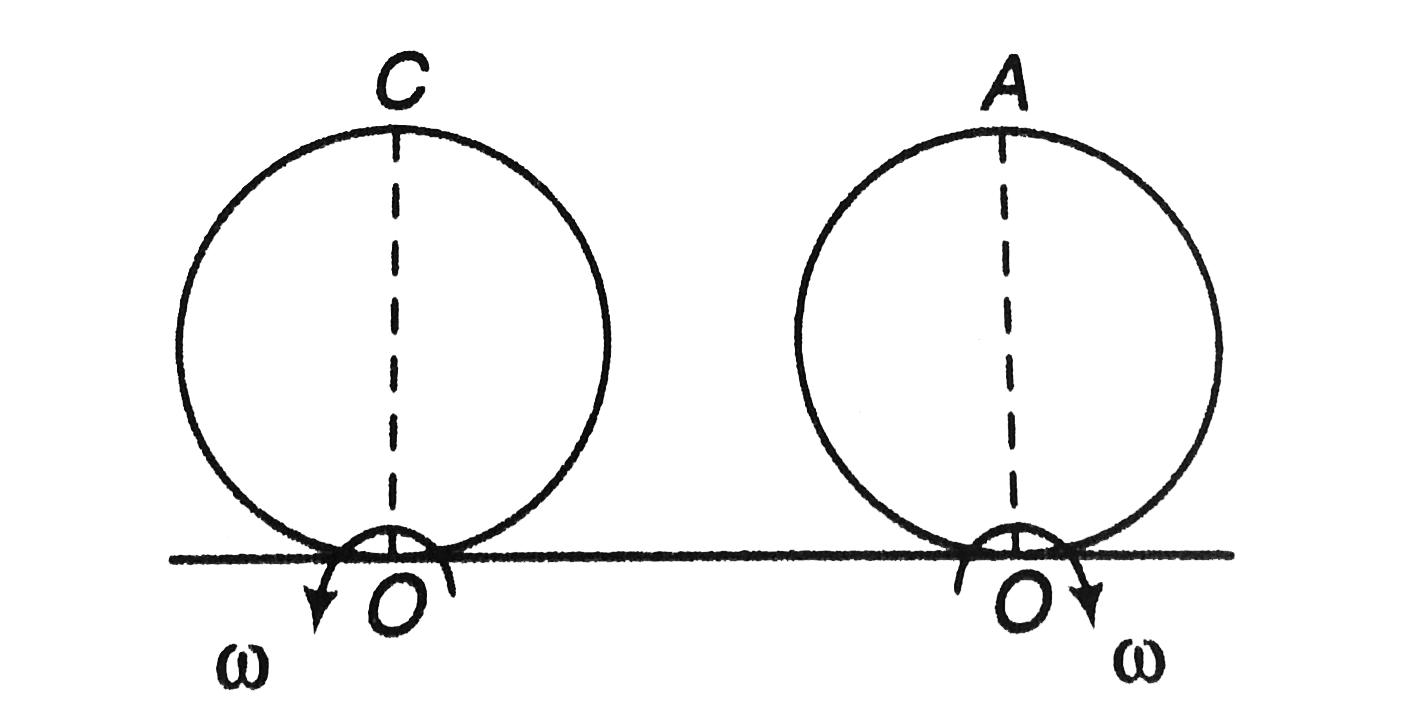
Adding these two equations, we get
VA−Vc=4BωR2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Comprehension Based
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Two conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
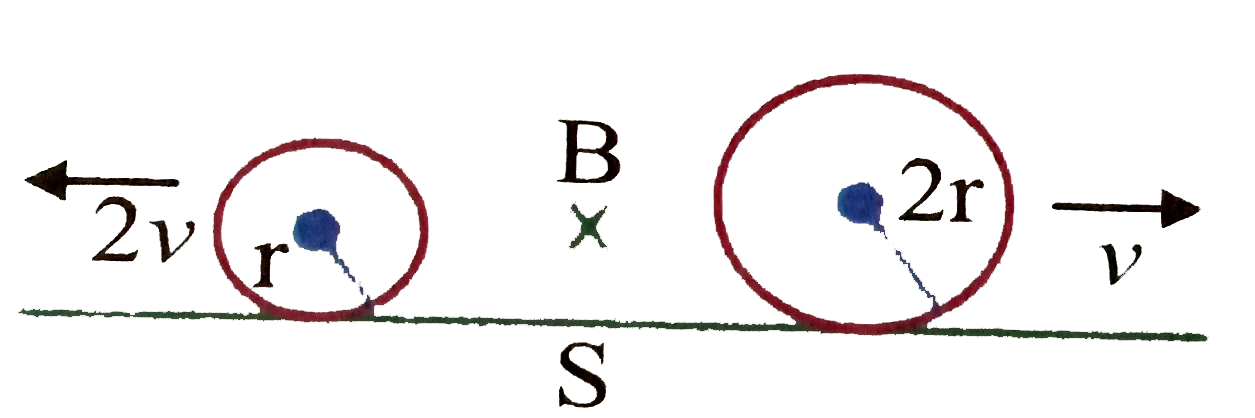
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
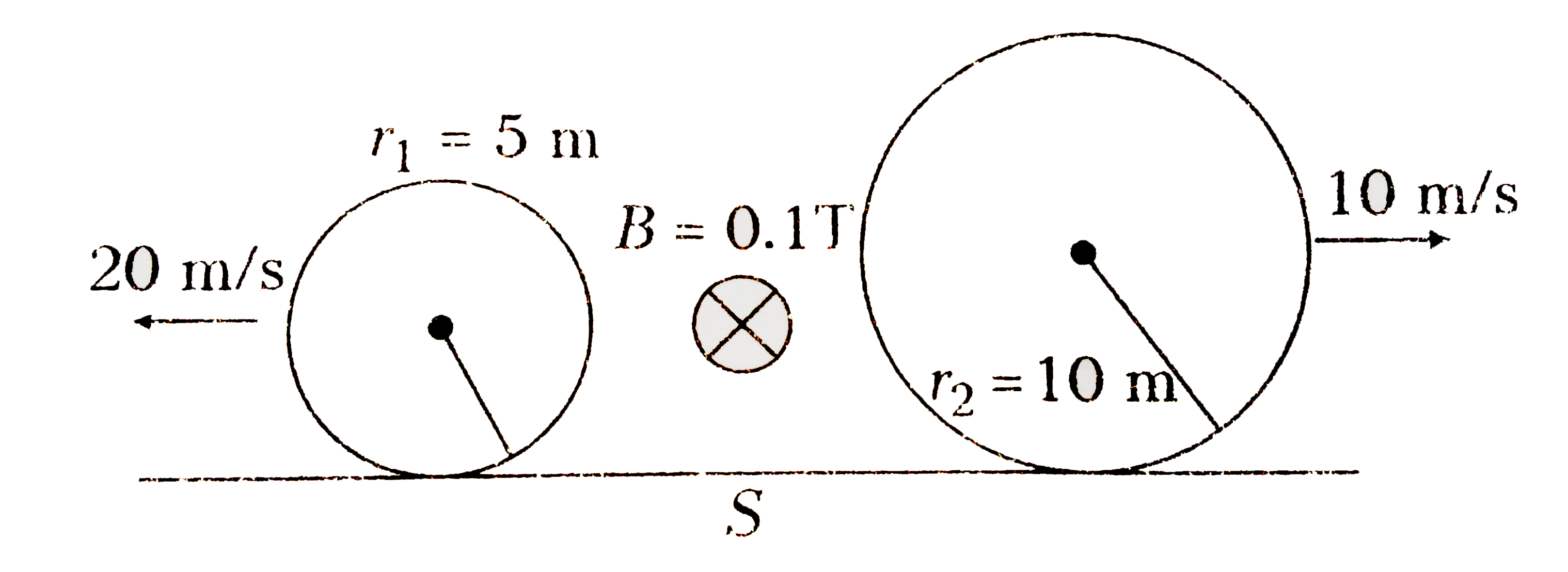
View Solution
Knowledge Check
Two metallic rings of radius R are rolling on a metallic rod. A magnetic field of magnitude B is applied in the region. The magnitude of potential difference between points A and C on the two rings (as shown) , will be
 A0B4BωR2C8BωR2D2BωR2
A0B4BωR2C8BωR2D2BωR2The loop shown moves with a velocity v in a uniform magnetic field of magnitude B, directed into the paper. The potential differene between point P and Q is e. Then
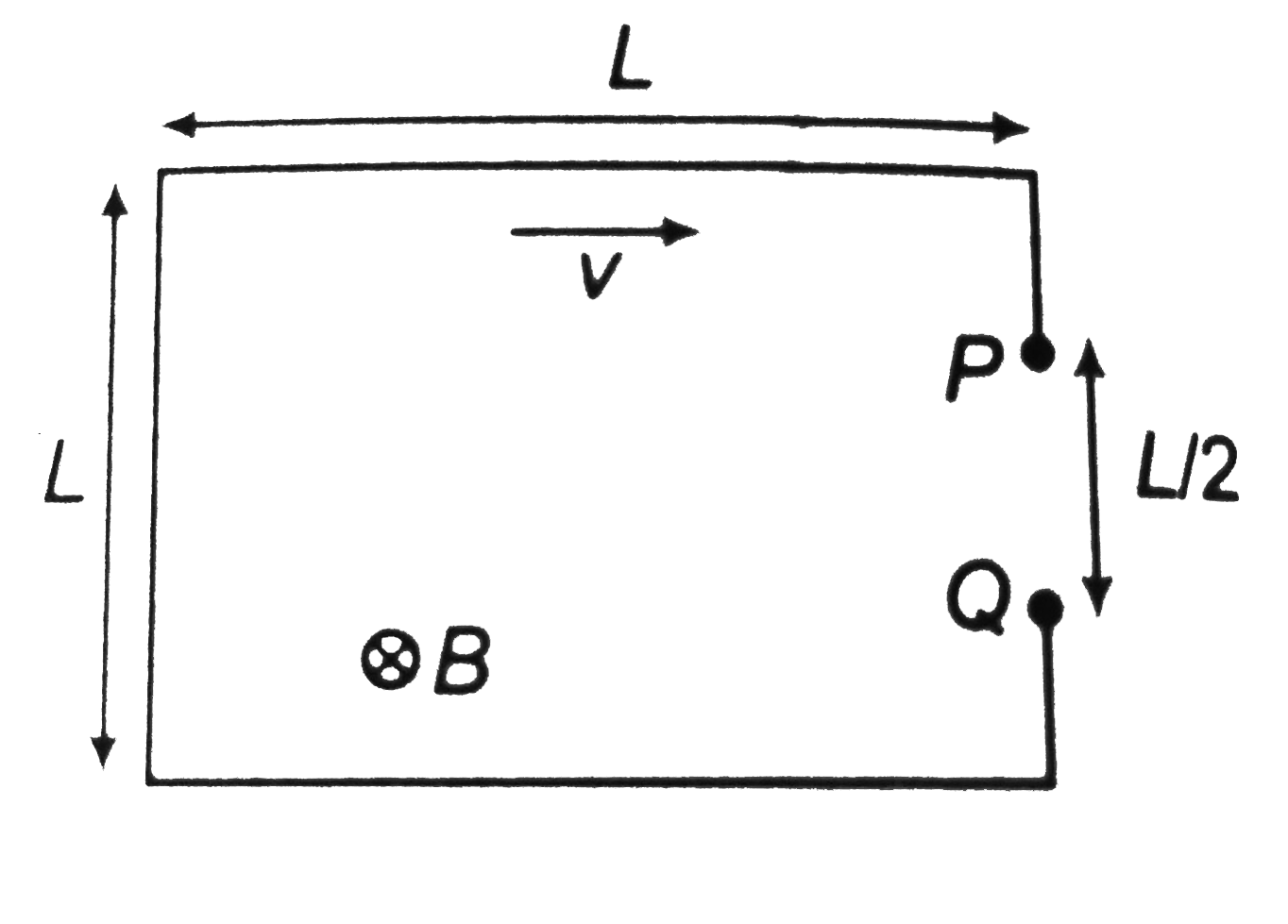 Ae=12BLvBe=BLvCP is positive with respect to QDQ is positive with respect to P
Ae=12BLvBe=BLvCP is positive with respect to QDQ is positive with respect to PTwo conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
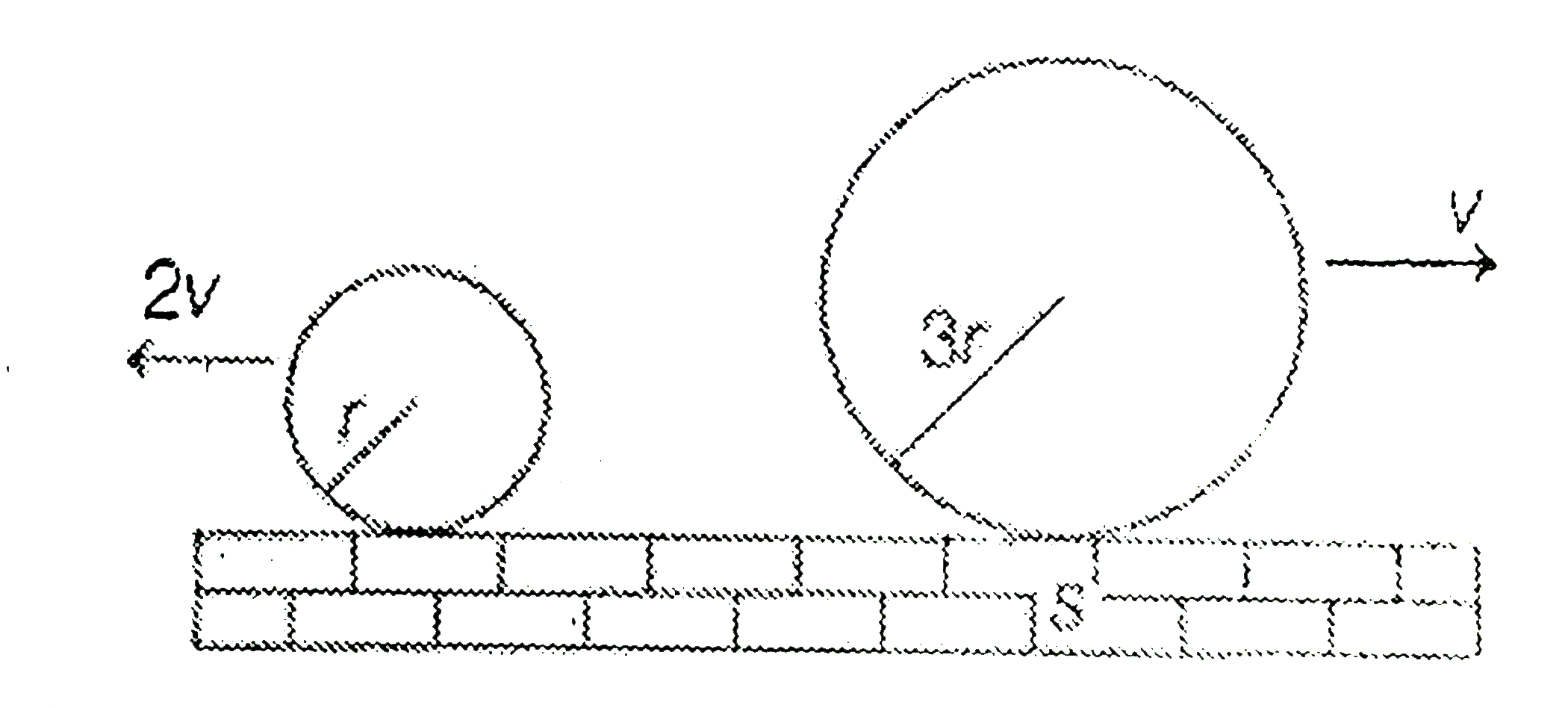 AzeroB2BrvC6BrvD10Brv
AzeroB2BrvC6BrvD10Brv
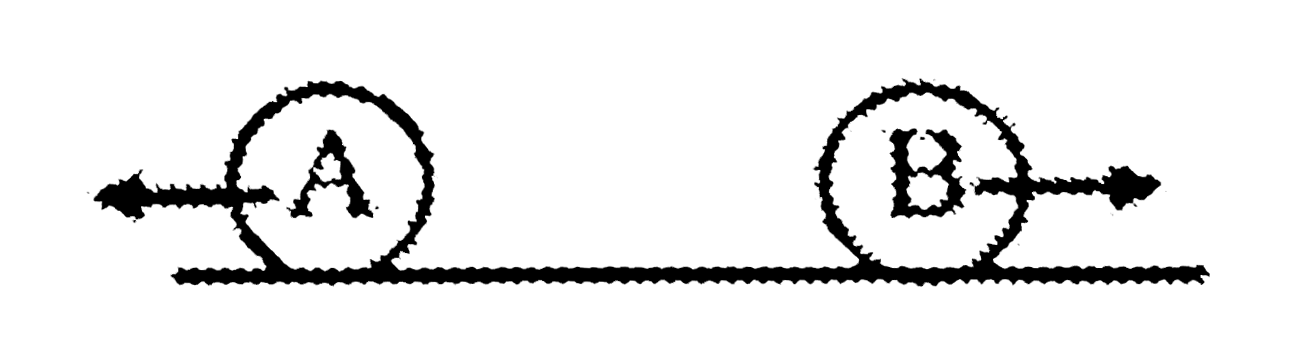
Two identical conducing ring A and B of radius R are in pure rolling over a horizontal conducing plane with same speed (of center of mass) v but in opposite direction. A constant magnetic field B is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is:
View SolutionTwo thin wire rings each having a radius R are placed at a distance d apart with their axes coiciding. The charges on the two rings are +q and −q. The potential difference between the centres of the two rings is
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
View SolutionTwo identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is

View SolutionMetal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
View Solution