In a decaying $L - R$ circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is

A

$(ln 2) \frac{L}{R}$

B

$0.5 \frac{L}{R}$

C

$\sqrt{2} \frac{L}{R}$

D

$(\frac{\sqrt{2}}{\sqrt{2} - 1}) \frac{L}{R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$\frac{1}{2} L i^{2} = = \frac{1}{4} [\frac{1}{4} L i_{0}^{2}]$
So, $i = \frac{i_{0}}{2},$ half value
$∴ t = t_{1 / 2} = (ln 2) τ_{L} = (ln 2) (\frac{L}{R})$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a L-R decay circuit, the initial current at t=0 is I. The total charge that has flown through the resistor till the energy in the inductor has reduced to one-fourth its initial value, is
A $L I / R$
B $L I / 2 R$
C $L i \sqrt{2} / R$
DNone
Question 2 - Select One
LetC be the capacitance of a capacitor discharging through a resistor R. Suppose $t_{1}$ is the time taken for the energy stored in the capacitor to reduce to half its initial value and $t_{2}$ is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio $t_{1} / t_{2}$ will be
A1
B $1 / 2$
C $1 / 4$
D2
Question 3 - Select One
The capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :

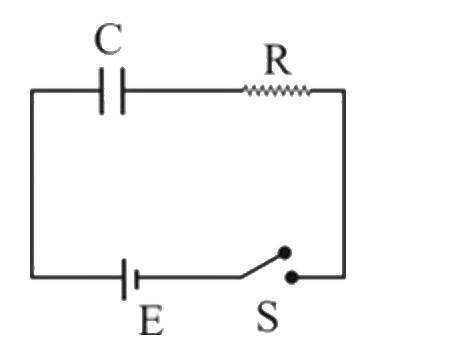ARC
BRC ln 2
CRC ln 4
D2RC

DC PANDEY-ELECTROMAGNETIC INDUCTION-Level 2 Single Correct

Home
Ask Doubt
Profile