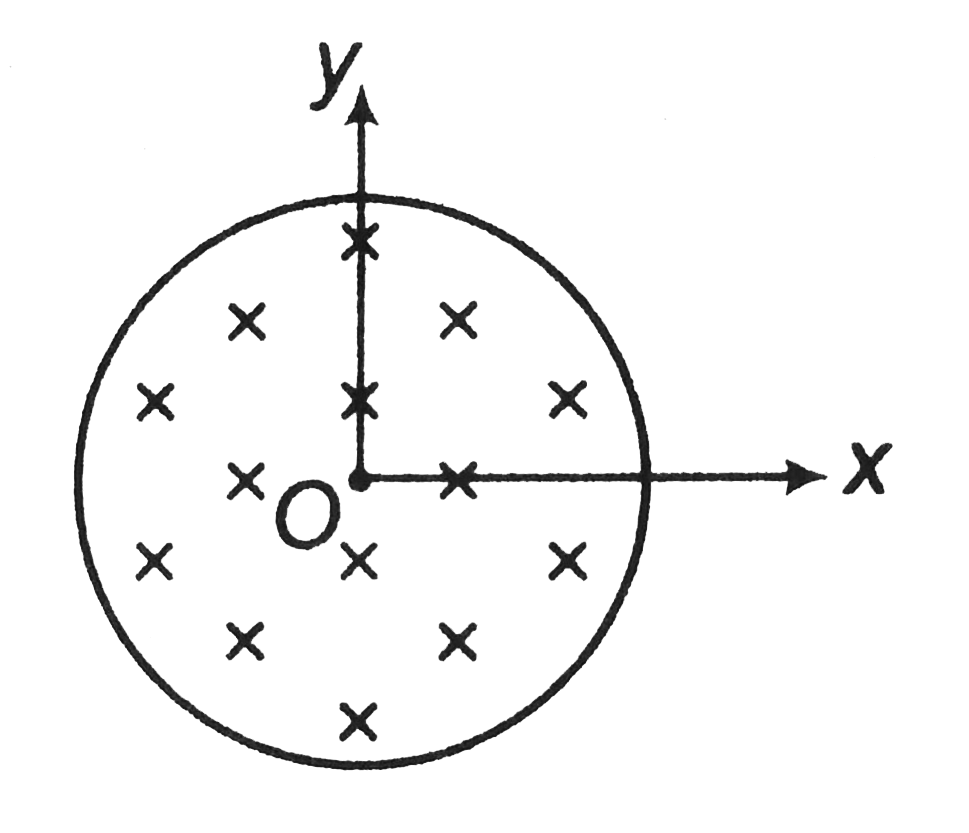
A uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5 cm as shown in figure.

The force on an electron at P at t=2.0 s is
96×10−21N
48x10−21N
24×10−21N
zero
The correct Answer is:B
dBdt=(6t2+24)T/s
At t=2s,dBdt=48T/s
El=dϕdt=S(dBdt)
or E(2πr)=πr2(dBdt)
∴E=r2.dBdt ...(i)
F=qE=qr2dBdt
=(1.6×10−19)(1.25×10−2)2(48)
=48×10−21N
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Subjective
20 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A massless non conducting rod AB of length 2l is placed in uniform time varying magnetic field confined in a cylindrical region of radius (R>l) as shown in the figure. The center of the rod coincides with the centre of the cylin- drical region. The rod can freely rotate in the plane of the Figure about an axis coinciding with the axis of the cylinder. Two particles, each of mass m and charge q are attached to the ends A and B of the rod. The time varying magnetic field in this cylindrical region is given by B=B0[1−t2] where B0 is a constant. The field is switched on at time t=0. Consider B0=100T,l=4cmqm=4π100C/kg. Calculate the time in which the rod will reach position CD shown in the figure for th first time. Will end A be at C or D at this instant ?
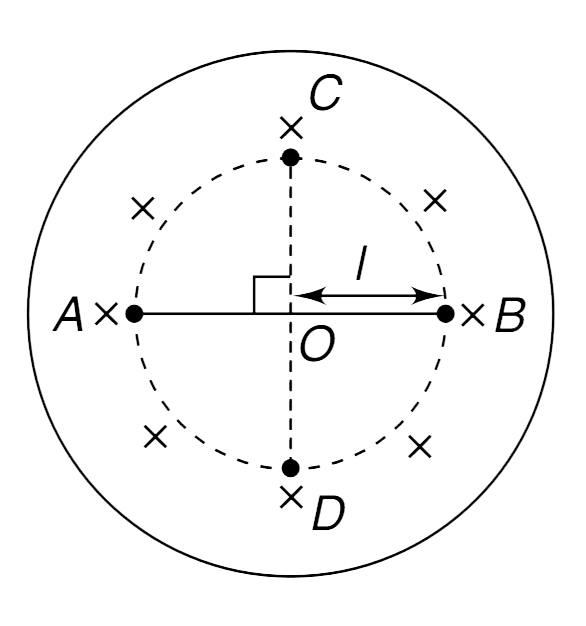
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
View Solution
Knowledge Check
A uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem isA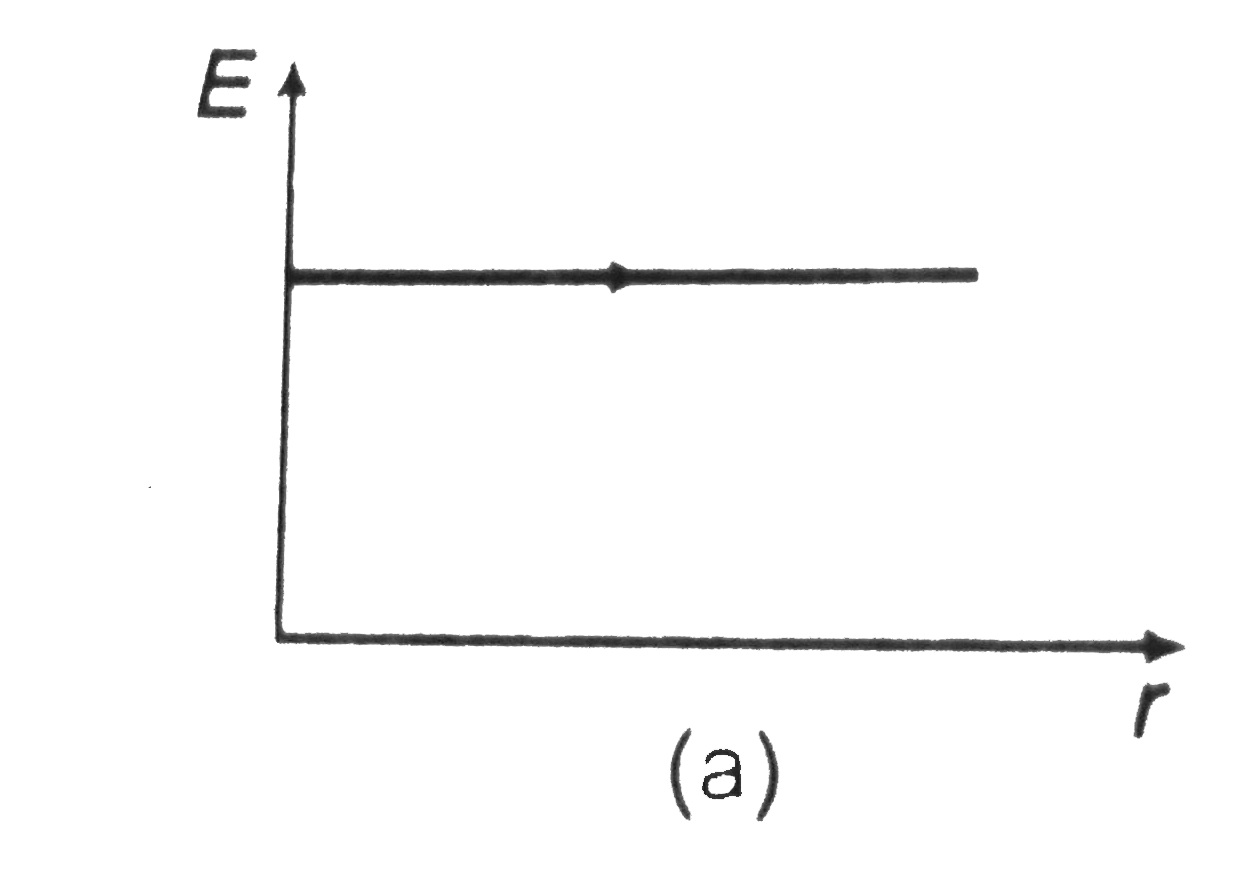 B
B C
C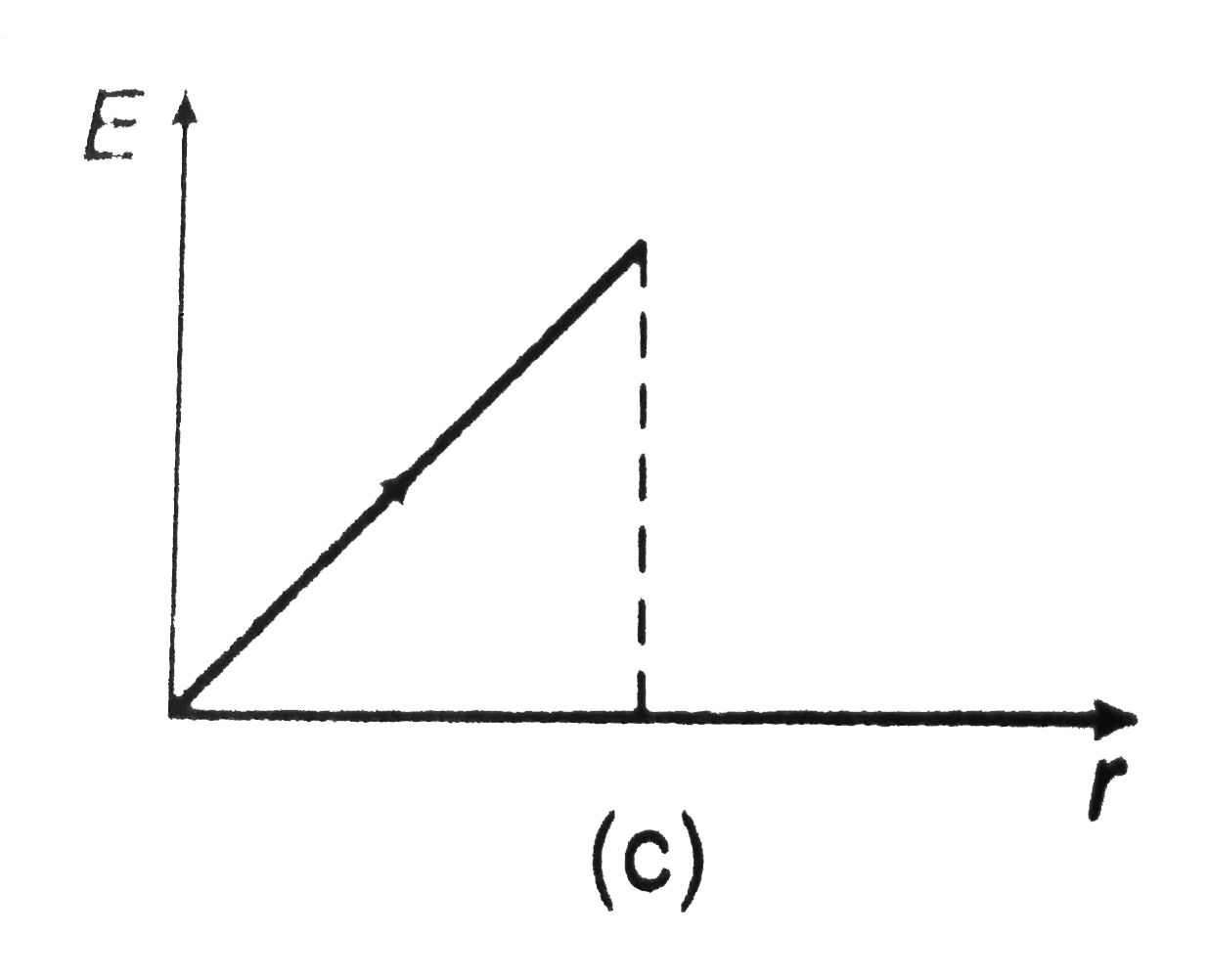 D
D
A uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

In the previous problem, the direction of circular electric lines at t=1s isAclockwiseBanti clociwiseCno current is inducedDcannot be predictedA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
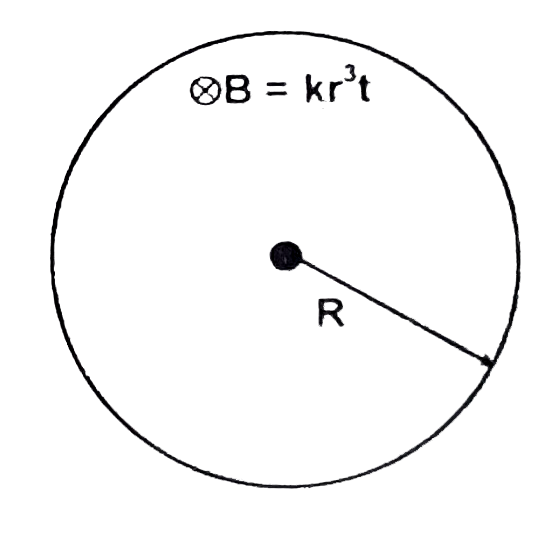 AKR420BKR440CKR460DKR480
AKR420BKR440CKR460DKR480
A time varying magnetic field is present in a cylindrical region of radius R as shown in figure ( cross - sectional view ). B is increasing with time, mark out the correct statement (s) for the given situation, r being the distance from centre of cylindrical region.

View SolutionA uniform but time varying magnetic field exists in a cylindrical region as shown in the figure. The direction of magnetic field is into the plane of the paper and its magnitude is decreasing at a constant rate of 2×10−3T/s. A particle of charge 1μC is moved slowly along circle of radius 1m by an external force as shown in figure. The plane of the circle of radius 1m by an external force as shown in figure. The plane of he circle lies in the plane of the paper and it is concentric with the cylindrical region. The work done by the external force in moving this charge along the circle will be

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.

View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View Solution
