Metal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
Electric field at any point on the ring is zero.
Electric field at any point on the ring is α(R)/(2)
Emf induced in the ring is zero
Emf induced in the ring is πaR2
The correct Answer is:B, D
To solve the problem, we need to determine the induced electromotive force (EMF) and the electric field at any point on the metal ring when the magnetic field is changing at a rate of α.
1. Understanding the Problem:
- We have a metal ring of radius R placed perpendicular to a uniform magnetic field B.
- The magnetic field B is changing at a rate α, which can be mathematically represented as dBdt=α.
2. Calculating Magnetic Flux:
- The magnetic flux Φ through the ring is given by the formula:
Φ=B⋅A
where A is the area of the ring. Since the ring is perpendicular to the magnetic field, we can simplify this to:
Φ=B⋅πR2
Here, πR2 is the area of the circle formed by the ring.
3. Finding the Induced EMF:
- According to Faraday's law of electromagnetic induction, the induced EMF (E) is given by the negative rate of change of magnetic flux:
E=−dΦdt
- Since Φ=B⋅πR2, we differentiate it with respect to time:
dΦdt=πR2dBdt
- Substituting dBdt=α:
dΦdt=πR2α
- Thus, the induced EMF is:
E=−πR2α
4. Calculating the Electric Field:
- The induced EMF is also related to the electric field E around the ring and the circumference of the ring:
E=E⋅L
where L is the circumference of the ring, given by L=2πR.
- Therefore, we can express the electric field as:
E=EL=−πR2α2πR
- Simplifying this gives:
E=−Rα2
5. Final Results:
- The induced EMF is:
E=πR2α
- The electric field at any point on the ring is:
E=Rα2
Summary of Answers:
- Induced EMF: E=πR2α
- Electric Field: E=Rα2
- We have a metal ring of radius R placed perpendicular to a uniform magnetic field B.
- The magnetic field B is changing at a rate α, which can be mathematically represented as dBdt=α.
- The magnetic flux Φ through the ring is given by the formula:
Φ=B⋅A
where A is the area of the ring. Since the ring is perpendicular to the magnetic field, we can simplify this to:
Φ=B⋅πR2
Here, πR2 is the area of the circle formed by the ring.
- According to Faraday's law of electromagnetic induction, the induced EMF (E) is given by the negative rate of change of magnetic flux:
E=−dΦdt
- Since Φ=B⋅πR2, we differentiate it with respect to time:
dΦdt=πR2dBdt
- Substituting dBdt=α:
dΦdt=πR2α
- Thus, the induced EMF is:
E=−πR2α
- The induced EMF is also related to the electric field E around the ring and the circumference of the ring:
E=E⋅L
where L is the circumference of the ring, given by L=2πR.
- Therefore, we can express the electric field as:
E=EL=−πR2α2πR
- Simplifying this gives:
E=−Rα2
- The induced EMF is:
E=πR2α
- The electric field at any point on the ring is:
E=Rα2
- Induced EMF: E=πR2α
- Electric Field: E=Rα2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS BASED ON GIVEN PASSAGE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (AIPMT/NEET & Other State Boards for Medical Entrance)
8 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Knowledge Check
A circular loop of metal wire of radius r is placed perpendicular to uniform magnetic field B. Half of the loop is folded about the diameter with constant angular velocity ω. If resistance of the loop is R then current in the loop is
Azero, when θ=0Bπr2Bω2R when θ=0Cπr2Bω2R when θ=π6Dπr2Bω4R when θ=π6A circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of ω, about its own axis , then the induced emf in the coil is __
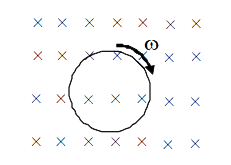 ABAω2πBB(2πr)ωC0Dnone of the above
ABAω2πBB(2πr)ωC0Dnone of the aboveA magnet is placed in a non-uniform magnetic field. It experiences
Aa force but not a torqueBa torque but not a forceCa force and a torqueDneither a force nor a torque
Path of an electron entering perpendicular in a uniform magnetic field will be:
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA semi circular conducting ring acb of radius R moves with constant speed v in a plane perpendicular to uniform magnetic field B as shown in figure.
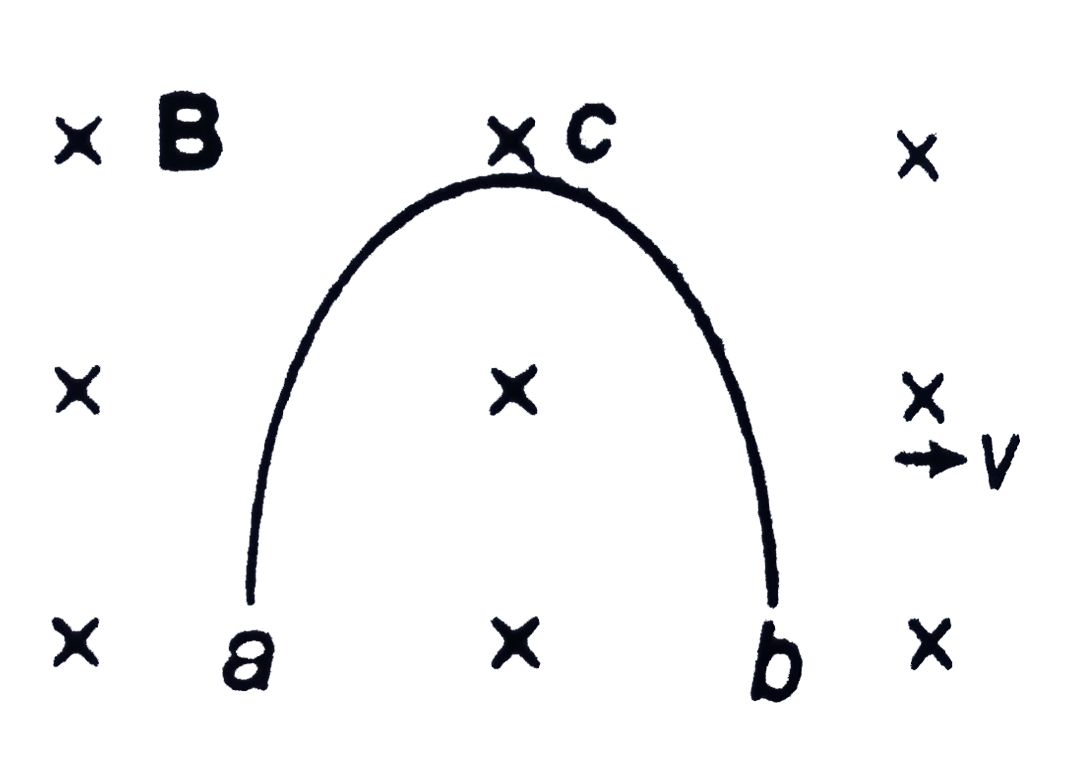
Identify the correct statement.
View Solution
