A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
A

B
C
D
Video Solution
Text Solution
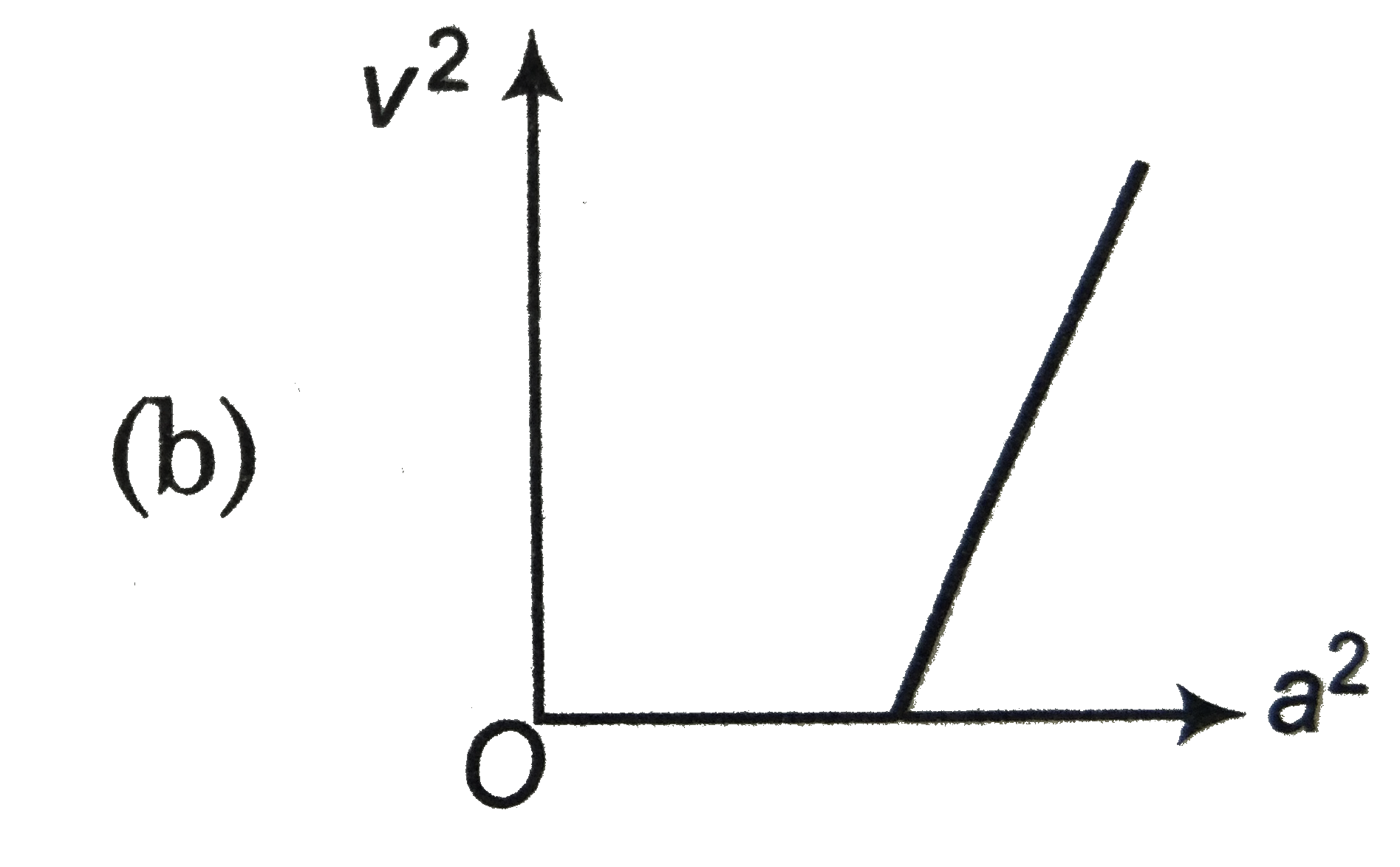
The correct Answer is:C
If v=v0sinωt, then
a=dvdt=v0ωcosωt
sinωt=vv0 …(i)
cosωt=av0ω …(ii)
Squaring and adding these equations, we get
1=v2v20+a2v0ω
∴v2=(−v0ω)a2+v20
Hence, v2 versus a2 equation is a straight line with positive intercept and negative slope.
|
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Knowledge Check
A particle is performing a linear simple harmonic motion if the acceleration and the corresponding velocity of the particle are a and v respectively. Which of the following graph is correct?
A B
B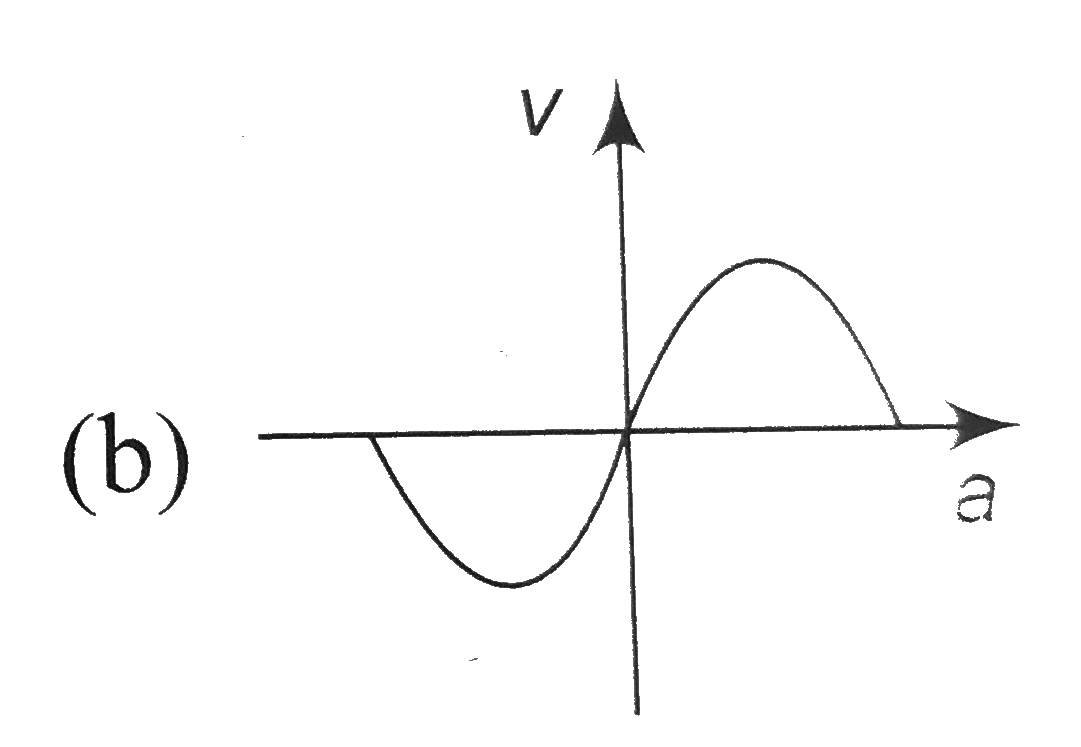 C
C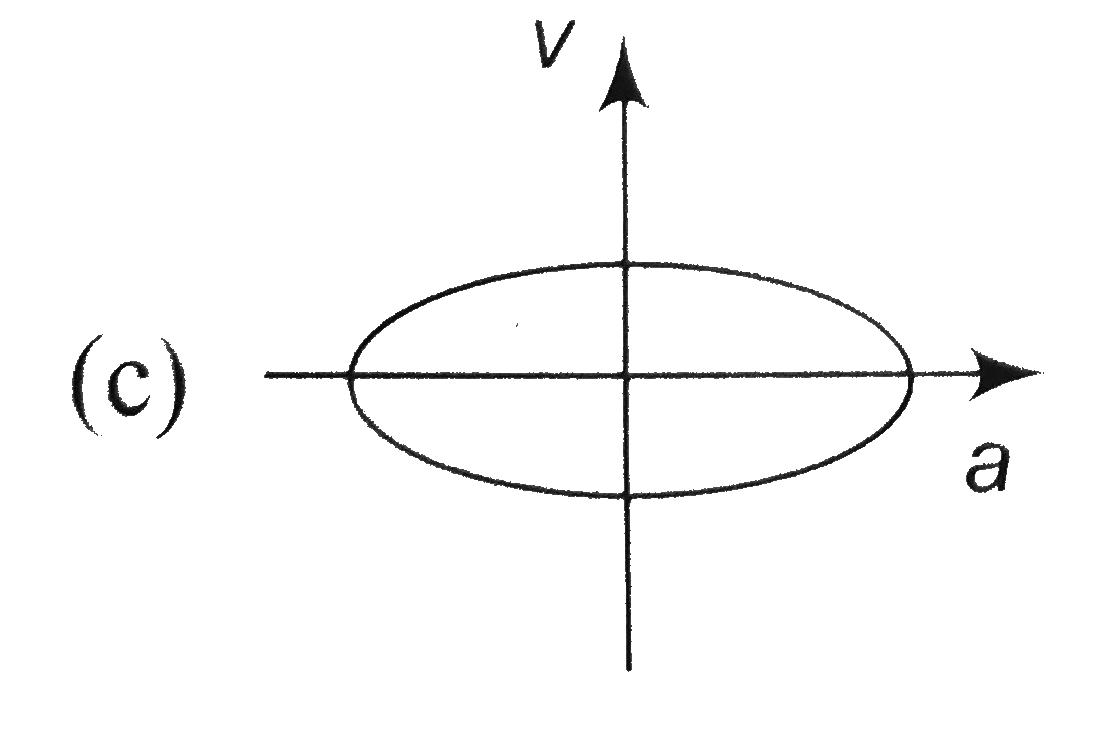 D
D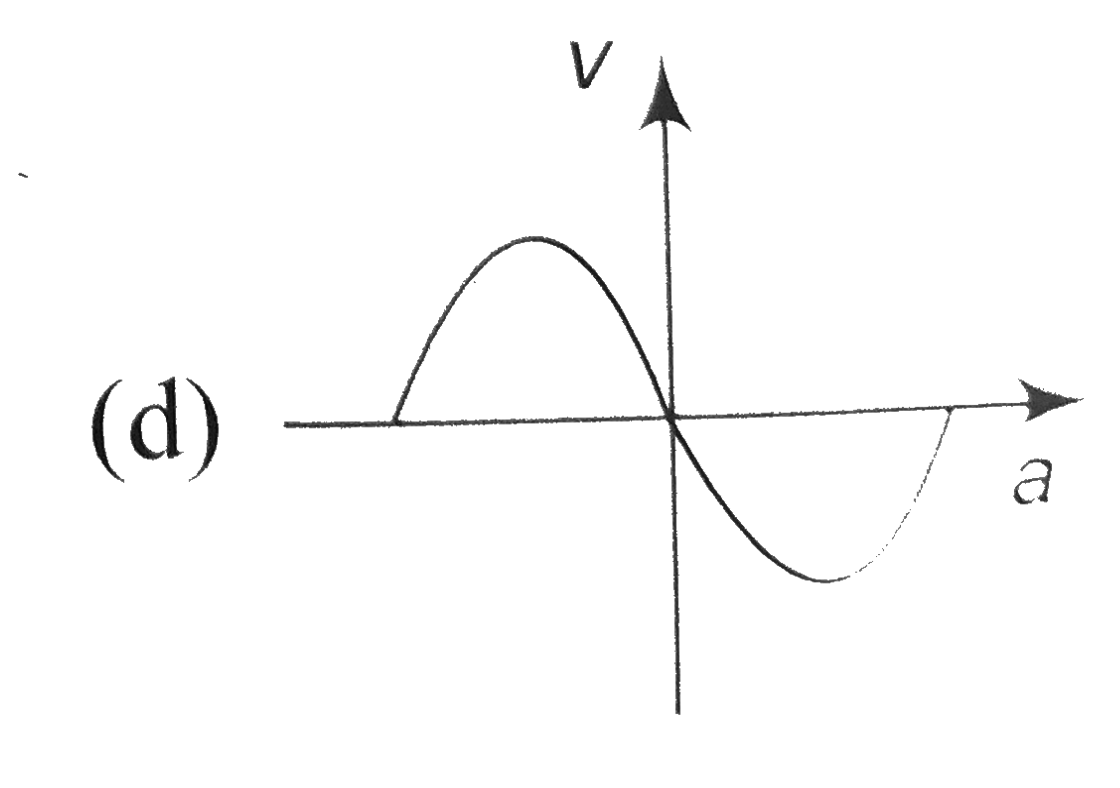
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.Dits linear velocity and acceleration always attain their peak values simlataneaously.A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
A B
B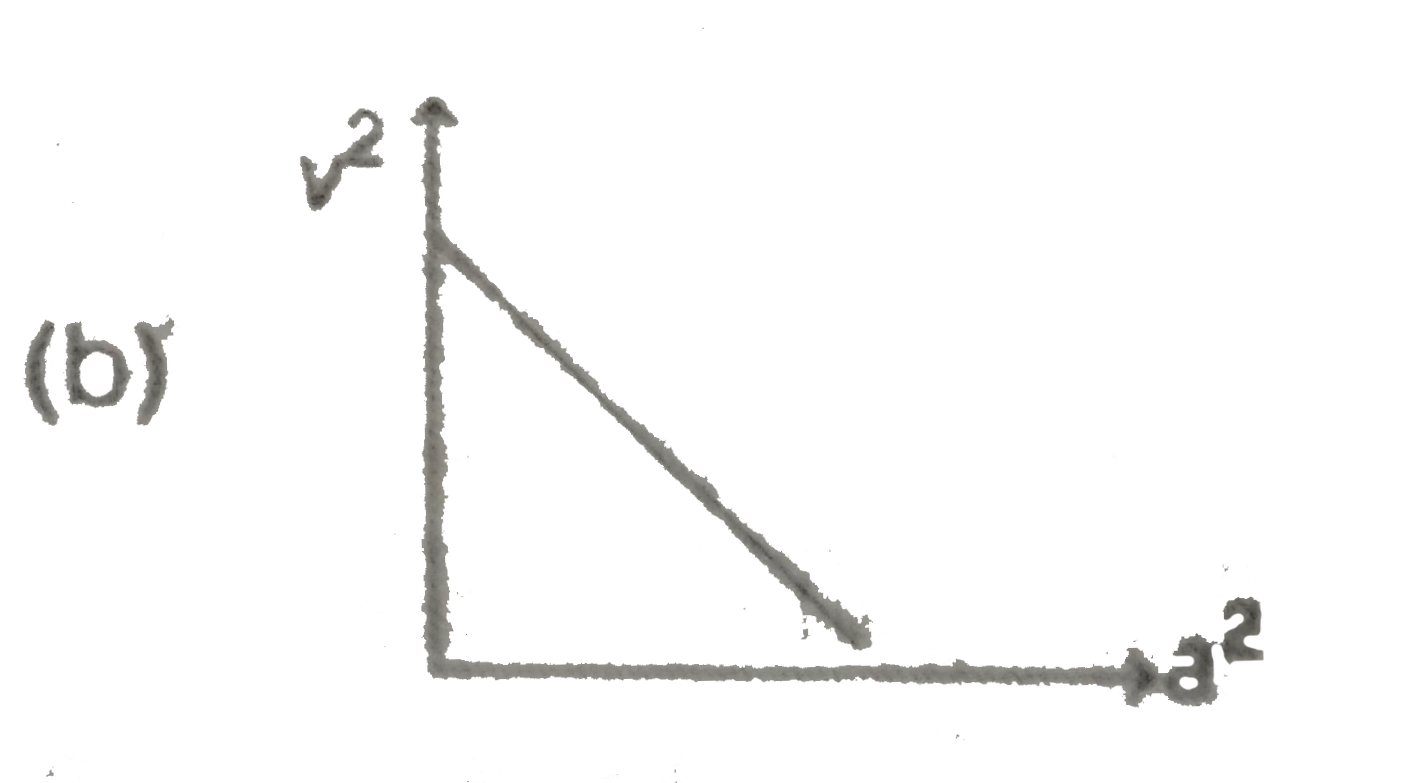 C
C D
D
If a particle is executing simple harmonic motion, then acceleration of particle
View SolutionA particle is performing linear S.H.M. If the acceleration and corresponding velocity of the particle are ∝ and v respectively and if we plot v2 on Y axis and ∝2 on X axis, then the graph will be
View SolutionA particle is executing a simple harmonic motion its maximum acceleration is a and maximum velocity is β .Then its time of vibration will be
View SolutionLet v and a represent instantaneous velocity and acceleration of a particle respectively.
View SolutionA particle is performing simple harmonic motion with amplitude A and angular velocity ω . The ratio of maximum velocity to maximum acceleration is
View Solution


