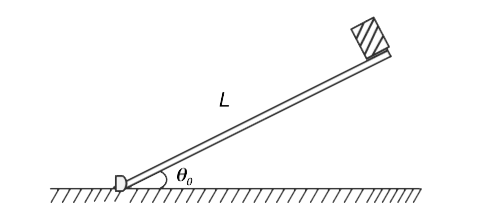
A uniform stick of length L and mass M hinged at end is released from rest at an angle θ0 with the vertical show that when the angle with the vertical is θ. The hinge exerts of force Fr along the stick and Ft perpendicular tot he stick given by Fr=12Mg(5cosθ−3cosθ0) and Ft=14Mgsinθ

(i) C is the centre of mass of the rod. Let ω be the angular speed of rod about point O at angle θ. From conservation of mechanical energy.
Mg(L)2(cosθ−cosθ0)=12(ML23)ω2
∴ω2=3gL(cosθ−cosθ0) ..(i)
Now, Fr−Mgcosθ=M(L2)ω2 ..(ii)
From eqs. (i) and (ii) we get
Fr=12Mg(5cosθ−3cosθ0) hence proved
(ii) angular acceleration of rod at this instant
α=τI=Mg(L)2sinθML23
=32gsinθL
Tangential acceleration of COM.
at=(α)(L2)=34gsinθ ...(iii)
Now Ft+Mgsinθ=Mat ....(iv)
from eqs. (iii) and (iv), we get
Ft=−14Mgsinθ
Here negative sign implies that direction of Ft is opposite to the component Mgsinθ.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform stick of length L is pivoted at one end on a horizontal table. The stick is held forming an angle θ0 with the table. A small block of mass m is placed at the other end of the stick and it remains at rest. The system is released from rest
(a) Prove that the stick will hit the table before the block if cosθ0≥√23
(b) Find the contact force between the block and the stick immediately before the system is released.Take θ0=cos−1(√23)
(c) Find the contact force between the block and the stick immediately after the system is released if θ0cos−1(√23).
View SolutionA uniform rod of length 2a is held with one end resting on a smooth horizontal table making an angle a with the vertical. Show that when the rod is released, its angular velocity when it makes an angle θ with the vertical is given by
ω=[6g(cosα−cosθ)(1+3sin2α)]
View Solution
Knowledge Check
A uniform stick of mass M is placed in a frictionless well as shown. The stick makes an angle θ with the horizontal. Then the force which the vertical wall exerts on right end of stick is :
 AMg2cotθBMg2tanθCMg2cosθDMg2sinθ
AMg2cotθBMg2tanθCMg2cosθDMg2sinθOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mgOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mg
A rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
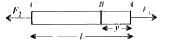
The tension in the rod at a distance y from the end A is given by
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View SolutionA uniform wooden stick of mass 1.6 kg and length l rests in an inclined mannar on a smooth, vertical wall of height h(<l) such that a small portion of the stick extends beyond the wall. The reaction force of th wall on the stick is perpendicular to the stick. The stick makes an angle of 30∘ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/l and the friectional force f at the bottom of the stick are (g=10ms2)
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
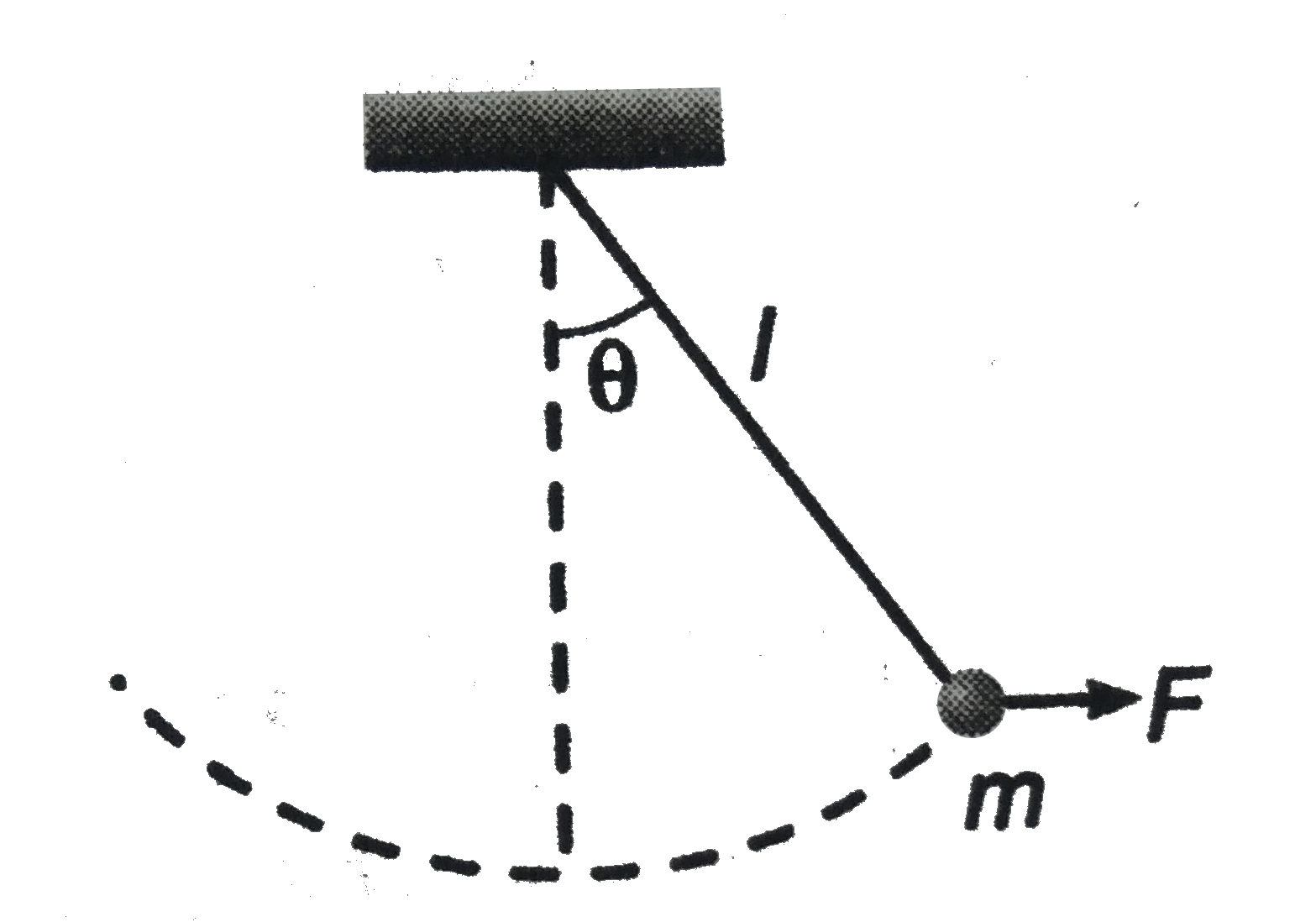 .
.
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View Solution