A uniform rod AB of mass 3m and length 4l, which is free to turn in a vartical plane about a smooth horizontal axis through A, is released from rest when horizontal When the rod first impulse exerted by the peg on the rod it.
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.

(a). From conservation of mechanical energy
(3m)(g)(2l)=12Iω2
=12[(3m)(4l)23]ω2=8ml2ω2
∴ω=(12√3gl)
∴J=83ml√3gl
or J=83m√3gl
(b). let ω' be the angular speed in opposite direction again applying conservation mechanical energy
(3m)(g)(l)=12I(ω')2=8ml2(ω')2
∴ω'=12√2√3gl
Now, applying angular impulse = change in angular momentum
∴J(3l)=l(ω+ω')=(16ml2)12√3gl(1+1√2
∴J=43m√6gl(√2+1)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
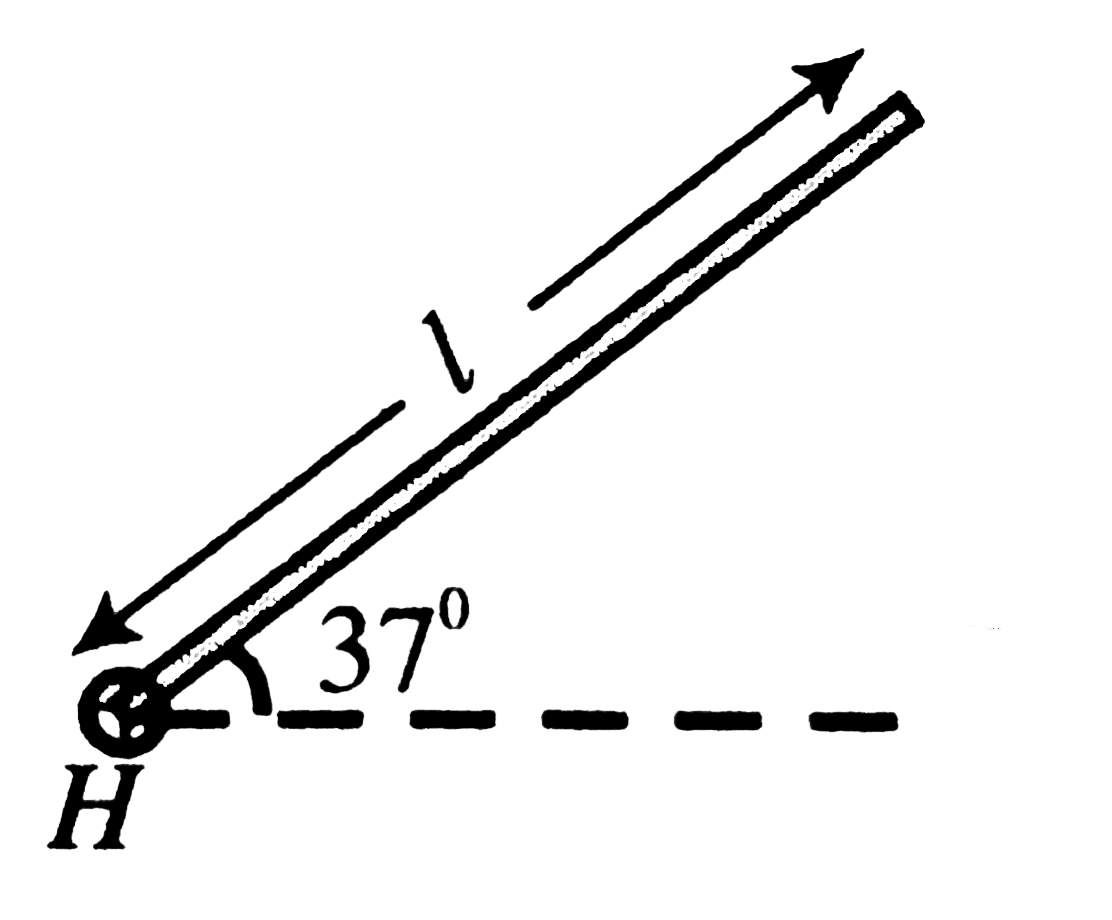
View Solution
Knowledge Check

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθA slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is
 A√104 mg along horizontalBmg along verticalC√104mg alonng a line making an angle of tan−1(13) with the horizontalD√104mg along a line making an angle of tan−1(3) with the horizontal
A√104 mg along horizontalBmg along verticalC√104mg alonng a line making an angle of tan−1(13) with the horizontalD√104mg along a line making an angle of tan−1(3) with the horizontalA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2gl
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
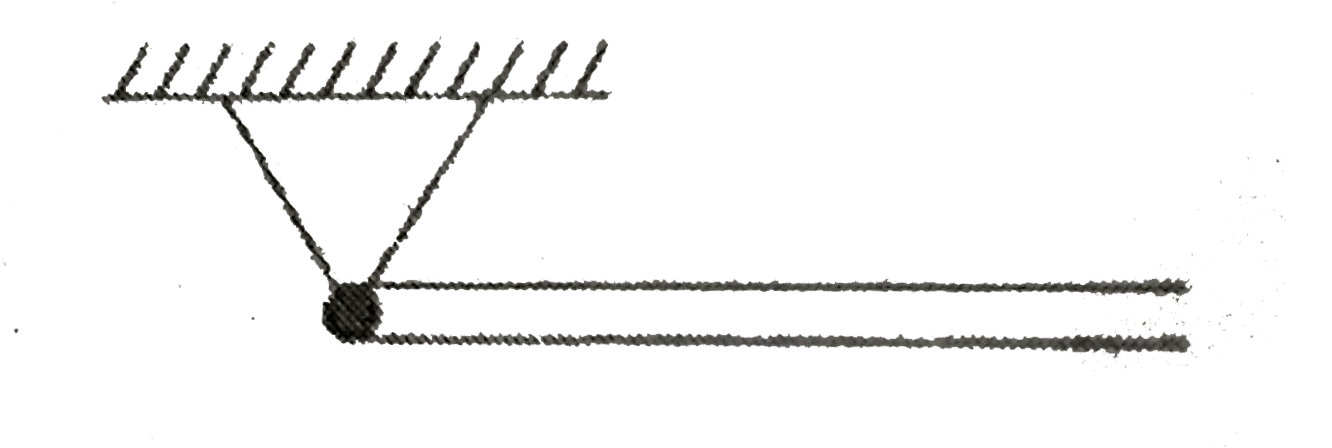
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
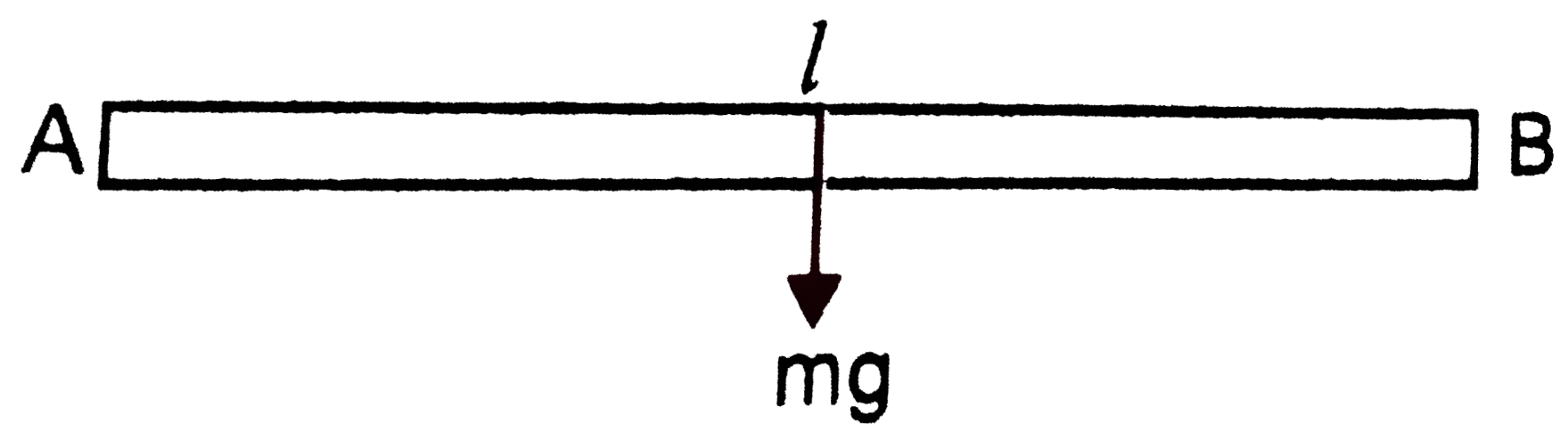
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.
The point about which rod rotates just after impulse being applied is located at
View Solution