
A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
Equation of motion are,
F+f1=Ma1 ..(i)
f1+f2=Ma2 ..(ii)
2F−f2=2Ma3
α=(f1−f2)R12MR2
or α=2(f1−f2)MR ..(iv)
for no slipping condition,
a2+Rα=a1 .(v)
and a2−Rα=a3 .(vi)

we have six unknowns, f1,f2,a1,a2,a3 and α
Solving the above six equations we get
a1=21F26M and a2=F26M
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
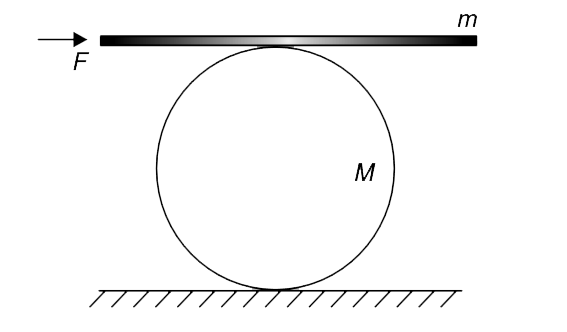
View SolutionA plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View Solution
Knowledge Check
The acceleration a of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping take place between cylinder and plank)
 Ag2sinθB2gsinθCgsinθDgtanθ
Ag2sinθB2gsinθCgsinθDgtanθThe acceleration α of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping takes place between cylinder and plank)
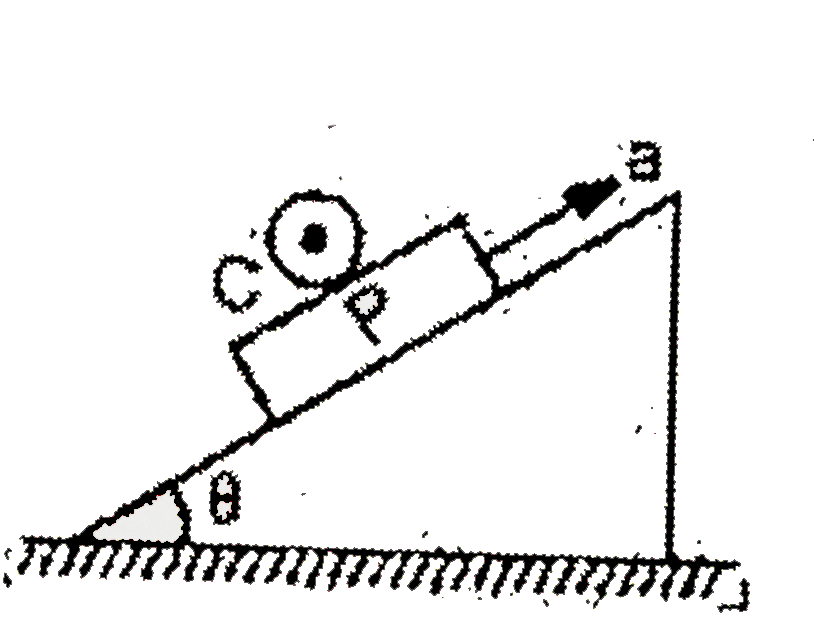 Ag2sinθB2gsinθCgsinθD√2gsinθ
Ag2sinθB2gsinθCgsinθD√2gsinθA uniform sphere of mass m is positioned between two horizontal planks A and B of mass 2m and m respectively as shown. Ground surface is smooth and friction between planks and sphere is sufficient so that no slipping takes place. Horizontal forces F1 and F2 are applied on plank so that acceleration of sphere is zero. Plank B is moving toward right with acceleration a. Which of the following is/are correct ?
 ABoth planks have same accelerationBNet force sphere is non-zeroCF1+F2=175maDf=5ma
ABoth planks have same accelerationBNet force sphere is non-zeroCF1+F2=175maDf=5ma
A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
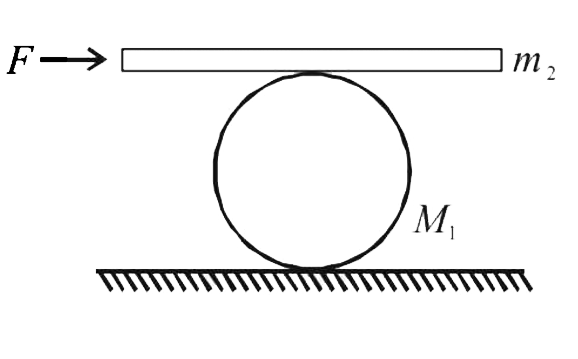
(b) the magnitudes and direction of frictional force at contact points.
View SolutionA cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.

View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank

View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.
View SolutionA sphere of radius 1 m is kept on a plank kept on horizontal surface. Accelerations of plank and centre of sphere are indicated in the figure.

If sphere is not slipping on the plank then its angular acceleration is
View Solution

