A circular tube of mass M placed veticlly on a horizontal surface as shown in the figure. Two small spheres, each of mass m , just fit in the tube, are released from the top. If θ gives the angle between radius vector of eirther ball with the vertical, obtain the value of the ratio M/m if the tube breacks its contact with ground when θ=60∘ . Neglect any friction.

Speed of each particle at angle θ is,
v=√2gh , (from energy conservation)
where, h=R(1−cosθ)
:. v=√2gR(1−cosθ)
N+mgcosθ=mv2R
or N+mgcosθ=2mg(1−cosθ)
or N=2mg−3mgcosθ ...(i)
The tube breaks its contact with ground when Substituting, 2Ncosθ=Mg
or 4mgcosθ−6mgcos2θ=Mg
Substituting θ=60∘
2mg−3mg2=Mg
or Mm=12
Intially bnormal reaction on each vball will be radially outward and later it will be radailly inward, so that normal reactions on tube is radially outward to break it off from the groung .
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
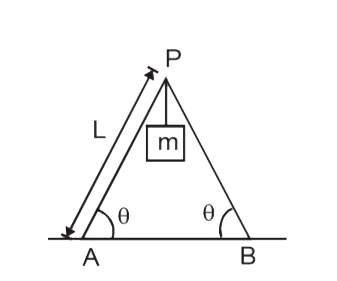
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View Solution
Knowledge Check
Cube of mass m kept on rough horizontal surface. Two insects each mass m. Moving in the cube with equal acceleration. a0 from D to E and H to F what is the frictional force by ground on the tube.
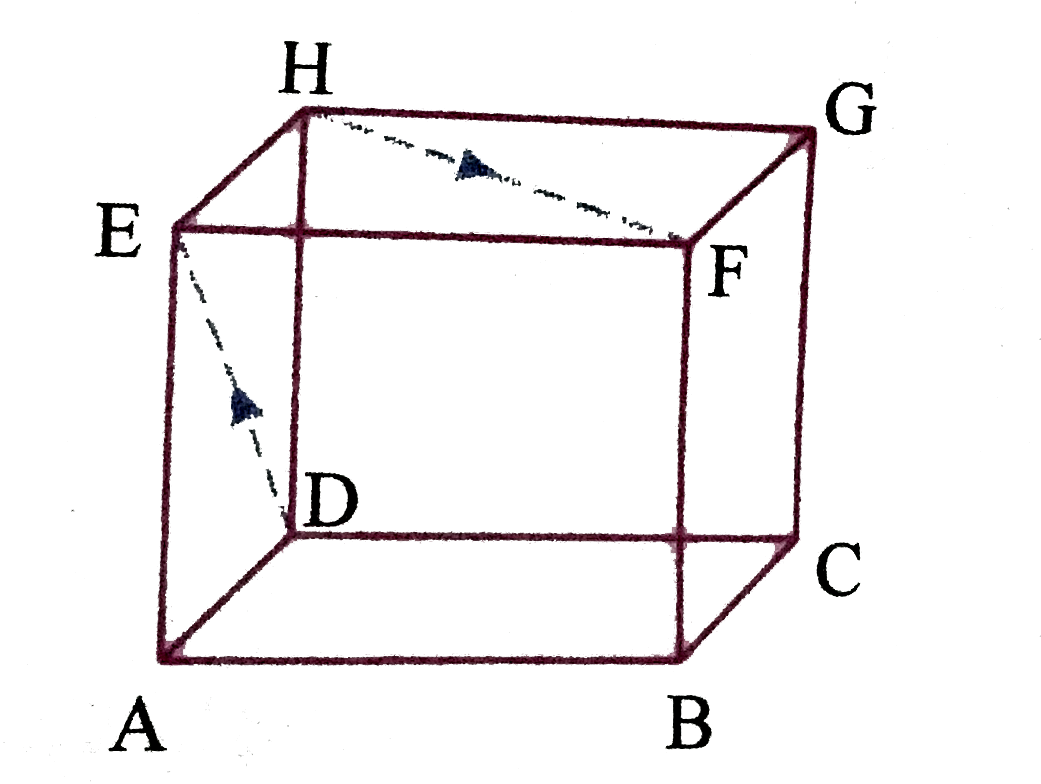 A(m+2m)a0B√5√2ma0C2ma0DMa0√2
A(m+2m)a0B√5√2ma0C2ma0DMa0√2Three solid spheres each of mass m and radius R are released from the position shown in figure. The speed of any one sphere at the time of collision would be
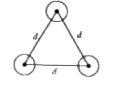 A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)
A√Gm(1d−3R)B√Gm(3d−1R)C√Gm(2R−1d)D√Gm(1R−2d)A block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
 A0.22 mB0.20 mCzeroD0.24 m
A0.22 mB0.20 mCzeroD0.24 m
Two identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
View SolutionA large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionFigure shows a flat car of mass M on a frictionless road. A small massless wedge is fitted on it as shown. A small ball of mass m is released from the top of the wedge, it slides over it and falls in the hole at distance l from the initial position of the ball. Find the distance the flat car moves till the ball gets into the hole.

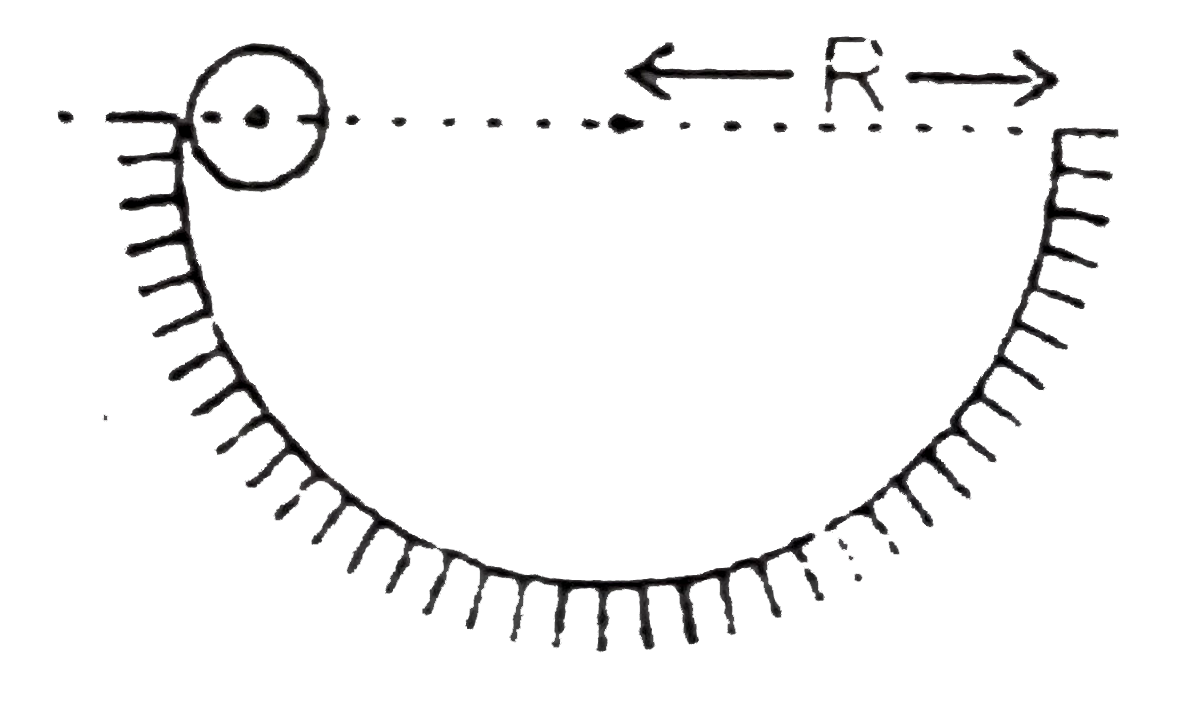
View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
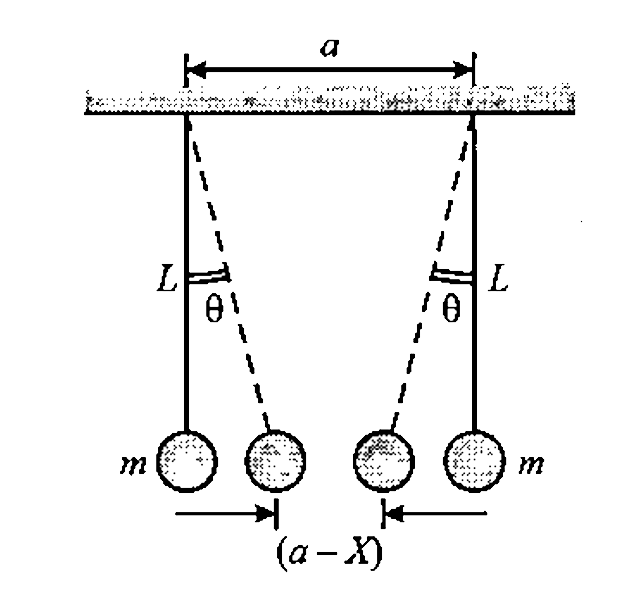
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
View Solution
