A turn of radius 20 m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
The correct Answer is:A, B, D
Banking angle, θ=tan−1(v2Rg)
36Km/h=10m/s
θ=tan−1(10020×9.8)=27∘
Angle of repose,
θr=tan−1(μ)=tan−1(0.4)=21.8∘
Sinne θ>θr , vehicle cannot remain in the given position with v=0 . At rest it will slide down. To find minimum speed, so that vehicle does not slip down, maixmum friction will act up the plane.
To find maximum speed, so that the vehicle does not skid up, maximum friction will act down the plane.
Minimum Speed
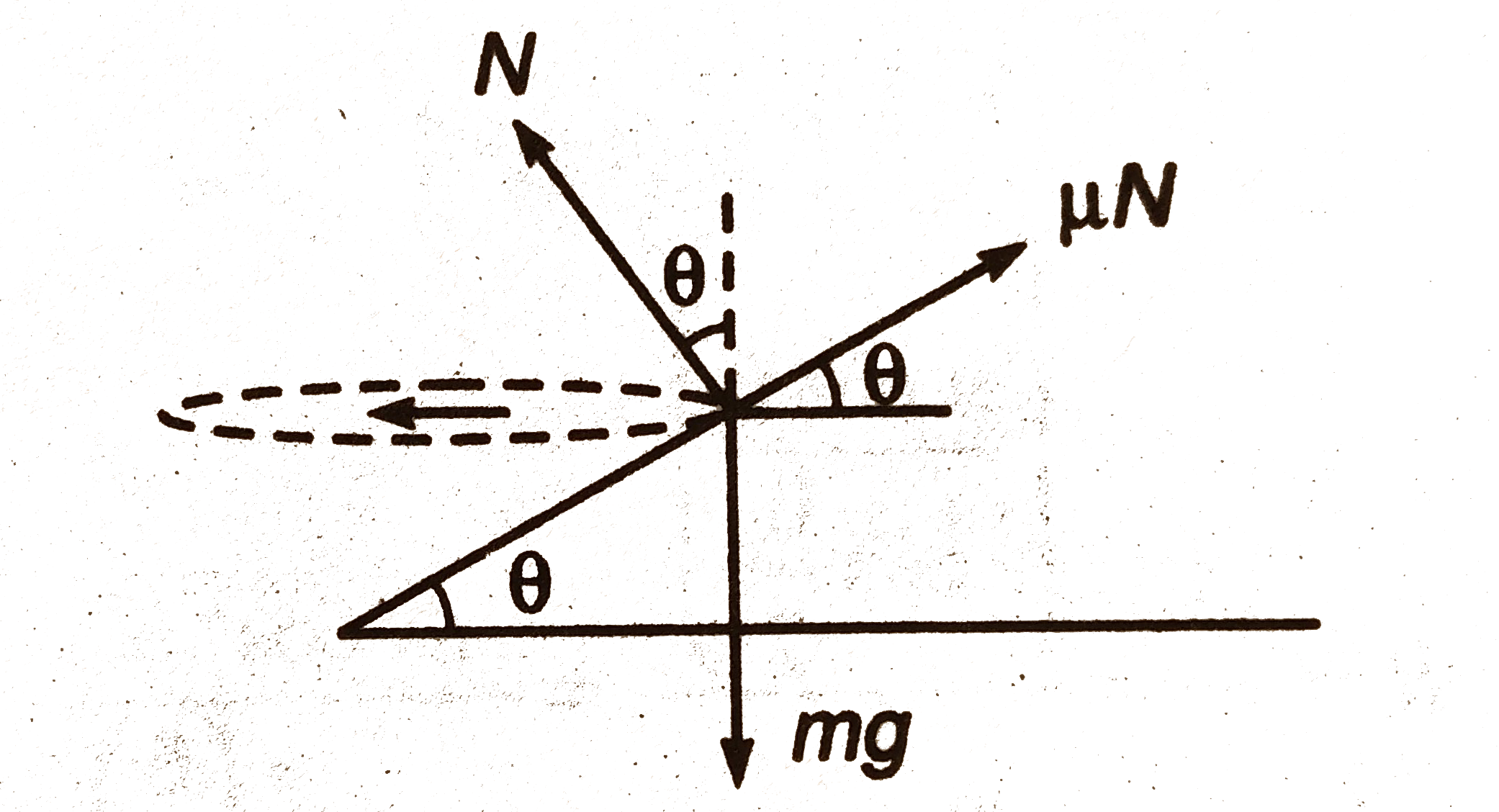
Equation of motion are,
Ncosθ+μNsinθ=mg ...(i)
Nsinθ−μNcosθ=mRv2max...(ii)
Solving these two equations, we get
vmin=4.2m/s
Maximum Speed ltbr> Equations of motion are, Ncosθ−μNsinθ=mg ...(iii)
Nsinθ+μNcosθ=mRv2max ...(iv)
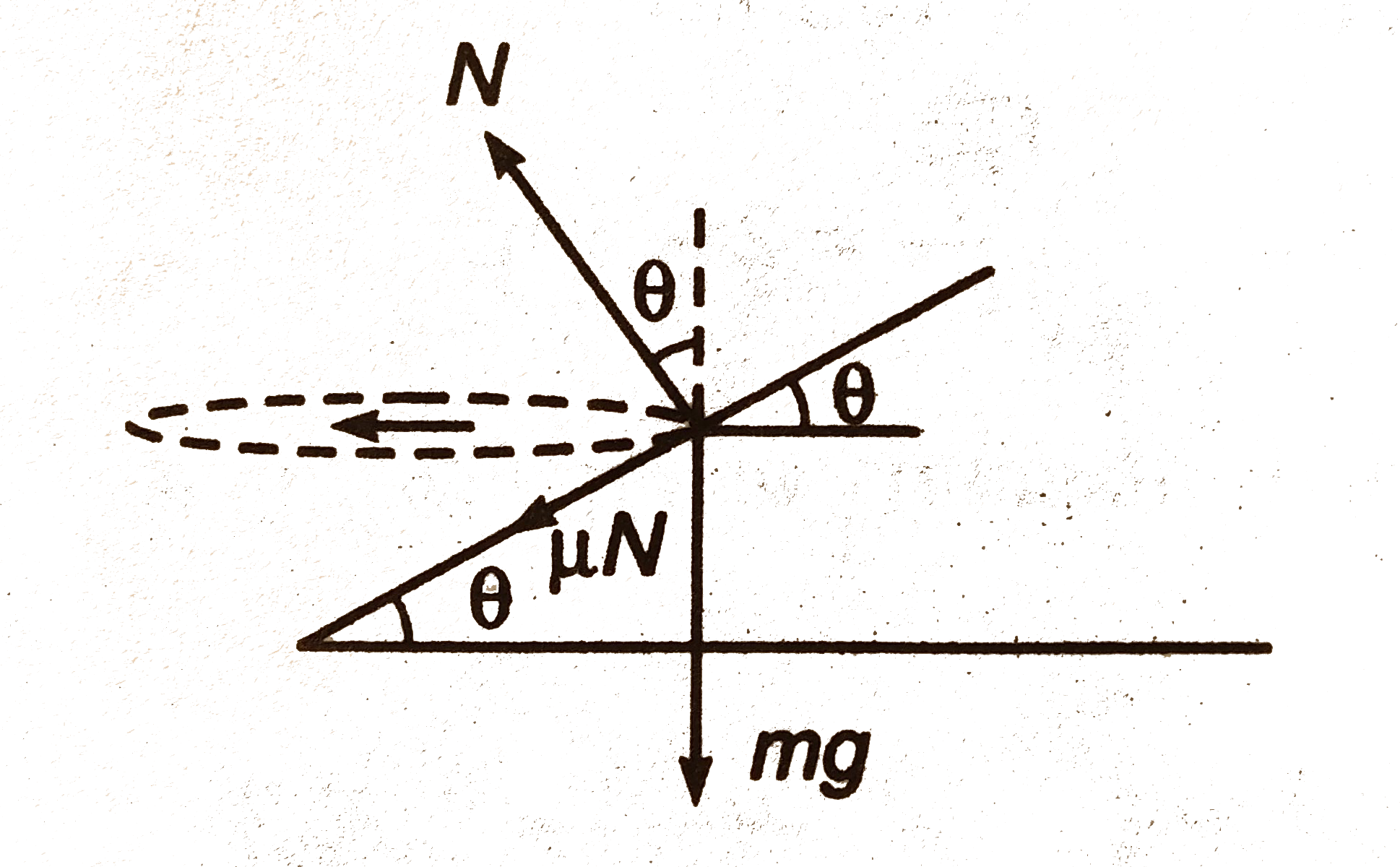
Solving two equations, we have
vmax=15m/s
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A cyclist speeding at 4.5km h−1 on a level road takes a sharp circular turn of radius 3 m without reducing the speed The coefficient of static friction between the road and the tyres is 0.1 will the cyclist slip while taking the turn (i) with a speed of 4.5km h−1 and (ii) with a speed of 9kmk−1?
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
View Solution
Knowledge Check
Consider a car moving along a straight horizontal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is
A30 mB40 mC72 mD20 mA motorcycle is travelling on a curved track of radius 500 m. If the coefficient of friction between road and tyres is 0.5, the speed avoiding skidding will be
A50 m/sB75 m/sC25 m/sD35 m/sA turn of radius 600 m is banked for a vehicle of mass 200 kg going with a speed of 180kmh−1 . Determine the banking angle of its path.
A22.6∘B19.8∘C30.6∘D40.8∘
A cyclist speeding at 4.5km h−1 on a level road takes a sharp circular turn of radius 3 m without reducing the speed The coefficient of static friction between the road and the tyres is 0.1 will the cyclist slip while taking the turn (i) with a speed of 405km h−1 and (ii) with a speed of 9kmk−1?
View SolutionA circular race track of radius 400 m is banked at an angle of 10∘ . If the coefficient of friction between the wheels of a race car and the road is 0.2 , what is the (i) optimum speed of the race car to aviod wear and tear on its tyres .
maximum permissible speed to aviod slipping ?
View SolutionA cyclist speeding at 4.5 km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The coefficient of static friction between the road and the tyres is 0.1.
(i) Will he slip while taking the turn?
(ii) Will he slip if his speed is 9 km/h?
View SolutionWhat would be the maximum speed of a car on a road turn of radius 30 m, if the coefficient of fraction between the types and the road is 0.4 ?
View SolutionConsider a car moving along a straight horizontal road with a speed of 36 km/h. If the coefficient of static friction between road and tyers is 0.4, the shortest distance in which the car can be stopped is (Take g=10m/s2)
View Solution