A ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2 . ltbr> 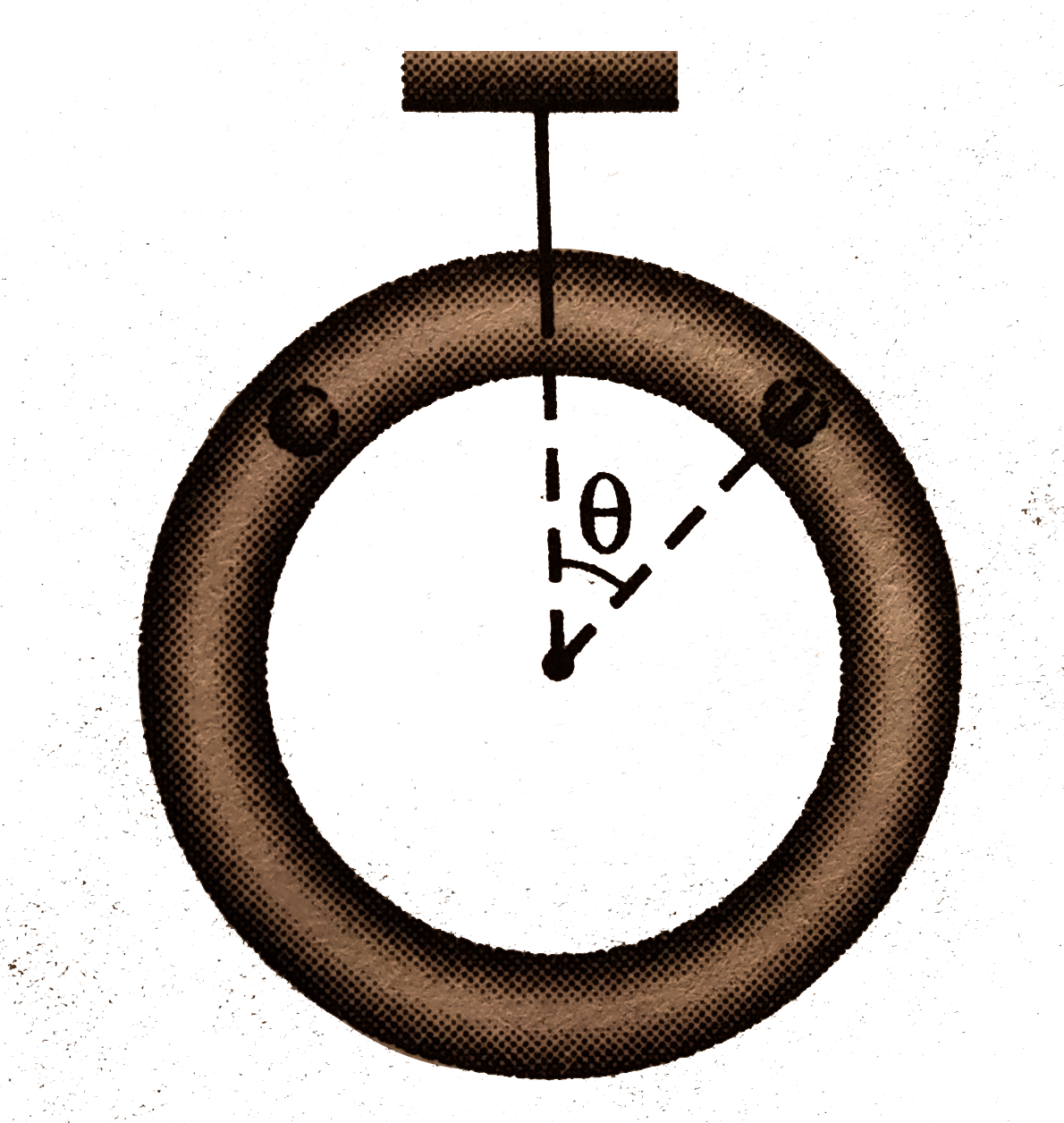
The correct Answer is:A
Let R be the radius of the ring
h=R(1−cosθ)
v2=2gh=2gR(1−cosθ)
mv2R=N+mgcosθ
or N=2mg(1−cosθ)=−mgcosθ
N=2mg−3mgcosθ
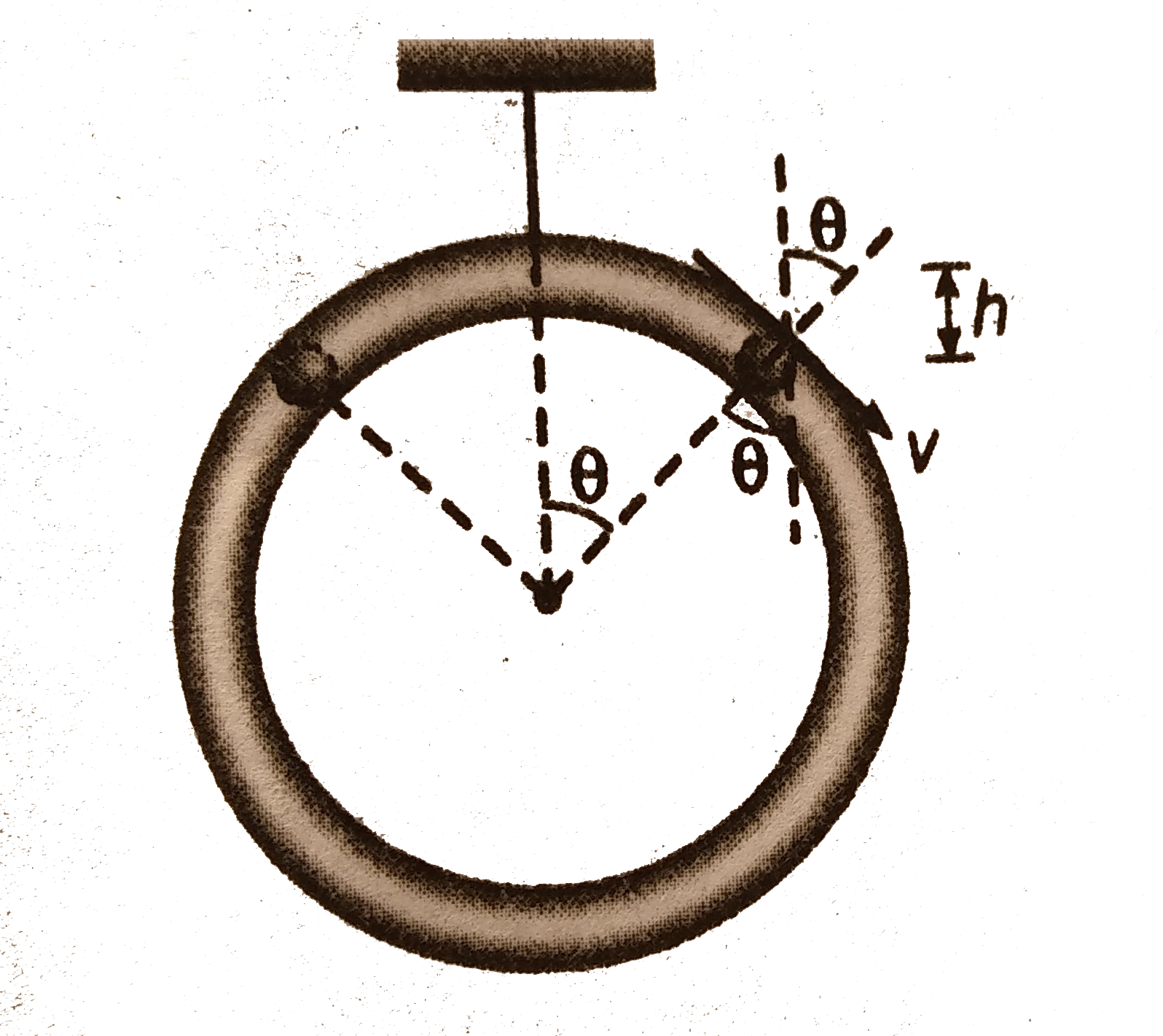
In the critical condition, tension in the string is zero and net upward force on the ring
F=2Ncosθ=2mg(2cosθ−3cos2θ) ...(i)
F is maximum when dFdthη=0
or −2sinθ+6sinθcosθ=0
or cosθ=13
Substituting in Eq. (i)
Fmax=2mg(2×13−3×19)=23mg
Fmax>Mg
or 23mg>Mg
or m>32M , Hence proved.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.

View SolutionA tube of mass M hangs from a thread and two balls of mass m slide inside it without friction (see figure). The balls are released simultaneously from the top of the ring and slide down on opposite sides. θ defines the positions of balls at any time as shown in figure
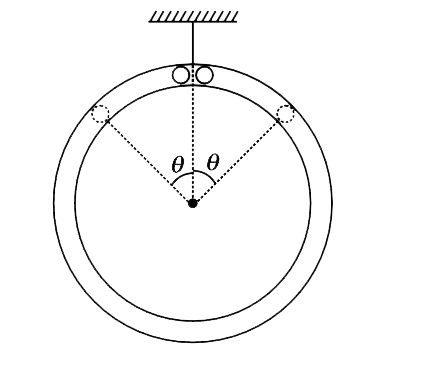
(a) Show that ring will start to rise if m≥3M2.
(b) If M=0 , find the angle θ at which the tube begins to rise.
View Solution
Knowledge Check
A cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination θ . Both are released simultaneously from the same height h.
Identify the correct statement(s)AThe friction force acting on the cylinder may be more than that acting on the ringBThe friction force acting on the ring may be more than that acting on the cylinderCIf the friction is sufficient to roll the cylinder then the ring will also rollDIf the friction is sufficient to roll the ring then the cylinder will also rollA cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination θ . Both are released simultaneously from the same height h.
When these bodies roll down to the foot of the inclined plane, thenAthe mechanical energy of each body is conservedBthe velocity of centre of mass of the cylinder is 2√gh3Cthe velocity of centre of mass of the ring is √ghDthe velocity of centre of mass of each body is √2ghA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
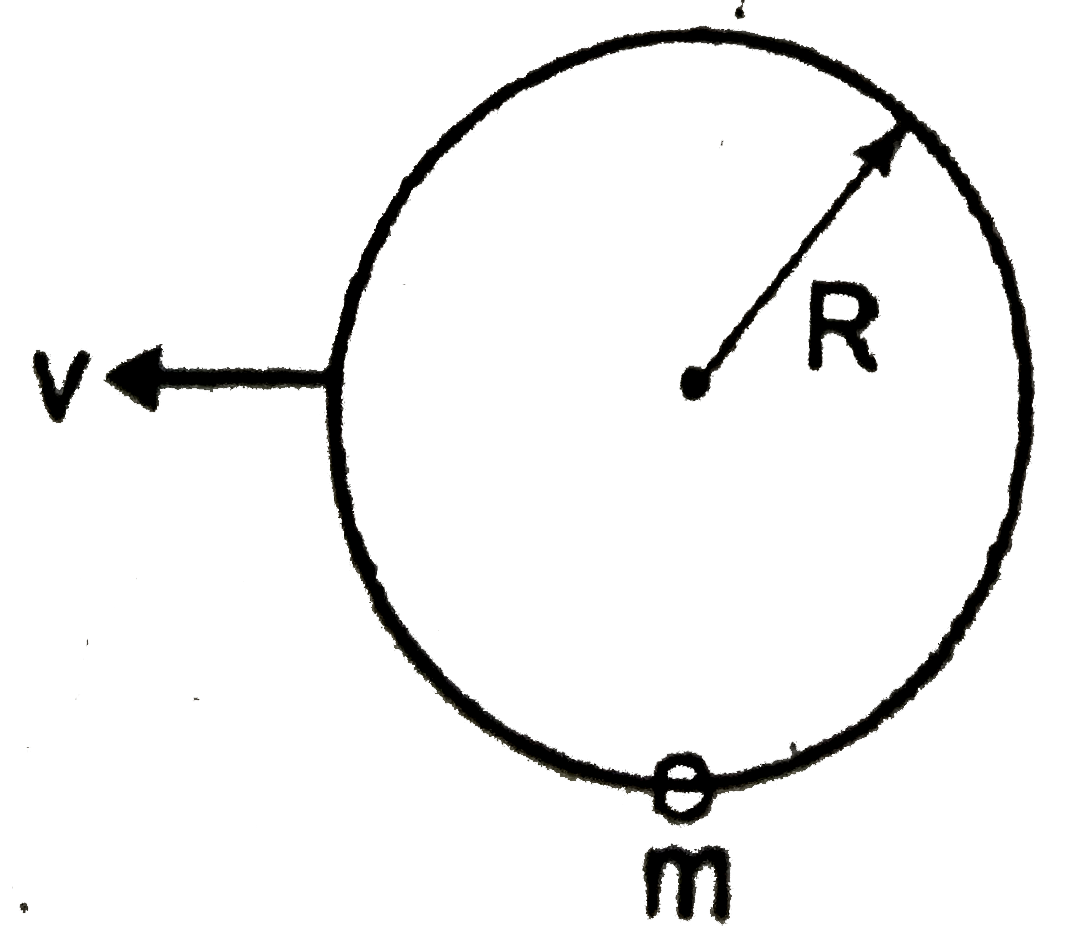 A√3gRB√4gRC√5gRD√5.5gR
A√3gRB√4gRC√5gRD√5.5gR
Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if m>3M2. If m = 2M, at what angle θ from vertical this happends ?
(a)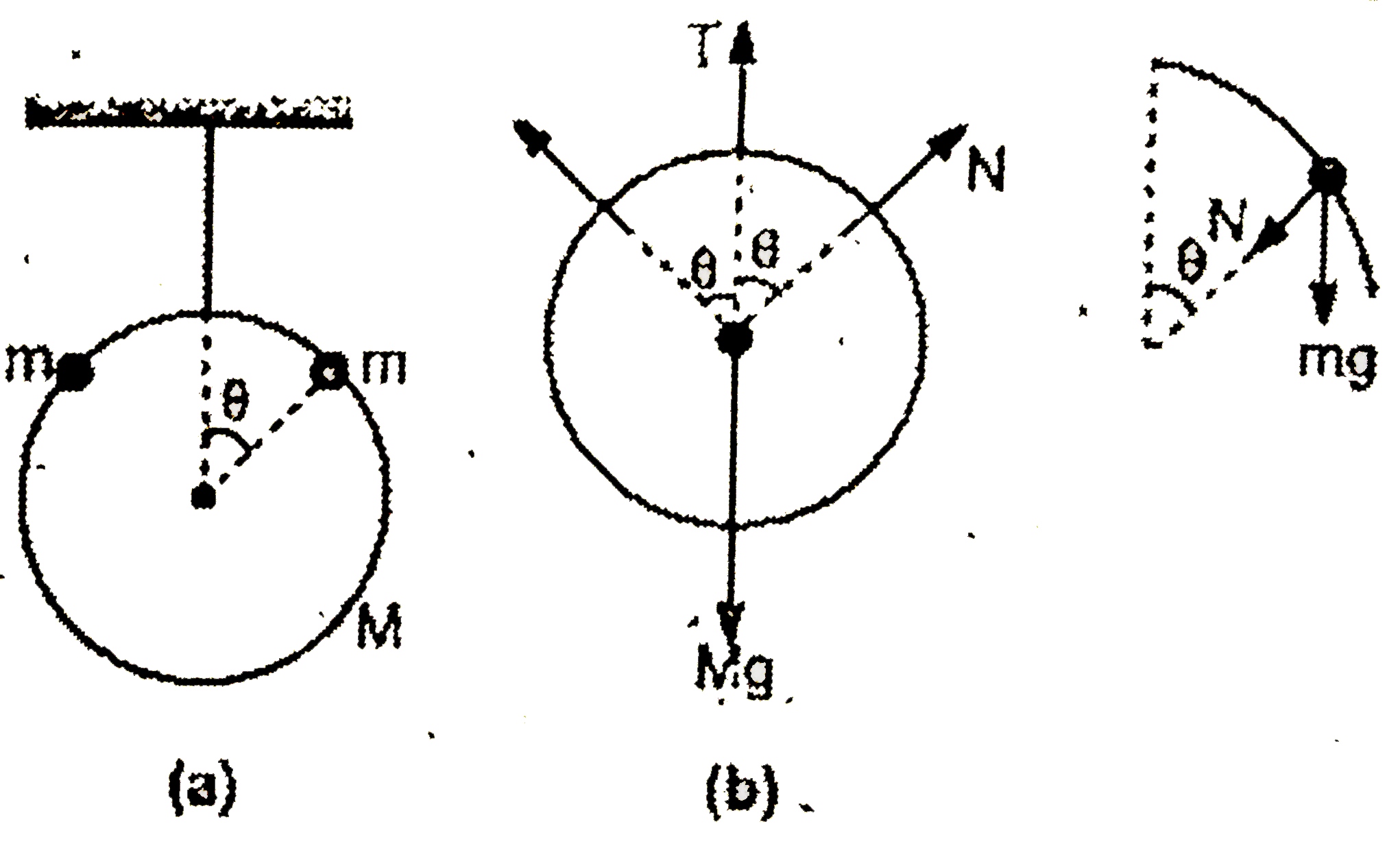
View SolutionA and B are two identical rings released from the top of an inclined plane . A slides down and B rolls down. Then which reaches the bottom first ?
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?

View SolutionA small cube of mass m slides down a circular path of radius R cut into a large block of mass M. M rests on a table and both blocks move without friction. The blocks initially are at rest and m starts from the top of the path. Find the velocity v of the cube as it leaves the block.
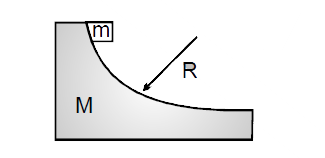
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :

View Solution
