A partical of mass 1kg rests on rought contact with a plane inclined at 30∘ to the horizontal and is just about to slip, Find the coefficient of friction between the plane and the particle.
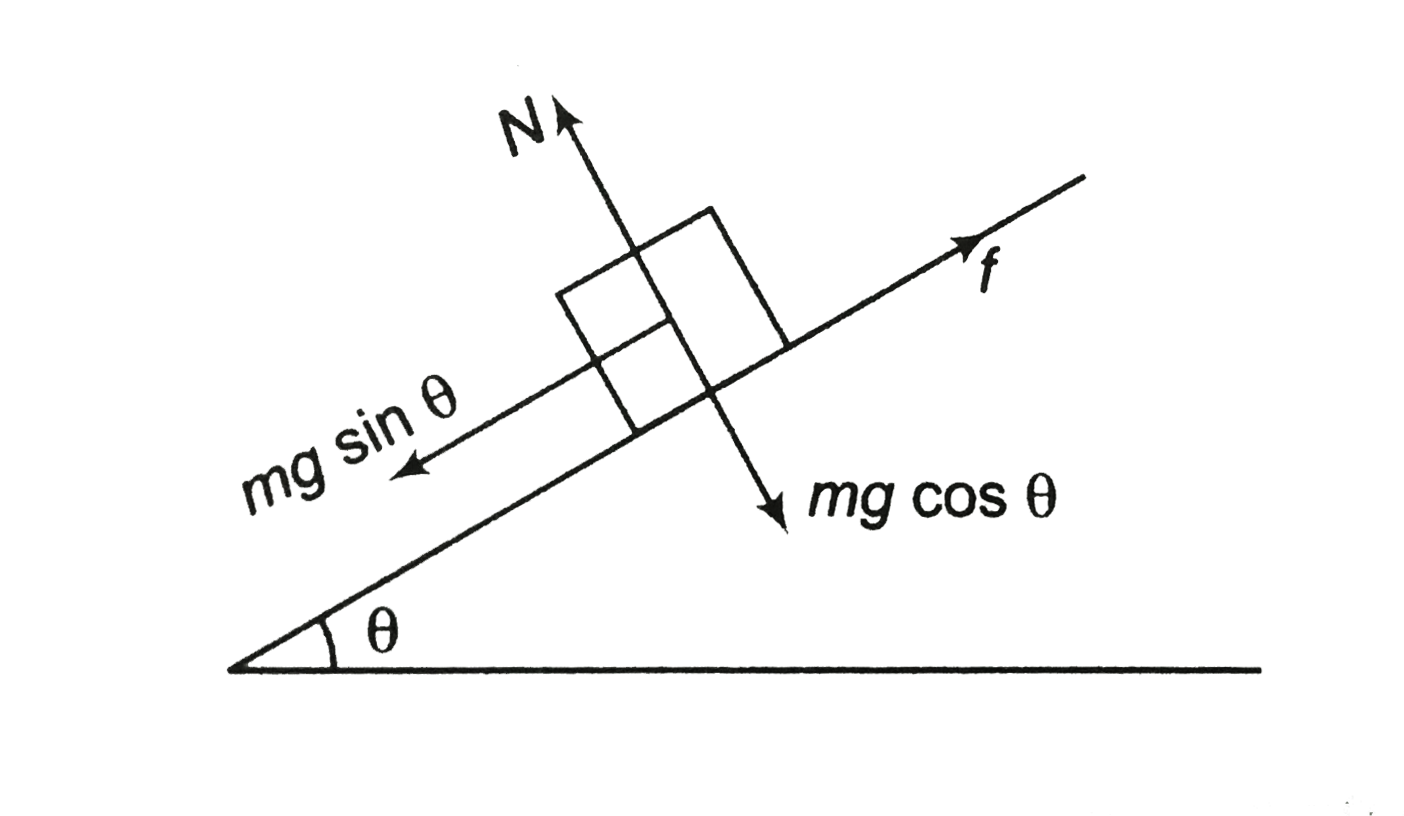
Weight mg has two components mgsinθ and mgcosθ.Block is at rest
:. N=mgcosθ …(i)
f=mgsinθ …(ii)
Block is about to slip.
:. f=fl=μN …(iii)
Here μs=μ
Solving these three equations, we get
μ=tanθ=tan30∘
=1√3
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
Knowledge Check
A body takes just twice the time as long to slide down a plane inclined at 30∘ to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is
A√34B√3C43D34A body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
A0.346B0.921C1.926D2.912A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
Two masses 6 kg and 4 kg are connected by a flexible inextensible string rest on an inclined plane inclined at 60∘ with the horizontal as shown in figure. The coefficient of friction between the plane and the 6kg mass is 0.1 and the between the plane and the 4 kg massis 0.6 .
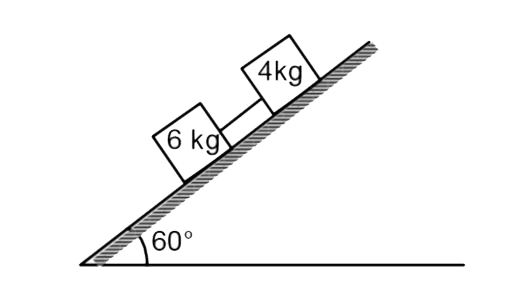
Find the tension in the connecting string.
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View SolutionA ball of mass M and radius R is released on a rough inclined plane of inclination θ. Friction is not sufficient to prevent slipping. The coefficient friction between the ball and the plane is μ. Find
(a). The linear acceleration of the ball down the plane.
(b). the angular acceleration of the ball about its centre of mass.
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution
