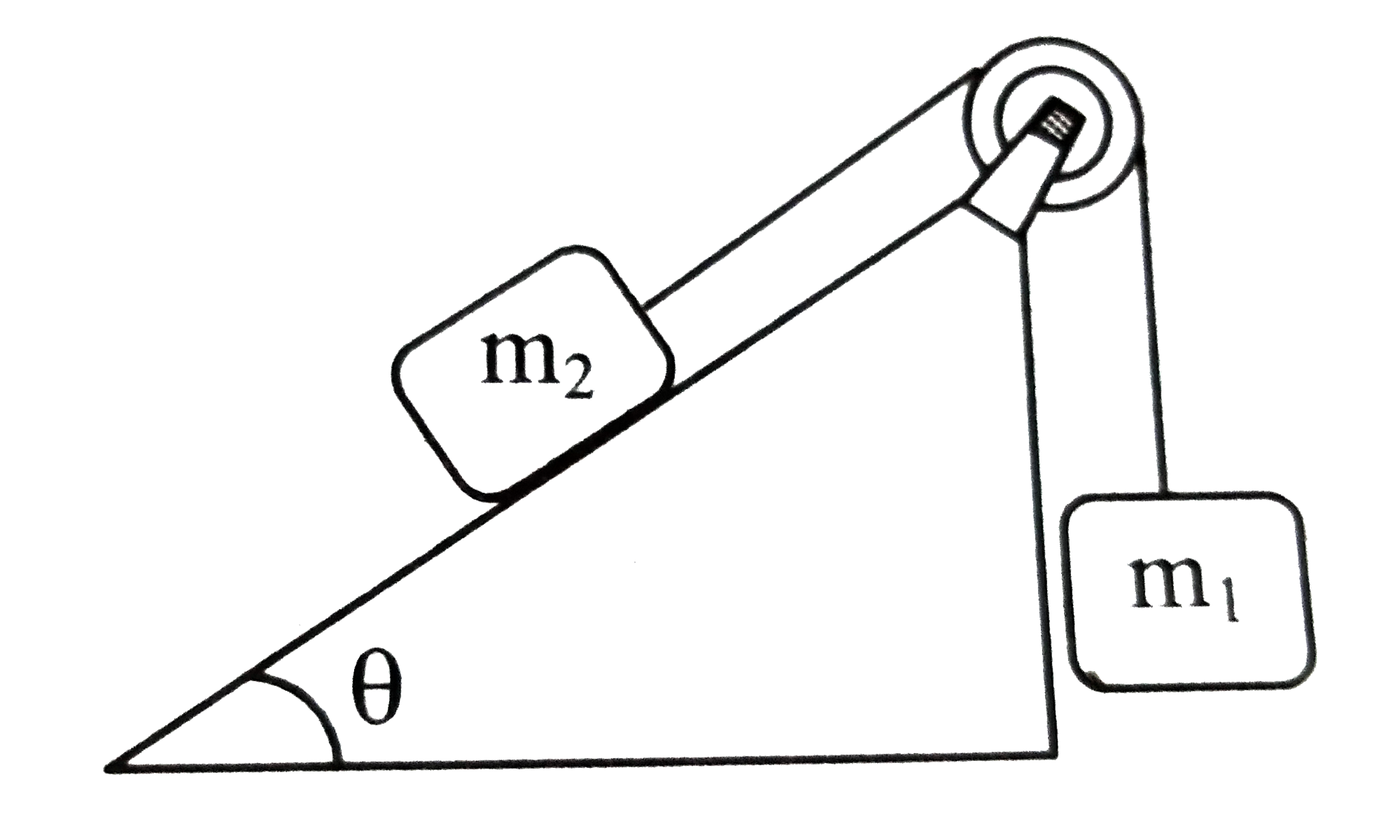
The two blocks A and B of equal mass are initially in contact when released from rest on the inclined plane. The coefficients of friction between the inclined plane and A and B are and respectiely. Friction is not sufficient to prevent slipping.

If , the blocks will always remain in contact
If , the blocks will slide down with different accelerations
If , the blocks will have a common acceleration
If the blocks will have a common acceleration
The correct Answer is:A, B, C
and
is common and R is positive if
and if then they no longer remain in contact, A and B slides down with acceleration and respectively.
Similar Questions
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θWhen a body slides down an inclined plane with coefficient of friction as μk, then its acceleration is given by .
Ag(μksinθ+cosθ)Bg(μksinθ−cosθ)Cg(μksinθ+μkcosθ)Dg(sinθ−μkcosθ)When a body slides down an inclined plane with coefficient of friction as μk then its acceleration is given by
Ag(μksinθ+cosθ)Bg(μksinθ−cosθ)Cg(sinθ+μkcosθ)Dg(sinθ−μkcosθ)
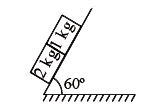
In the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View SolutionTwo blocks are in contect moving on an inclined plane of inclination α with the horizontal. The masses of the blocks are equal to m1 and m2 and the coefficients of friction between the inclined plane and the blocks are equal to μ1 and μ2(μ1>μ2) respectively. Find (a) common acceleration of the blocks and (b) the contact force between the blocks.

View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View Solution