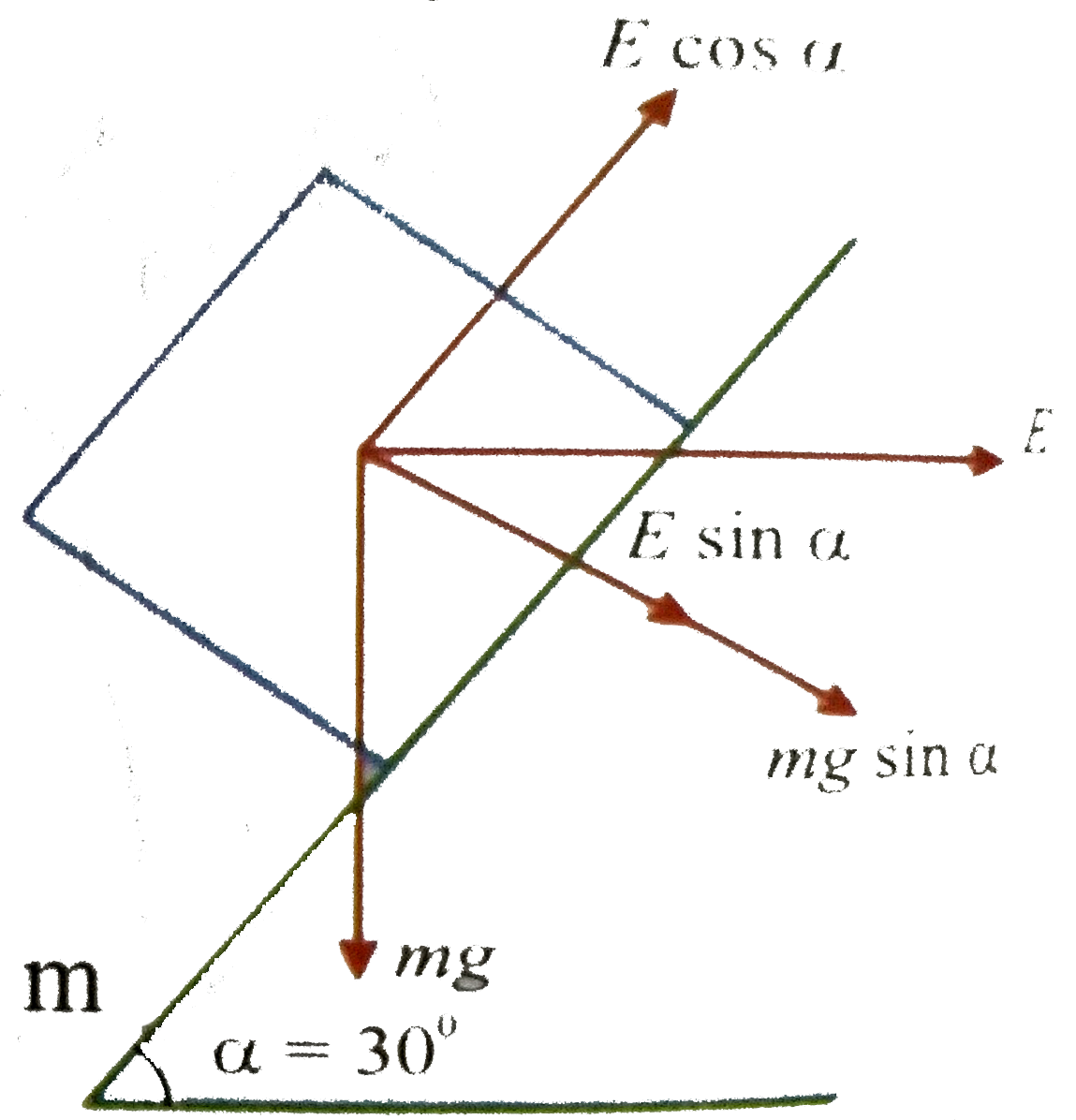
A partical of mass 1kg and carrying 0.01C is at rest on an inclined plane of angle 30∘ with horizontal when an electric field of 490√3NC−1 applied parallel to horizontal .The cofficient of friction is
0.5
1√3
√32
√37
The correct Answer is:4
To find the coefficient of friction for the given problem, we will follow these steps:
Step 1: Identify the forces acting on the particle
The forces acting on the particle are:
1. Gravitational force (mg) acting downwards.
2. Electric force (F_e = qE) acting horizontally due to the electric field.
3. Normal force (N) acting perpendicular to the inclined plane.
4. Frictional force (F_f) acting parallel to the inclined plane opposing the motion.
Step 2: Break down the gravitational force
The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
Where:
- m=1kg
- g=9.8m/s2
- θ=30∘
Calculating these components:
- mg=1×9.8=9.8N
- mgcos30∘=9.8×√32=4.9√3N
- mgsin30∘=9.8×12=4.9N
Step 3: Calculate the electric force
The electric force acting on the particle is given by:
Fe=qE
Where:
- q=0.01C
- E=490√3N/C
Calculating the electric force:
Fe=0.01×490√3=4.9√3N
Step 4: Set up the equations for normal force and friction
The normal force N can be expressed as:
N=mgcosθ+qEsinθ
Substituting the values:
N=4.9√3+4.9√3×12
N=4.9√3+4.92√3
N=4.9√3+4.92√3=9.8√32+4.92√3=9.8√3+4.92√3
Step 5: Balance the forces along the incline
Since the particle is at rest, the forces along the incline must balance:
mgsinθ=Ff+qEcosθ
Where Ff=μN.
Substituting the values:
4.9=μN+4.9√3×√32
4.9=μN+4.92
μN=4.9−2.45=2.45
Step 6: Solve for the coefficient of friction μ
Now substituting for N:
μ=2.45N=2.459.8√3+4.92√3
μ=2.45⋅2√39.8√3+4.9
Step 7: Simplify and calculate μ
After simplification, we find:
μ=4.9√37
Final Answer
Thus, the coefficient of friction μ is:
μ=√37
---
The forces acting on the particle are:
1. Gravitational force (mg) acting downwards.
2. Electric force (F_e = qE) acting horizontally due to the electric field.
3. Normal force (N) acting perpendicular to the inclined plane.
4. Frictional force (F_f) acting parallel to the inclined plane opposing the motion.
The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- m=1kg
- g=9.8m/s2
- θ=30∘
- mg=1×9.8=9.8N
- mgcos30∘=9.8×√32=4.9√3N
- mgsin30∘=9.8×12=4.9N
The electric force acting on the particle is given by:
Fe=qE
Where:
- q=0.01C
- E=490√3N/C
Fe=0.01×490√3=4.9√3N
The normal force N can be expressed as:
N=mgcosθ+qEsinθ
Substituting the values:
N=4.9√3+4.9√3×12
N=4.9√3+4.92√3
N=4.9√3+4.92√3=9.8√32+4.92√3=9.8√3+4.92√3
Since the particle is at rest, the forces along the incline must balance:
mgsinθ=Ff+qEcosθ
Where Ff=μN.
4.9=μN+4.9√3×√32
4.9=μN+4.92
μN=4.9−2.45=2.45
Now substituting for N:
μ=2.45N=2.459.8√3+4.92√3
μ=2.45⋅2√39.8√3+4.9
After simplification, we find:
μ=4.9√37
Thus, the coefficient of friction μ is:
μ=√37
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1
Explore 8 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 2
Explore 10 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level II(C.W)
Explore 27 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View SolutionA spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
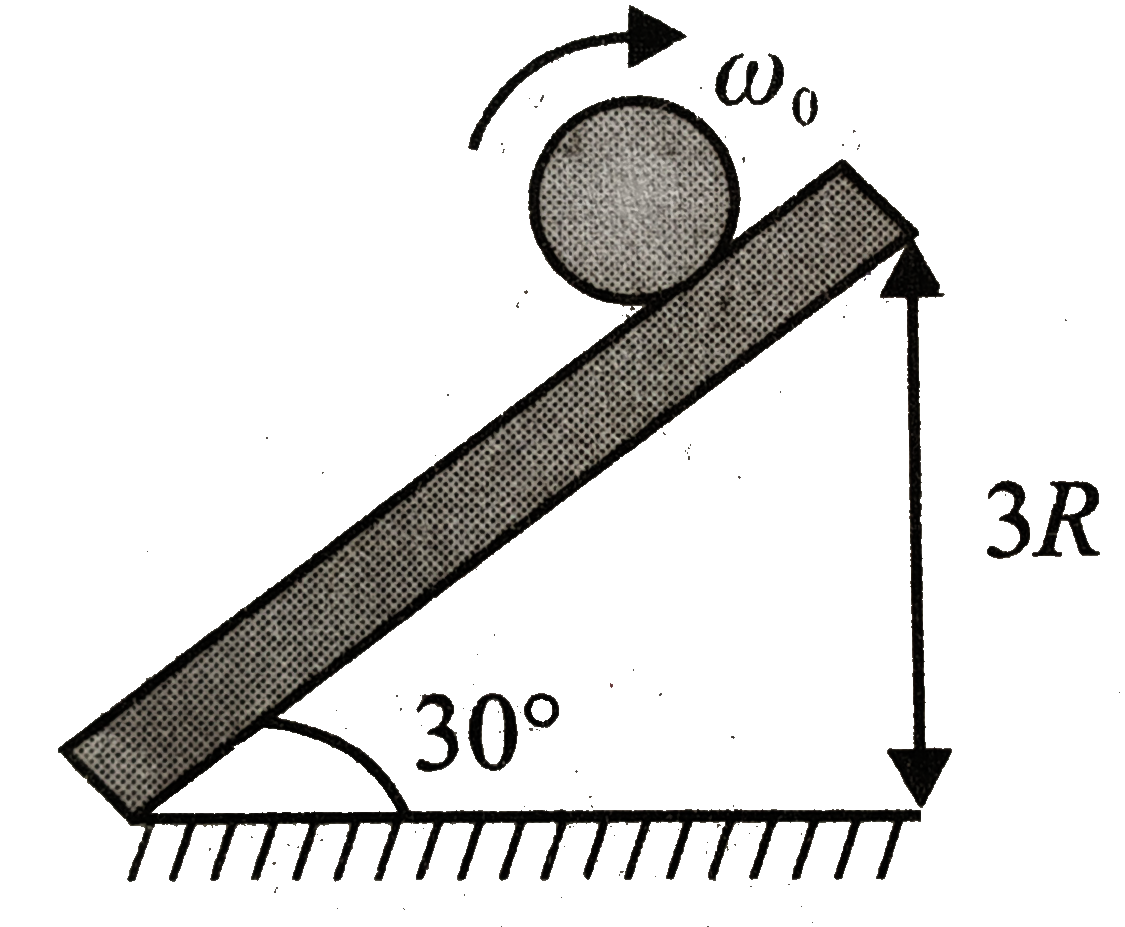
View Solution
Knowledge Check
A particle of mass 1kg and carrying 0.01C is at rest on an inclined plane of angle 30∘ with horizontal when an electric field of 490√3NC−1 applied parallel to horizontal .The coefficient of friction is
A0.5B1√3C√32D√37A particles of mass 1kg and carrying positive charge 0.01C is sliding down an inclined plane of angle 30∘ with the horizontal .An electric field E is applied to stop the particles.If the coefficient of friction between the particles and the surface of the plane is 12√3 E must be
 A1260V/mB245V/mC140√3V/mD490√3V/m
A1260V/mB245V/mC140√3V/mD490√3V/mA particles of mass 1kg and carrying positive charge 0.01C is sliding down an inclined plane of angle 30∘ with the horizontal .An electric field E is applied to stop the particles.If the coefficient of friction between the particles and the surface of the plane is 12√3. E must be
 A1260 V/mB245 V/mC140√3V/mD490√3 V/m
A1260 V/mB245 V/mC140√3V/mD490√3 V/m
A brick of mass 2kg just begins to slide down on inclined plane at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionA brick of mass 2kg begins to slide down on a plane inclined at an angle of 45∘ with the horizontal. The force of friction will be
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
View SolutionA block of mass 2kg is pushed down an inclined plane of angle 37∘ above horizontal with a force parallel to inclined plane. The coefficient of friction is (3)/(4). The block moves 10m in 2 seconds starting form rest. The magnitude of the force is
View Solution

