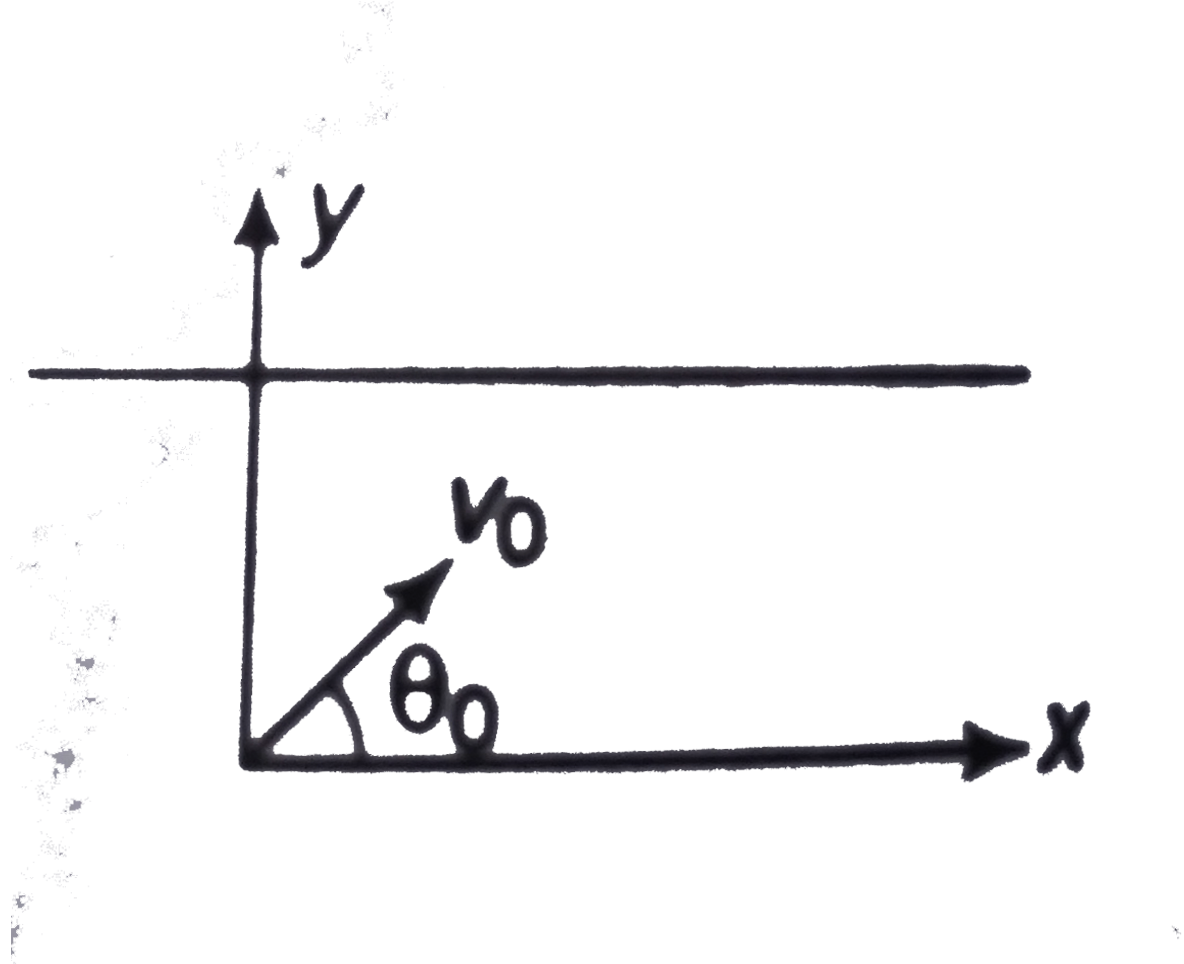
A projectile of mass m is fired into a liquid at an angle $θ_{0}$ with an initial velocity $v_{0}$ as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i. e. $F = - k v$ where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance $x_{max}$ that it travels?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

$a_{x} = \frac{d v_{x}}{d t} = - \frac{k v cos θ}{m} = - \frac{k}{m} v_{x}$
$∴ \frac{d v_{x}}{v_{x}} = - \frac{k}{m} d t or \int_{v_{0} {cos θ}_{0}}^{v_{x}} \frac{d v_{x}}{v_{x}} = - \frac{k}{m} \int_{0}^{t} d t$
or $v_{x} = v_{0} {cos θ}_{0} e^{- \frac{k}{m} t}$ …(i)

Similarly,
$a_{y} = \frac{d v_{y}}{d t} = - \frac{k v sin θ}{m} - g = - (\frac{k}{m} v_{y} + g)$
or $\int_{v_{0} {sin θ}_{0}}^{v_{y}} \frac{d v_{y}}{\frac{k}{m} v_{y} + g} = - \int_{0}^{t} d t$
or $\frac{m}{k} {[ln (\frac{k}{m} v_{y} + g)]}_{v_{0} {sin θ}_{0}}^{v_{y}} = - t$
or $\frac{(\frac{k}{m} v_{y} + g)}{(\frac{k}{m} v_{0} {sin θ}_{0} + g)} = e^{- \frac{k}{m} t}$
or $v_{y} = \frac{m}{k} [(\frac{k}{m} v_{0} {sin θ}_{0} + g) e^{- \frac{k}{m} t} - g]$ ...(ii)
(b) Eq. (i) can be written as
$\frac{d x}{d t} = v_{0} {cos θ}_{0} e^{- \frac{k}{m} t}$
or $\int_{0}^{x} d x = v_{0} {cos θ}_{0} \int_{0}^{t} e^{- \frac{k}{m} t} d t$
or x=(m v_0 cos theta_0)/k [1-e^(-k/m t)] $< b r > or$ x_m=(m v_0 cos theta_0)/k $< b r > a t$ t=oo

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A projectile of mass $m$ is launched with an initial velocity ${\to v}_{i}$ making an angle $θ$ with the horizontal as shown in figure. The projectile momentum of the particle about the origin when it is at the highest point of its trajectory is.
.
A $\frac{- m_{i}^{3} {sin θ}^{2} cos θ}{2 g} ˆ k$
B $\frac{m_{i}^{3} {sin θ}^{2} cos θ}{2 g} ˆ k$
C $\frac{- m_{i}^{3} {sin θ}^{2} cos θ}{g} ˆ k$
D $\frac{2 m_{i}^{3} {sin θ}^{2} cos θ}{g} ˆ k$
Question 2 - Select One
A projectile is fired from the origin with a velocity $v_{0}$ at an angle $θ$ with x-axis. The speed of the projectile at an altitude $h$ is .
A $v_{0} cos θ$
B $\sqrt{v_{0}^{2} - 2 g h}$
C $\sqrt{v_{0}^{2} {sin}^{2} θ - 2 g h}$
DNone of these
Question 3 - Select One
A projectile is fired at an angle of $30^{\circ}$ with the horizontal such that the vertical component of its initial velocity is 80m/s. Find approximatly the velocity of the projectile at time $T / 4$ where T is time of flight.
A $180 m / s$
B $155 m / s$
C $145 m / s$
D $140 m / s$

DC PANDEY-KINEMATICS-Subjective Questions

Home
Ask Doubt
Profile