A river of width $ω$ is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If $P Q = Q R = ω,$ find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.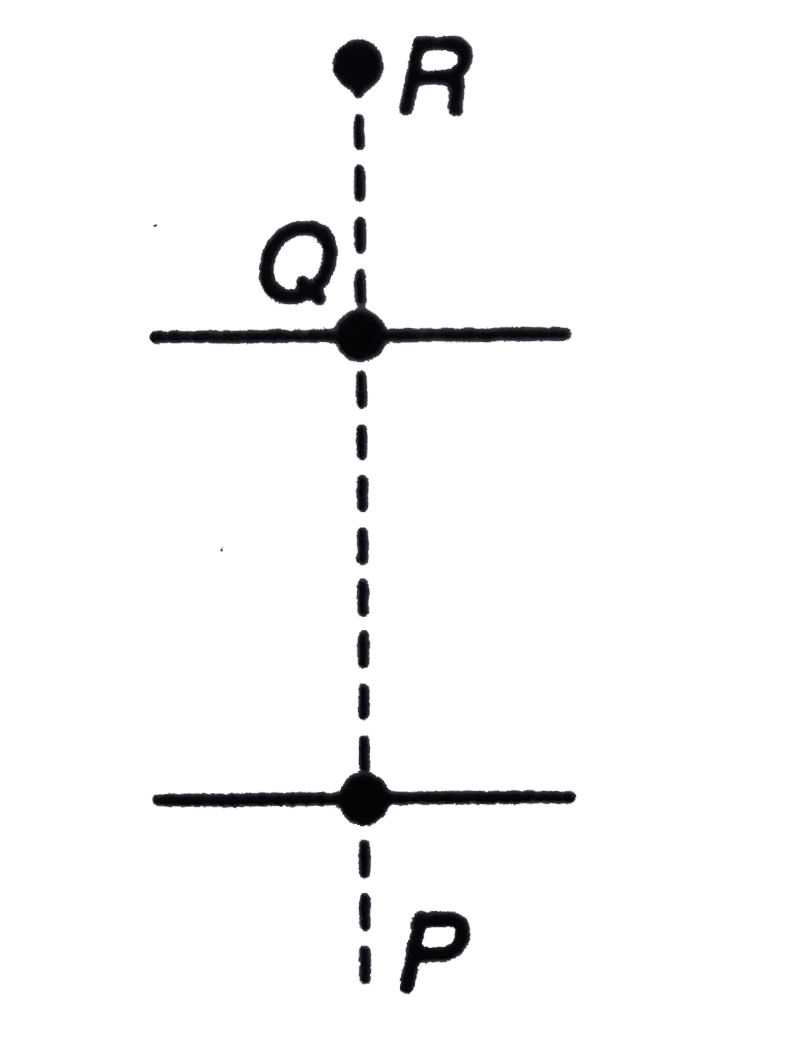

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

(a) Since, the resultant velocity is always
perpendicular to the line joining boat and R, the boat
is moving in a circle of radius $2 ω$ and centre at R.

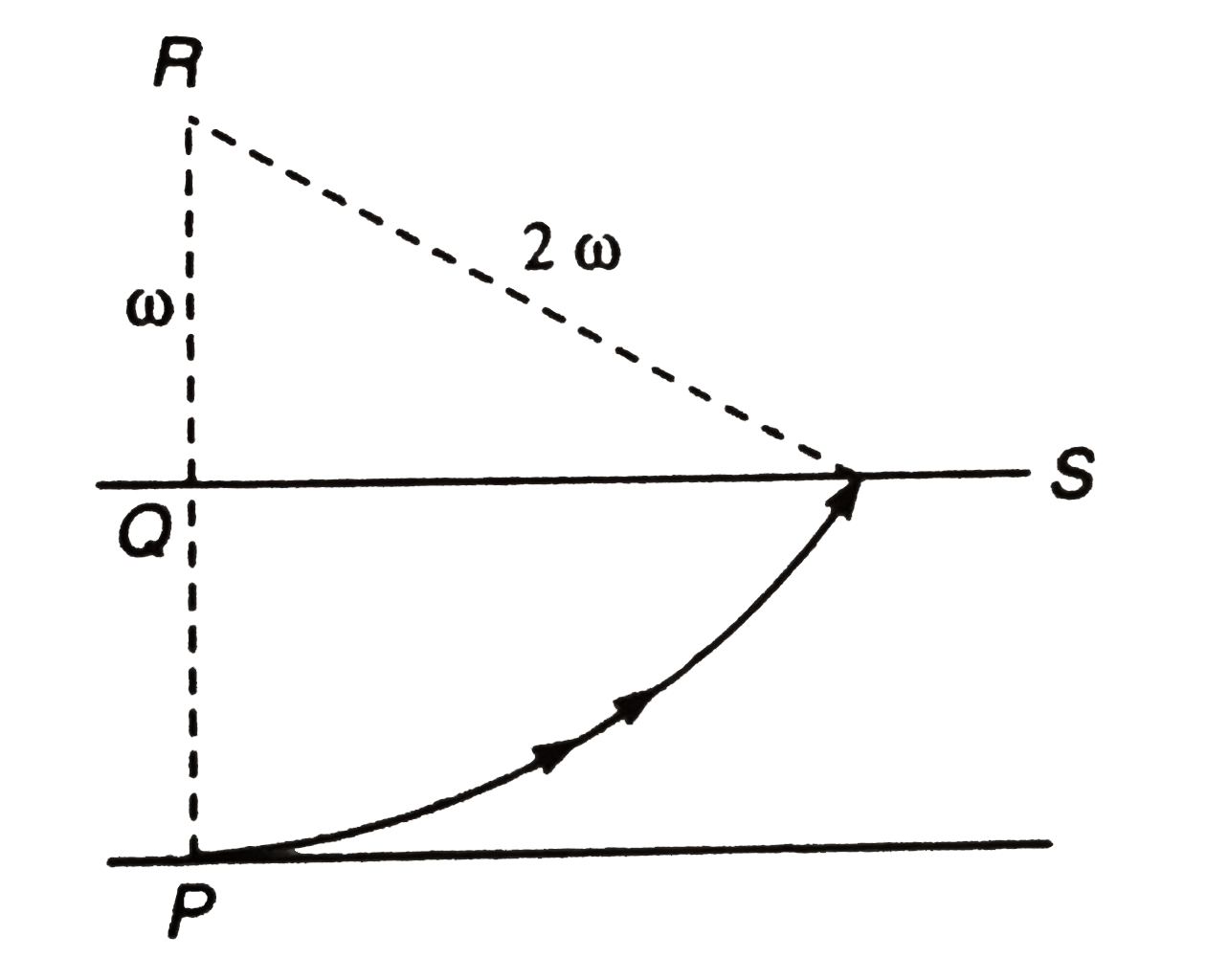
(b) Drifting = $Q S = \sqrt{4 ω^{2} - ω^{2}} = \sqrt{3} ω$ .
(c) Suppose at any arbitrary time, the boat is at
point B.

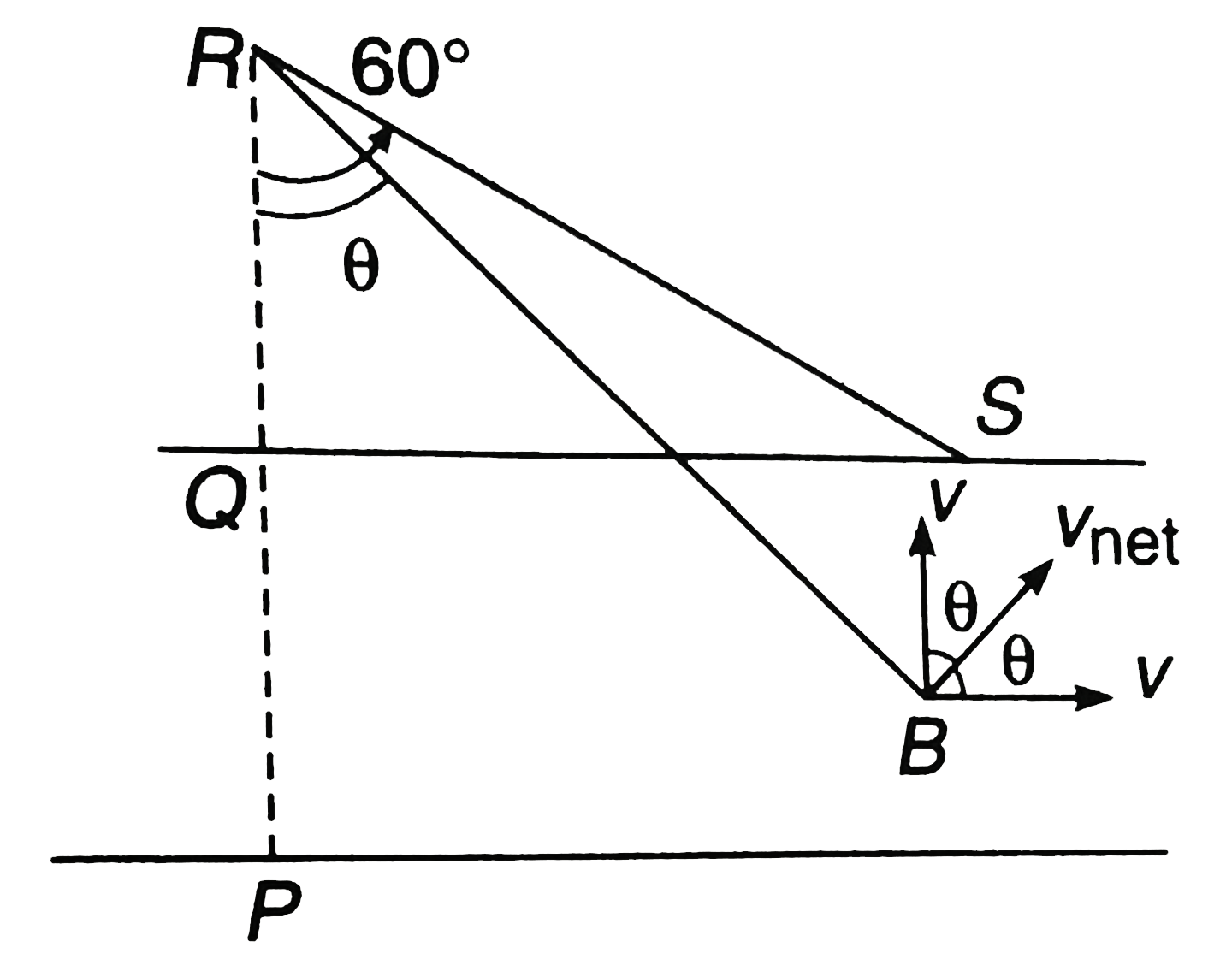
$V_{net} = 2 V cos θ$
$\frac{d θ}{d t} = \frac{V_{net}}{2 ω} = \frac{v cos θ}{ω}$
or $\frac{ω}{v} sec θ d θ = d t$
$∴ \int_{0}^{t} d t = \frac{ω}{v} \int_{0}^{60^{\circ}} sec θ d θ$
$∴ \frac{ω}{v} [\in {(sec θ + tan θ]}_{0}^{60^{\circ}}$
or $t = \frac{1.317 ω}{v}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
River is flowing with a velocity $v_{B R} = 4 ˆ i m / s$ . A boat is moving with a velocity of $v_{B R} = (- 2 ˆ i + 4 ˆ j) m / s$ relative to river. The width of the river is $100 m$ along $y$ -direction. Choose the correct alternative(s)
AThe boatman will cross the river in $25 s$
BAbsolute velocity of boatman is $2 \sqrt{5} m / s$
CDrift of the boatman along the river current is $50 m$
DThe boatman can never cross the river
Question 2 - Select One
A boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
A $30^{\circ}$
B $60^{\circ}$
C $150^{\circ}$
D $120^{\circ}$
Question 3 - Select One or More
A man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
AMan can directly reach point B in time d/l.
BMan can cross the river in minimum time d/v
CMan can reach point B directly in time $\frac{d}{\sqrt{v^{2} - u^{2}}}$
DIf $u > v$ then man cannot reach the point B directly .

DC PANDEY-KINEMATICS-Subjective Questions

Home
Ask Doubt
Profile