A man with some passengers in his boat, starts perpendicular to flow of river 200 m wide and flowing with $2 m / s .$ Speed of boat in still water is $4 m / s .$ When he reaches half the width of river the passengers asked him that they want to reach the just opposite end from where they have started.
(a) Find the direction due which he must row to reach the required end.
(b) How many times more time, it would take to that if he would have denied the passengers?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) $v_{b r} = 4 m / s, v_{r} = 2 m / s$
$tan θ = \frac{B C}{A B} = \frac{| v_{r} |}{| v_{b r} |} = \frac{2}{4} = \frac{1}{2}$

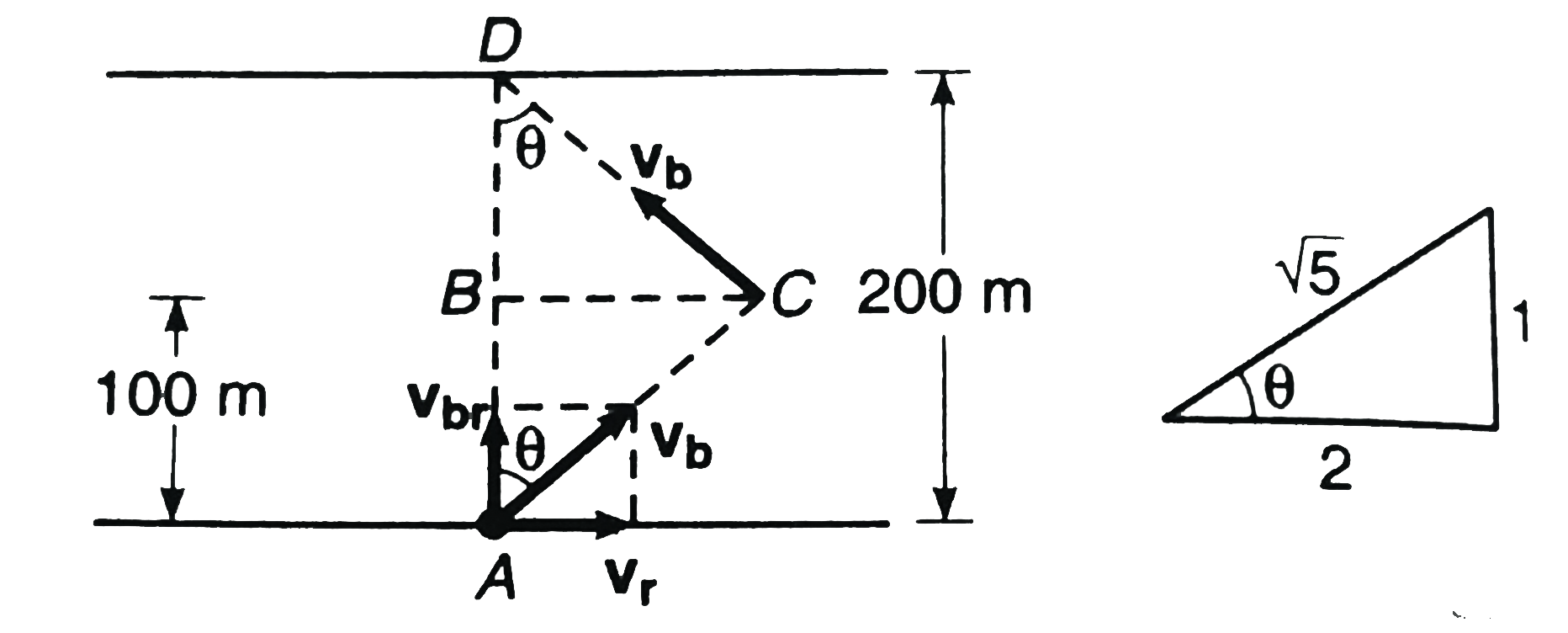
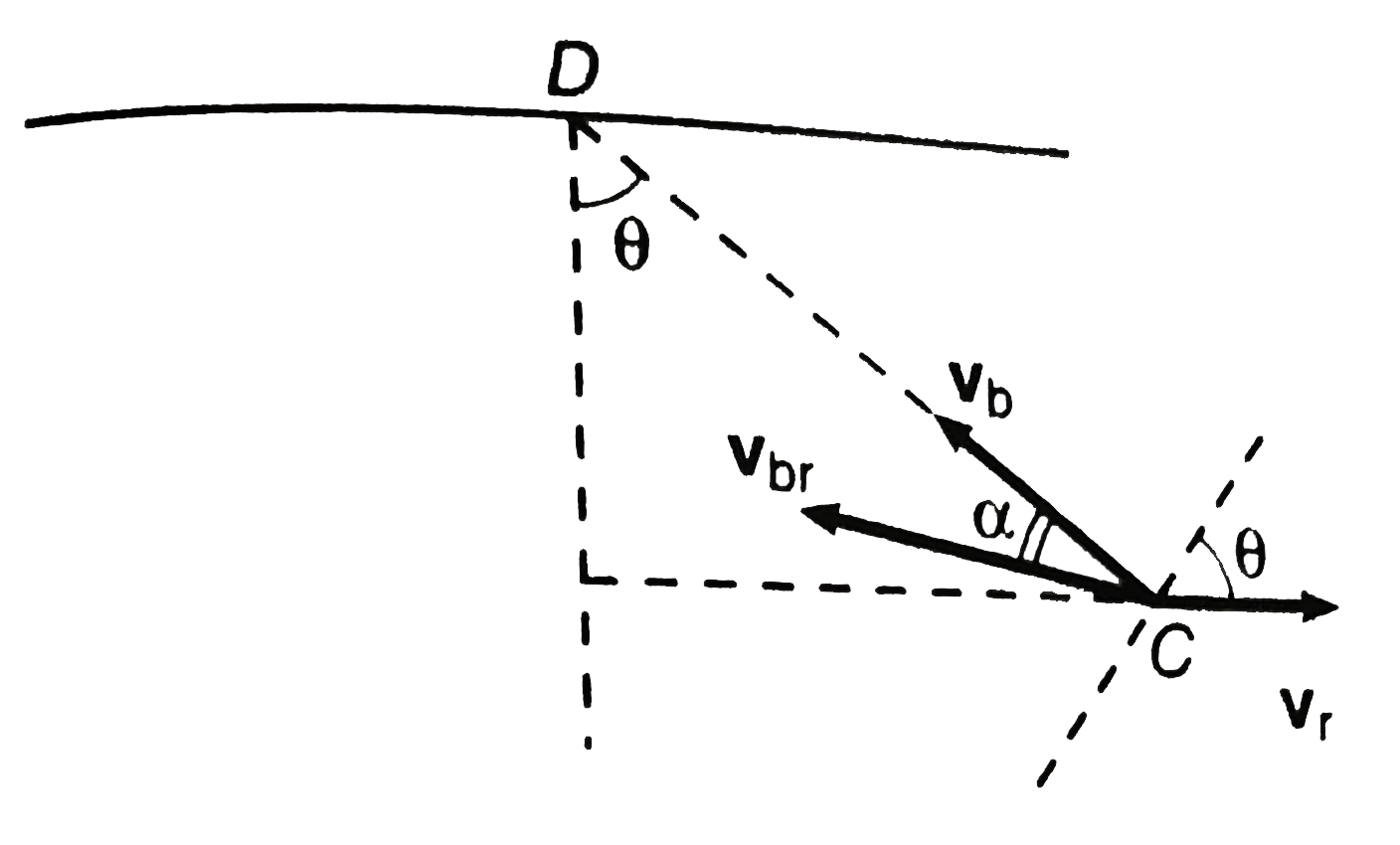
In this case, $v_{b}$ should be along CD.
$∴ V_{r} cos θ = v_{b r} sin α$

$2 (\frac{2}{\sqrt{5}}) = 4 sin α$
or $sin α = \frac{1}{\sqrt{5}}$
$∴ α = θ = {tan}^{- 1} (\frac{1}{2})$
(b) $t_{1} = \frac{200}{| v_{b r} |} = \frac{200}{4} = 50 s$
$D C = D B sec θ = (100) \frac{\sqrt{5}}{2} = 50 \sqrt{5} m$
$| v_{b} | = | v_{b r} | cos α - | v_{r} | sin θ$
$= 4 (\frac{2}{\sqrt{5}}) - 2 (\frac{1}{\sqrt{5}}) = \frac{6}{\sqrt{5}} m / s$
$∴ t_{2} = \frac{t_{1}}{2} + \frac{D C}{| v_{b} |} = 25 + \frac{50 \sqrt{5}}{\frac{6}{\sqrt{5}}} = \frac{200}{3} s$
or $\frac{t_{2}}{t_{1}} = \frac{4}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A river $500 m$ wide is flowing at a rate of $4 m / s .$ A boat is sailing at a velocity of $10 m / s$ with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
A $30 s$
B $40 s$
C $50 s$
D $60 s$
Question 2 - Select One
If speed of water in river is 4 m/s and speed of swimmer with respect to water is 3 m/s, then in which direction the swimmer must swim so that he will reach directly opposite end?
A $127^{\circ}$ with direction of river flow
B $60^{\circ}$ with direction of river flow
C $143^{\circ}$ with direction of river flow
DSwimmer will never reach directly opposite end
Question 3 - Select One
The velocity of a boat in still water is $10 m / s$ .If water flows in the river with a velocity of $6 m / s$ what is the difference in times taken to cross the river in the shortest path and the shortest time.The width of the river is $80 m$ .
A $1 s$
B $10 s$
C $\frac{\sqrt{3}}{2} s$
D $2 s$

DC PANDEY-KINEMATICS-Subjective Questions

Home
Ask Doubt
Profile