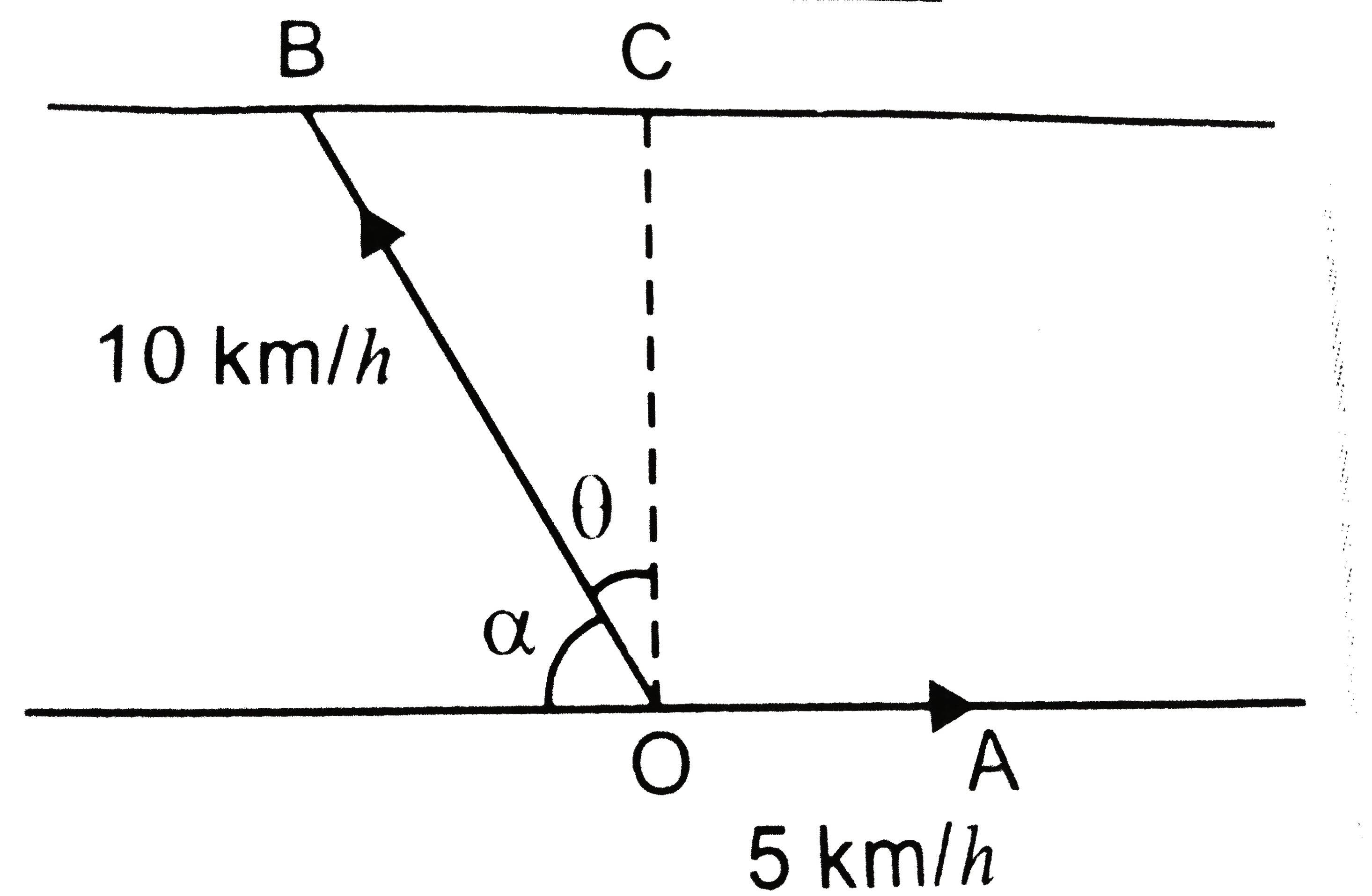
A boat man can rown with a speed of $10 k m h^{- 1}$ in still water. If the river flows steadily at $5 k m / h$ , in which direction showld the boatman row in order to reach a point on the other bank directly opposite to the point from wher he stared ? The width of the river is $2 k m$ .

Video Solution

Text Solution

Verified by Experts

Refer to Fig. 2 (c ) . 84. (b) , the velocity of river, $v_{r} = 5 k / m a l o n g$ (OA). The velocity of boatman, $v_{b} = 10 k m / h$ . The boatman can reach the other bank directly opposite to the point from where be has strated, if he goes along (OB) so that the resultant velocity may act along (OC).
.
Let $α$ be the angle which the boatman mades with upstream. Then. ltbRgt $θ + α = 90^{\circ}$ or theta = ( 90^@- alpha) $< b r > I n$ Delta OBC, sin theta = sin ( 90^@- alpha) $< b r >$ = cos alpha= (BC)/(OB)= 5/(10) = 1/2 cos 60^@ $< b r > or$ alpha = 60^@ upsteram.

Updated on:21/07/2023

A boat man can row with a speed of 10 km/hr. in still water. The river flow steadily at 5 km/hr. and the width of the river is 2 km. if the boat man cross the river with reference to minimum distance of approach then time elapsed in rowing the boat will be:-
A5.20 m
B4.33 m
C2.60 m
D8.66 m
A boatman can row with a speed of $10 k m h^{- 1}$ in still water. River flows at $6 k m h^{- 1}$ . If he crosses the river from one bank to the other along the shortest possible path, time taken to cross that river of width 1 km is
A $\frac{1}{8} h$
B $\frac{1}{4} h$
C $\frac{1}{2} h$
D $1 h$
The rowing speed of a man relative to water is $5 k m h^{- 1}$ and the speed of water flow is $3 k m h^{- 1}$ . At angle to the river flow should he head if he wants to reach a point on the other bank, directly opposite to starting point ?
A $127^{\circ}$
B $143^{\circ}$
C $120^{\circ}$
D $150^{\circ}$