A person standing on a road has to hold his umbrellat at $45^{\circ}$ with the vertical to deep the rain away . He throws the umbtella and starts running at $30 m s^{- 1}$ . He find that the rain drops are hitting his head vertically. Fing the speed of the rain drops with respect to (a) road (b) the moving person.

Video Solution

Text Solution

Verified by Experts

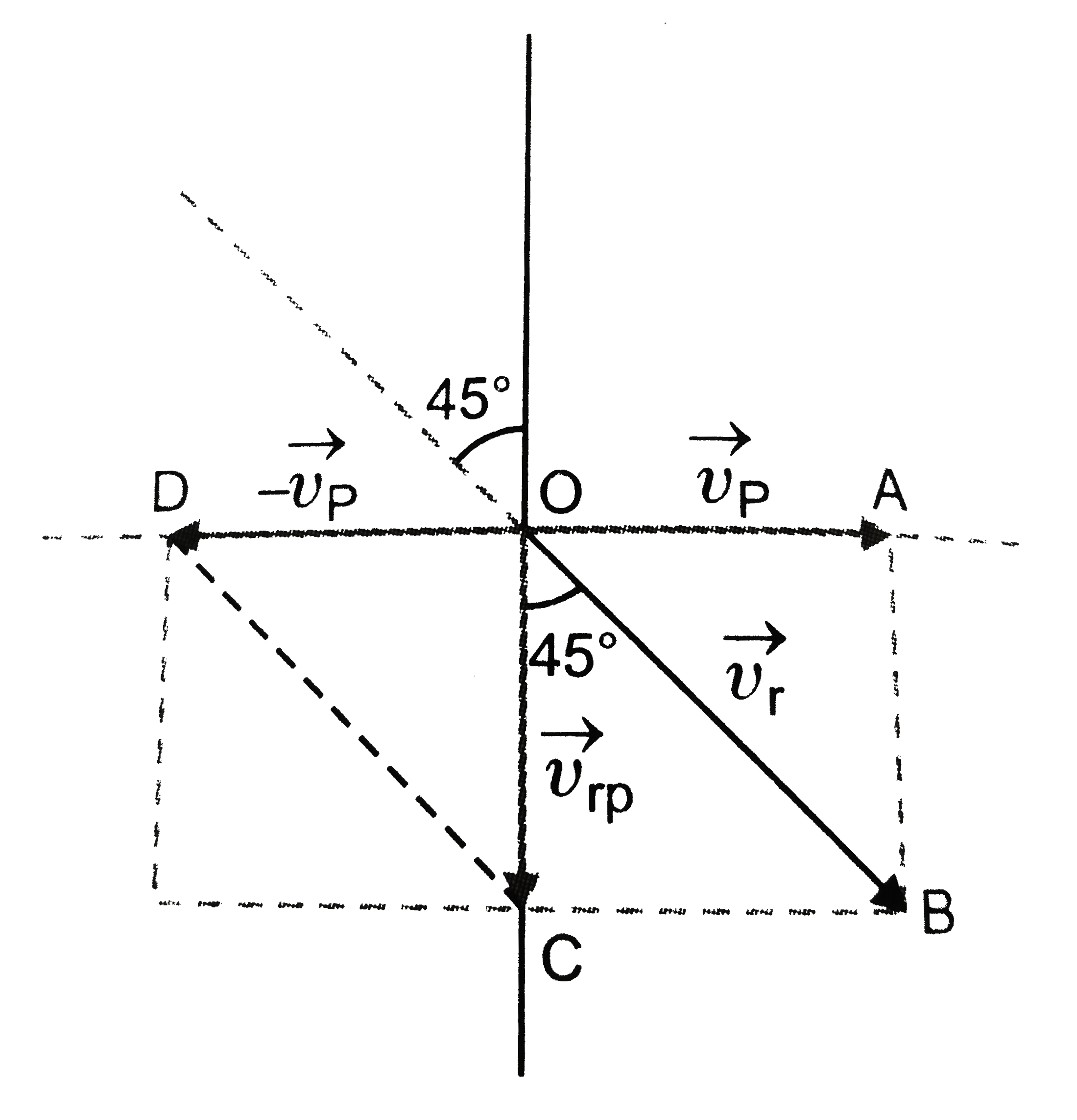
When person is at rest with respect to gorund, the rain is coming to him at an angle $45^{\circ}$ with the vertcal. i.e. Along (OB) . When a person a fter throwing his umbrella runs on ground at $30 m s^{- 1}$ , the relatve velcity of rain w.r.t. person , $v_{r p}$ is along (OC) as shown in Fig. 2 ( c) . 92. ltbRgt Here $∠ B O C = 45^{\circ}$
.
velocity of rain w.r.t. ground, $\to - - - r = - - \to O B$
volcity of person w.r.t. ground, ${\to v}_{P} = - - \to O B$ ltbRgt where $v_{P} = (O A) = 30 m s^{- 1} = C B$
velocity of fain w.r.t. person, ${\to v}_{r P} = - - \to O P$
In $Δ O C B$ , /_COB= 45^@ = /_OBC, so $O C = C B$ .
:. $v_{r P} = O C = 30 m s^{- 1}$
In $Δ O C B$ ,
$O B = \sqrt{O C^{2} + C B^{2}} = \sqrt{O C^{\circ} + O C^{2}}$ ltbRgt $= O C \sqrt{2} = 30 \sqrt{3} m s^{- 1}$
:. $v_{r} = 30 \sqrt{2} m s^{- 1}$ .

Updated on:21/07/2023

A man is running with a speed of 4 m/s, if he feels that rain drops are hitting him vertically with speed 3 m/s (along unit vector $- ˆ j$ ) then what can be the velocity of rain:
A $3 ˆ i - 4 ˆ j$
B $4 ˆ i + 3 ˆ j$
C $- 3 ˆ i - 4 ˆ j$
D $- 4 ˆ i - 3 ˆ j$
To a stationary man, rain appears to be falling at his back at an angle $30^{\circ}$ with the vertical. As he starts moving forward with a speed of $0.5 m s^{- 1}$ , he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
A $0.5 m s^{- 1}$
B $1.0 m s^{- 1}$
C $0.5 \sqrt{3} m s^{- 1}$
D $0.45 m s^{- 1}$
To a stationary man, rain appears to be falling at his back at an angle $30^{\circ}$ with the vertical. As he starts moving forward with a speed of $0.5 m s^{- 1}$ , he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
A $0.5 m s^{- 1}$
B $1.0 m s^{- 1}$
C $0.5 (\sqrt{3}) m s^{- 1}$
D $0.43 m s^{- 1}$