A box is thrown with velocity v0 on top of a rough table of length l. Assume friction on the object is such that during its motion, its acceleration is given as a=−kv, where k is a positive constant. Find the velocity of the box when it leaves the edge of the table. Also find the time after which it falls off the edge.
The correct Answer is:[v=v0−kl,t=1kln(v0v0−kl)]
Step by step video, text & image solution for A box is thrown with velocity v_(0) on top of a rough table of length l. Assume friction on the object is such that during its motion, its acceleration is given as a = -kv, where k is a positive constant. Find the velocity of the box when it leaves the edge of the table. Also find the time after which it falls off the edge. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Discussion Question
18 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Conceptual MCQs Single Option Correct
35 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
A body of mass m is thrown straight up with velocity v0(v0<<ve) Find the velocity v with which the body comes down if the air drag equals kv2, where k is a positive constant and v is the velocity of the body.
View SolutionThe acceleration. If v0 is themagnitude the engine is cut off, is given by dvdt=−kv2, wher (k) is a constant. If v0 is the magnitude of the velocity at cut off, find the magnitude of the velocity at time (t0 after the cut off.
View Solution
Knowledge Check
The deceleration exerienced by a moving motor blat, after its engine is cut-off is given by dv/dt=−kv3, where k is constant. If v0 is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time t after the cut-off is.
Av0/2BvCv0e−ktDv0√2v20kt+1The retardation experienced by a movign motr bat after its engine is cut-off , at the instant (t) is given by, =-k v^4,where(k)isaconstant.If v_0 is the magnitude of velocity at the cut-off , the magnitude fo velocity at time (t) after the cut-off is .
A(a) v_0 /(sqrt( 3 kt v_0^3)1B(b) v_0/(sqrt (3 kt v_0^3 + 1 ^(1//3))C(c ) sqrt ( 3 kt v_0^3)D(d) (3 kt v_0^3 + 1 )^(1//3)A uniform chain of length l is placed on a smooth horizontal table, such that half of its length hangs over one edge. It is releasedfrom rest, the velocity with which it leaves the table is
A√3gl4B√3gl2C√2gl3D√gl3
A body of mass m is thrown straight up with velocity v0. Find the velocity v′ with which the body comes down if the air drag equals kv3, where k is a constant and v is the velocity of the body.
View SolutionThe retadation experienced by a moving motor boat after its, engine is cutoff at the instant t is given by a=−kv4,where k is is a constant. If v0 is the magnitude of velocity at the cutoff, find the magnitude of velocity at time t after the cutoff.
View SolutionThe acceleration (a) of an object varies as a function of its velocity (v) as a=λ√v where λ is a constant.If at t=0,v=0, then the velocity as a function of time (t) is given as
View SolutionA projectile of mass m is fired into a liquid at an angle θ0 with an initial velocity v0 as shown. If the liquid develops a frictional or drag resistance on the projectile which is proportional to its velocity, i. e. F=−kv where k is a positive constant, determine the x and y components of its velocity at any instant. Also find the maximum distance xmax that it travels?
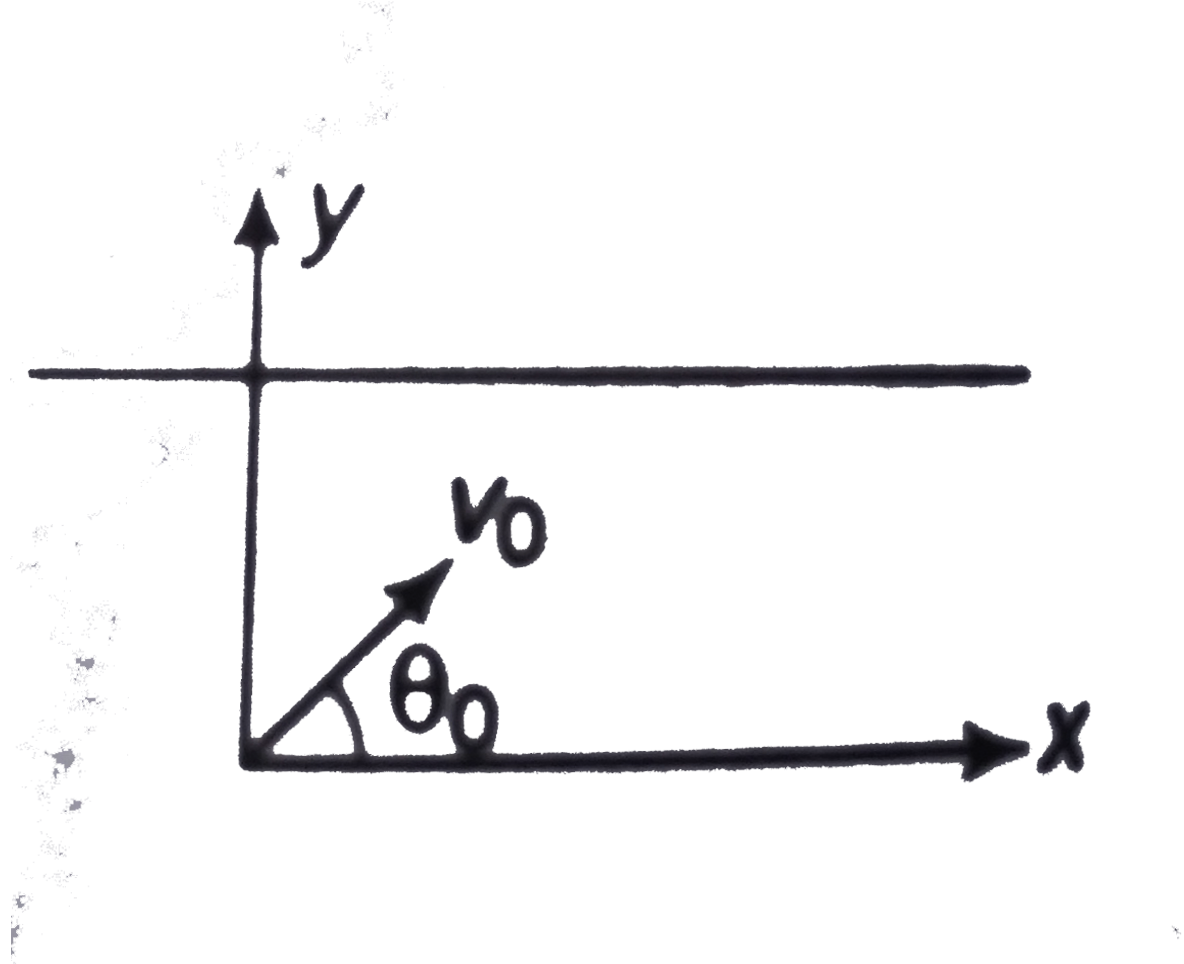
View SolutionA homogeneous chain of length 2l and mass M lies on an absolutely smooth table. A small part of the chain hangs from the table. At the initial moment, the part of the chain lying on the table is held and released, after which the chain begins to slide off the table under the weight of the hanging end. Find the velocity of the chain when the length of the hanging part is equal to x(x<I). Also calculate the acceleration and the force with which it acts on the edge of the table.
View Solution
