The body is rotating with uniform angular velocity (ω ) having rotational kinetic energy ( E) . Its angular momentum (L ) is :
2Eω
E2ω
Eω2
E2ω
The correct Answer is:A
Step by step video & text solution for The body is rotating with uniform angular velocity (omega ) having rotational kinetic energy ( E) . Its angular momentum (L ) is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JULY 2016Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: JULY 2016Exercise:SECTION -II
Explore 21 Videos
- FEBRUARY 2019Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: FEBRUARY 2019Exercise:SECTION-D
Explore 6 Videos
- JULY 2017Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: JULY 2017Exercise:SECTION-I
Explore 12 Videos
Similar Questions
Knowledge Check
Kinetic energy of rotation E and angular momentum L are related as
AE=L22IBE=2ILCE=√2ILDE=2√ILA rigid body rotates with an angular momentum L. If its rotational kinetic energy is made 4 times, its angular momentum will become
A4LB16LC√2LD2L
Two identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0. Change in the rotational kinetic energy of the system isAK0/2B−K0/2C−K0/4DK0/4
A rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
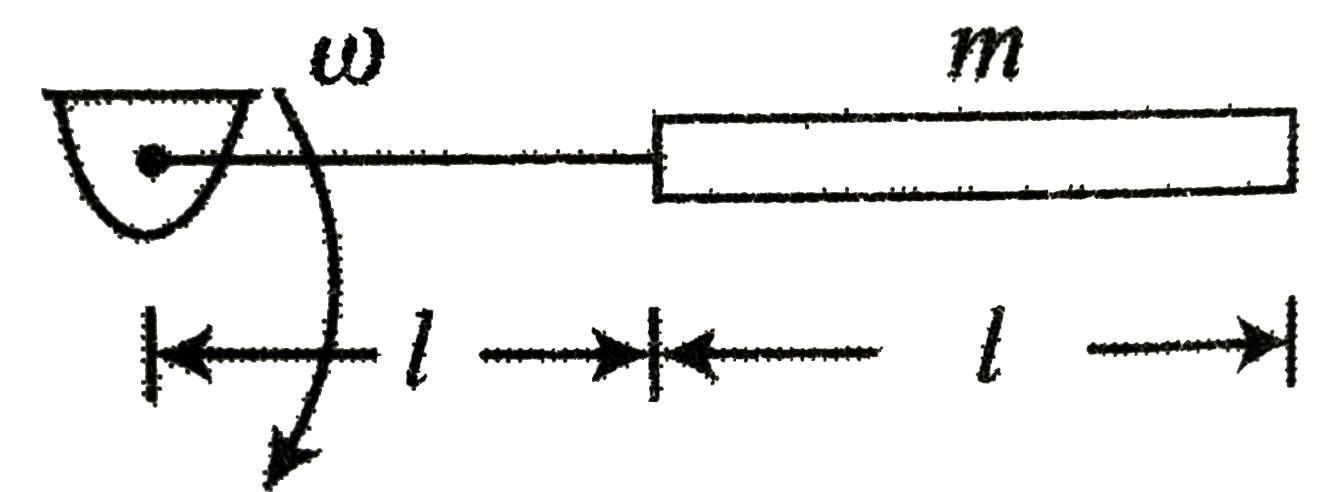
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionA heavy disc is rotating with uniform angular velocity ω about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
View SolutionA disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
View SolutionThe rotational kinetic energy of a body is E and its moment of inertia is I. The angular momentum is
View SolutionA uniform cylindrical rod of mass m and length L is rotating with an angular velocity ω. The axis of rotation is perpendicular to its axis of symmetry and passes through one of its edge faces. If the room temperature increases by t and the coefficient of linear expansion is α, the change in its angular velocity is
View Solution

