Using analytical method for interference bands, obtain an expression for path difference between two light waves.

Video Solution

Text Solution

Verified by Experts

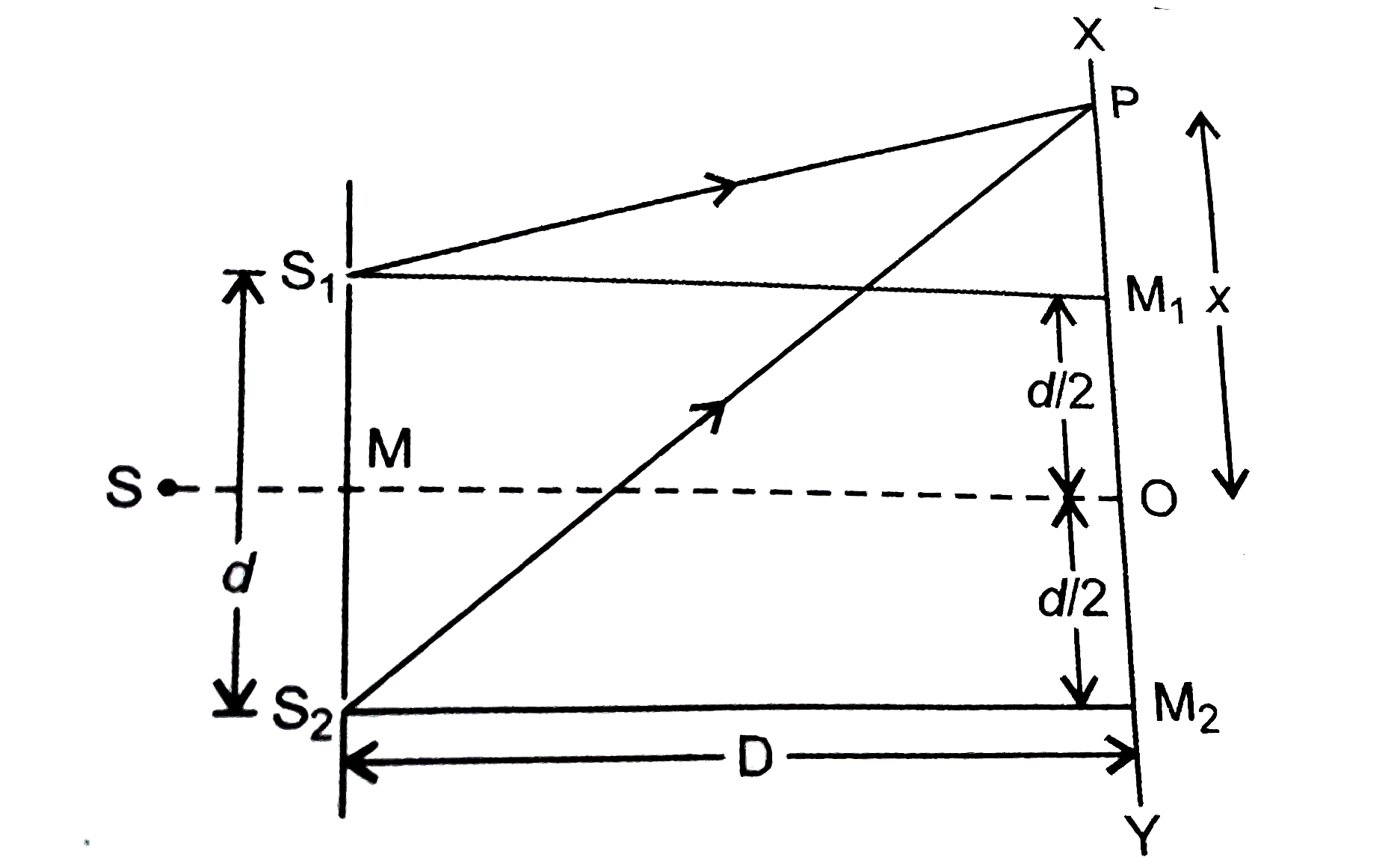
Consider S be narrow slit which is illuminated by monochromatic light of wavelength ( $λ$ ). $S_{1} and S_{2}$ are two parallel narrow slits which are separated by short distance d and are equidistant from S. the light waves from S will arrive at $S_{1} and S_{2}$ in the same phase. Beyond $S_{1} and S_{2}$ the waves will proceed as they had started from $S_{1} and S_{2}$ and will produce an interference pattern on the screen XY kept at distance D from the sources $S_{1} and S_{2}$ .

Theory of interference bands :
Let the perpendicular bisector OM of the line joning $S_{1} and S_{2}$ meet the screen at point O. since $S_{1} O = S_{2} O$ , the path difference between waves reaching O from $S_{1} and S_{2}$ is zero, therefore there is a bright point at O . The point O is called the centre of the interference pattern. suppose P be any point on the screen at distance x from O. The difference between the waves reaching P from $S_{1} and S_{2}$ is ( $S_{2} P - S_{1} P$ ) . suppose $S_{1} M_{1} and S_{2} M_{2}$ are perependiculars on the screen.
We have, $P M_{1} = x - \frac{d}{2} and P M_{2} = x + \frac{d}{2}$
In $Δ S_{2} M_{2} P$ ,
${(S_{2} P)}_{2}^{2} = {(S_{2} M_{2})}_{2}^{2} + {(P M_{2})}_{2}^{2}$
$∴ {(S_{2} P)}_{2}^{2} = D^{2} + {(x + \frac{d}{2})}^{2}$ ... (i)
In $Δ S_{1} M_{1} P$ ,
${(S_{1} P)}_{1}^{2} = {(S_{1} M_{1})}_{1}^{2} + {(P M_{1})}_{1}^{2}$
$∴ {(S_{1} P)}_{1}^{2} = D^{2} + {(x - \frac{d}{2})}^{2}$ ... (ii)
${(S_{2} P)}_{2}^{2} - {(S_{1} P)}_{1}^{2} = D^{2} + {(x + \frac{d}{2})}^{2} - D^{2} - {(x - \frac{d}{2})}^{2}$
$(S_{2} P - S_{1} P) (S_{2} P + S_{1} P) = x^{2} + x d + \frac{d^{2}}{4} - x^{2} + x d - \frac{d^{2}}{4}$
$∴ S_{2} P - S_{1} P = \frac{2 x d}{S_{2} P + S_{1} P}$
Now, the distance D is very large as compared to x and d.
$∴ S_{1} P = S_{2} P = D or S_{2} P + S_{1} P = 2 D$
Therefore , the path difference between two waves is given by
$S_{2} P - S_{1} P = \frac{2 x d}{2 D} = \frac{x d}{D}$

Updated on:21/07/2023

The path difference between two waves is
A $\frac{x D}{d}$
B $\frac{x d}{D}$
C $\frac{x D}{λ}$
D $\frac{x λ}{d}$
For destructive interference of sound waves the mathematical path difference between the two arriving waves is
A $n λ$
B $(2 n - 1) \times λ / 2$
Codd multiple of $π$
Deven multiple of $π$
In interference of light, a point is bright if the path difference between the two beams arriving at that point is
Aan integral multiple of the wavelengths
Ban odd multiple of the wavelengths
Can odd multiple of half of the wavelengths
Dan even multiple of half of the wavelengths