Show that even as well as odd harmonics are present as overtones in the case of an air column vibrating in a pipe open at both the ends.
A wheel of momen of intertia 1 kg m2 is rotating at a speed of 30 rad/s Due to friction on the axis, it comes to rest i n 10 mintes. Calculate the average torque of the friction.
Mode 1 : In this mode of vibration there is node at the centre of the pipe and two antionodes are at aeach open end
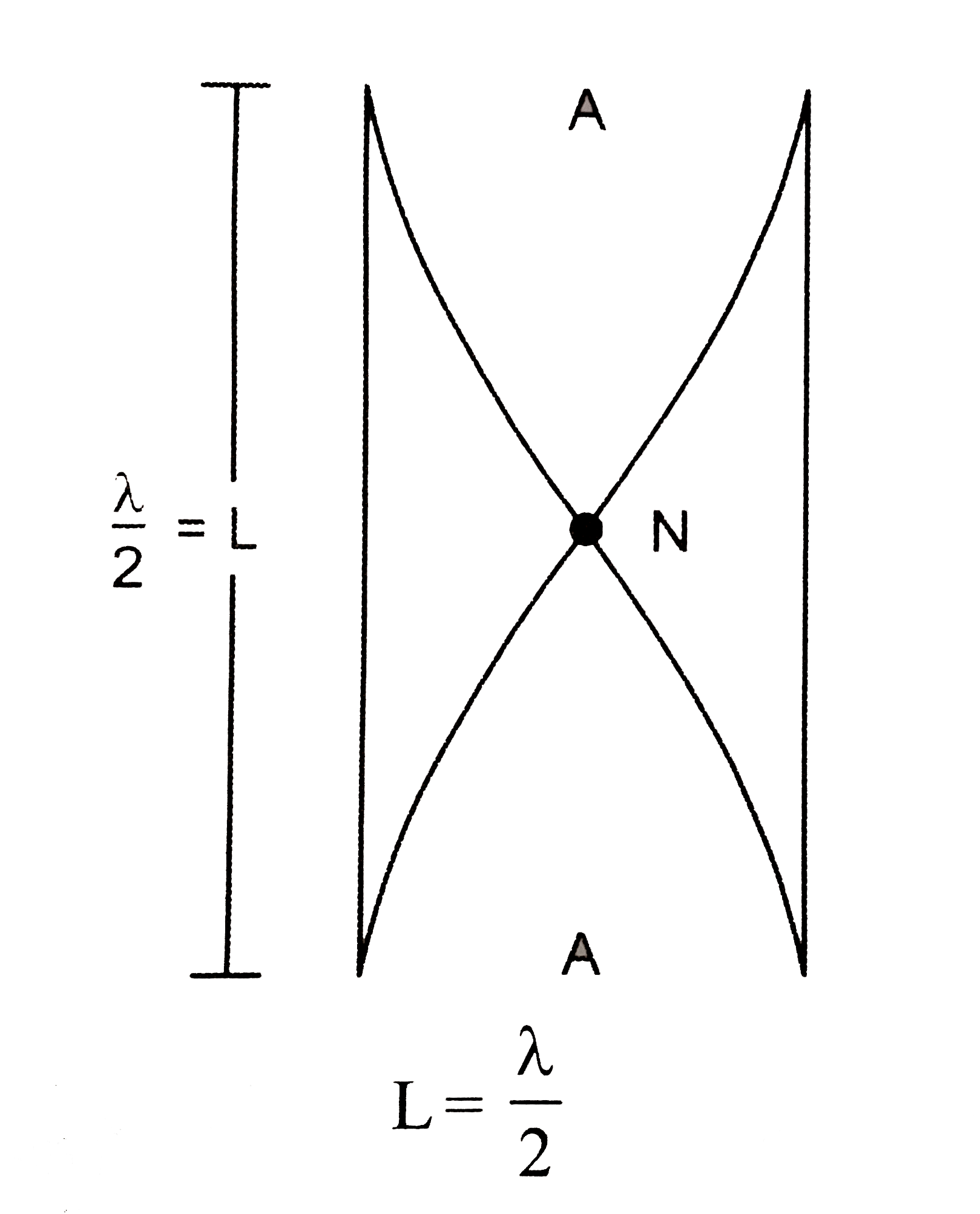
L=λ2
λ=2L
n=vλ
n=v2L
Fundamental frequency
n=[v2L]
Mode 2 : In this mode, there are three antinodes at top, bottom and centre having two intermediate nodes.
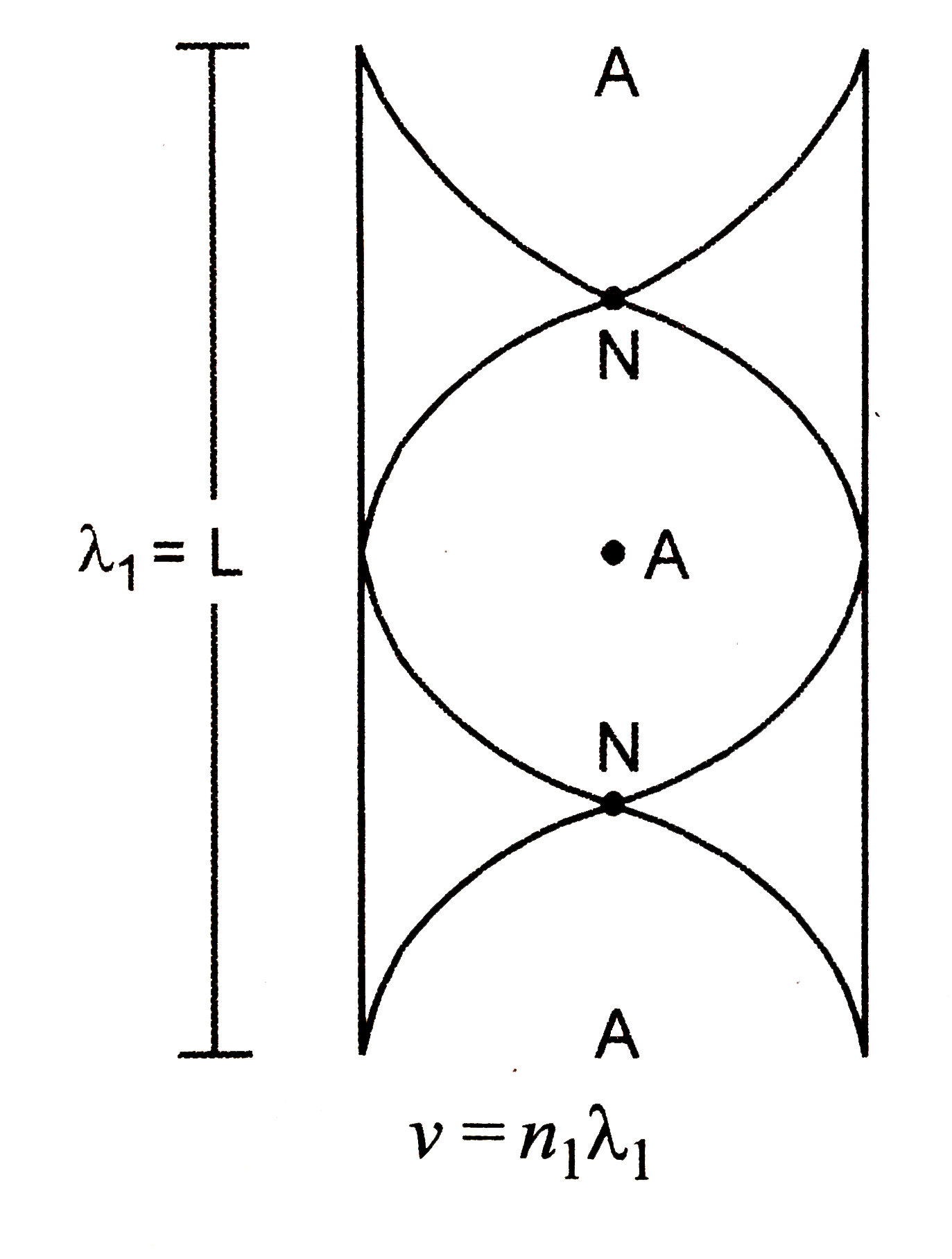
v=n1λ1
n1=vλ1
Also, λ1=L
n1=vL
∴n1=2(v2L)
∴n1=2n
Mode 3 : In this mode of vibration, there are 3 nodes and 4 antinodes.

v=n2λ2
n2=vλ2
n2=vλ2 (∴L=3λ22)
=3(v2L) ....(∴λ2=2L3)
∴n2=3n
∴ In general np=(p+1)n
or np=(p+1)v2L
where, p=1,2,3.....
From above expression it is clear that, In a tube which is open at both the ends all the harmonics are present as overtone
Numerical
Given I=kg,m2ω0=30 rad/sec ω=0
t=10min
=10×60=600sec
α=ω−ω0600
=−30600
α=−120rad/d2
τ=Iα
=1×−120
=−120
τ=−0.05Nm
Topper's Solved these Questions
- FEBRUARY 2019Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: FEBRUARY 2019Exercise:SECTION-C
Explore 12 Videos
- FEBRUARY 2018Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: FEBRUARY 2018Exercise:SECTION-II
Explore 21 Videos
- JULY 2016Book:GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSChapter: JULY 2016Exercise:SECTION -II
Explore 21 Videos
Similar Questions
A flywheel of moment of inertia 5.0kg−m2 is rotated at a speed of 10rad/s because of the friction at the axis it comes to rest in 10s. Find the average torque of the friction.
View SolutionWavelengths of two notes in air are (90175) m and (90173) m. Each note produces four beats per second with a third note of a fixed frequency. Calculate the velocity of sound in air.
View Solution
Knowledge Check
A whel of M.I. = 1kg−m2 is rotating at an angular speed of 40 rad/s. Due to friction on the axis, the wheel comes to rest in 10 minute. What is the angular momentum of the wheel inkgm2/s two minutes before it comes to rest ?
A3B5C6D8A wheel of moment of inertia 2kgm2 is rotating about an axis passing through centre and perpendicular to its plane at a speed 60rad/s. Due to friction, it comes to rest in 5 minutes. The angular momentum of the wheel three minutes before it stops rotating is
A24kgm2/sB48kgm2/sC72kgm2/sD96kgm2/sA flywheel of moment of inertia 3×102kgm2 is rotating with uniform angular speed of 4.6rads−1. If a torque of 6.9×102Nm retards the wheel, then the time in which the wheel comes to rest is
A1.5sB2sC0.5sD1s
A flywheel of moment of inertia 5.0 kg m^2 is rotated at a speed of 60 rad/s. Because of the frictionat te axle, it comes to rest in 5.0 minutes. Find a. The average torque of the friction. B. the total work done by the friction and c. the angular momentum of the wheel 1 minute before it stops rotating.
View SolutionA wheel of moment of inertia 3kgm2 rotates about an axis passing through its centre and perpendicular to its plane. Its initial speed of rotation is given as 60 rad /s. Due to friction, the wheel comes to rest in 5 minutes. If the angular momentum (in kg m2/s ) of the wheel three minutes before it stops is x then provide your answer as x100
View SolutionA fly wheel of moment of inertia 3×102 kg mạis rotating with uniform angular speed of 4.6 rad s−1. If a torque of 6.9×102 N m retards he wheel, then the time in which the wheel comes to rest is
View SolutionAn automobile moves on road with a speed of 54km/h. The radius of its wheel is 0.45m and the moment of inertia of the wheel about its axis of rotation is 3kgm2. If the vehicle is brought to rest in 15s, the magnitude of average torque transmitted by its brakes to the wheel is :
View SolutionAn automobile moves on a road with a speed of 54kmh−1 . The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m2 . If the vehicle is brought to rest in 15 s , the magnitude of average torque transmitted by its brakes to the wheel is
View Solution

